高压下LiNbO3晶体电子结构与光学性质的第一性原理研究

邵栋元, 程南璞, 陈志谦, 惠 群

(西南大学材料与能源学部， 重庆 400715)

高压下LiNbO3晶体电子结构与光学性质的第一性原理研究

邵栋元, 程南璞, 陈志谦, 惠 群

(西南大学材料与能源学部， 重庆 400715)

利用基于密度泛函理论的第一性原理超软赝势平面方法研究了外界压强对LiNbO3晶体态密度，能带结构，电荷密度以及光学性质的影响. 能带结构计算表明，价带顶主要由O-2p和Nb-4d态电子贡献，导带底主要由Nb-4d态电子贡献，且带隙随着压强的增加而线性增大. 利用复介电函数计算了LiNbO3晶体在不同压强下光学性质的折射率、反射率、吸收函数，能量损失函数以及光电导率. 研究发现：外界压强大于10 GPa时，静态折射率保持不变，随外界压强的增加，反射率、吸收函数以及光电导率区间有一定程度的拓宽，损失函数峰发生“蓝移”. 研究表明，外界高压可以有效调控LiNbO3晶体的电子结构和光学性质，为LiNbO3晶体的高压应用提供了有益的理论依据.

第一性原理; 电子结构; 光学性质

1 引 言

铌酸锂(LiNbO3)晶体是一种铁电材料，由于具有压电、电光、光折变性能和非线性光学特性，在传感器、过滤器、光学调制器、激光倍频器、光隔离器、全息存储器器件、光波导基片等光学器件方面获得了广泛的应用[1-3]，并且LiNbO3晶体具有较高声学波速度，可以作为很好薄膜材料和激光材料[4].

LiNbO3晶体具有良好的机械和物理性能，通过提拉法可以生长出高质量、大尺寸的LiNbO3单晶，在室温下呈铁电相，属于R3C空间群[5]. Liu通过化学方法制备了LiNbO3单晶，并测定了居里温度为1169 ℃[6]. 通过冲击压缩实验证明：压强33 GPa时，LiNbO3晶体发生相变，相应的体积会减小14%[7]，Lin等通过室温下的拉曼散射证明了压强为31 GPa时，LiNbO3晶体变为玻璃相，也称为非晶态[8]. Mukaide等证明，在室温下30 GPa的高压相被加热，仍然可以恢复到室温相，外界压强为35.6 GPa时LiNbO3晶体将发生完整的相变[9].

在光学研究领域，许多光学参量对材料的应用有重要的意义. M.Marsh等通过脉冲激光将LiNbO3沉积在α-Al2O3上，测定了LiNbO3的静态折射率为2.28[10]，Chaib建立了偶极子相互作用的微观模型[11]，计算了室温下LiNbO3晶体的电子结构和光学性质，其折射率(no=2.2824,ne=2.2282)与M.Marsh测得的值非常接近. Schlarb等测量了室温下不同元素掺杂LiNbO3的折射率，随着入射光波长增加，LiNbO3晶体折射率呈现减小趋势[12-14]. A.D.Redfield等测定LiNbO3晶体高温下的吸收率呈指数形式[15]，郑威等测定LiNbO3晶体吸收边为309 nm(3.79 eV)，以及红外透射光谱[16]，Hemet计算了铁电相LiNbO3的红外反射频谱[3]，师丽红等测定纯铌酸锂不同温度下的红外透射光谱和吸收光谱[17]，室温下LiNbO3晶体的透射率高达70%.综上述文献报道，LiNbO3晶体的光学性质只局限于静态光学参量和红外能量区域的研究，而缺乏全面的研究数据.

目前为止，对于LiNbO3晶体通过掺杂Fe、Mg、Ce、Mn、Cu等元素调控其带隙和光电性质的研究已有报道，但是通过施加压强调控LiNbO3光电性质的相关研究却未曾报道，本文将利用基于密度泛函理论的第一性原理方法，对高压下LiNbO3晶体的能带结构、态密度、折射率、反射率、吸收系数、能量损失函数、光电导率等光学性质进行了全面的计算，并对其变化规律做出系统的分析，希望对高压下LiNbO3晶体材料的应用提供一些有益的理论依据.

2 计算模型及方法

2.1 计算模型

LiNbO3晶体是一种畸变钙钛矿型结构，属三方晶系，其空间空群R3C，国际序号(No.161). 根据实验值[18]，晶格常数a=b=5.14 Å，c=13.86 Å，各原子坐标分别为Li(0, 0, 0.2802)，Nb(0, 0, 0)，O(0.0477, 0.3435, 0.0633). 图1为R3C理想LiNbO3晶体结构模型，晶胞中有6个Nb原子，6个Li原子，18个O原子.

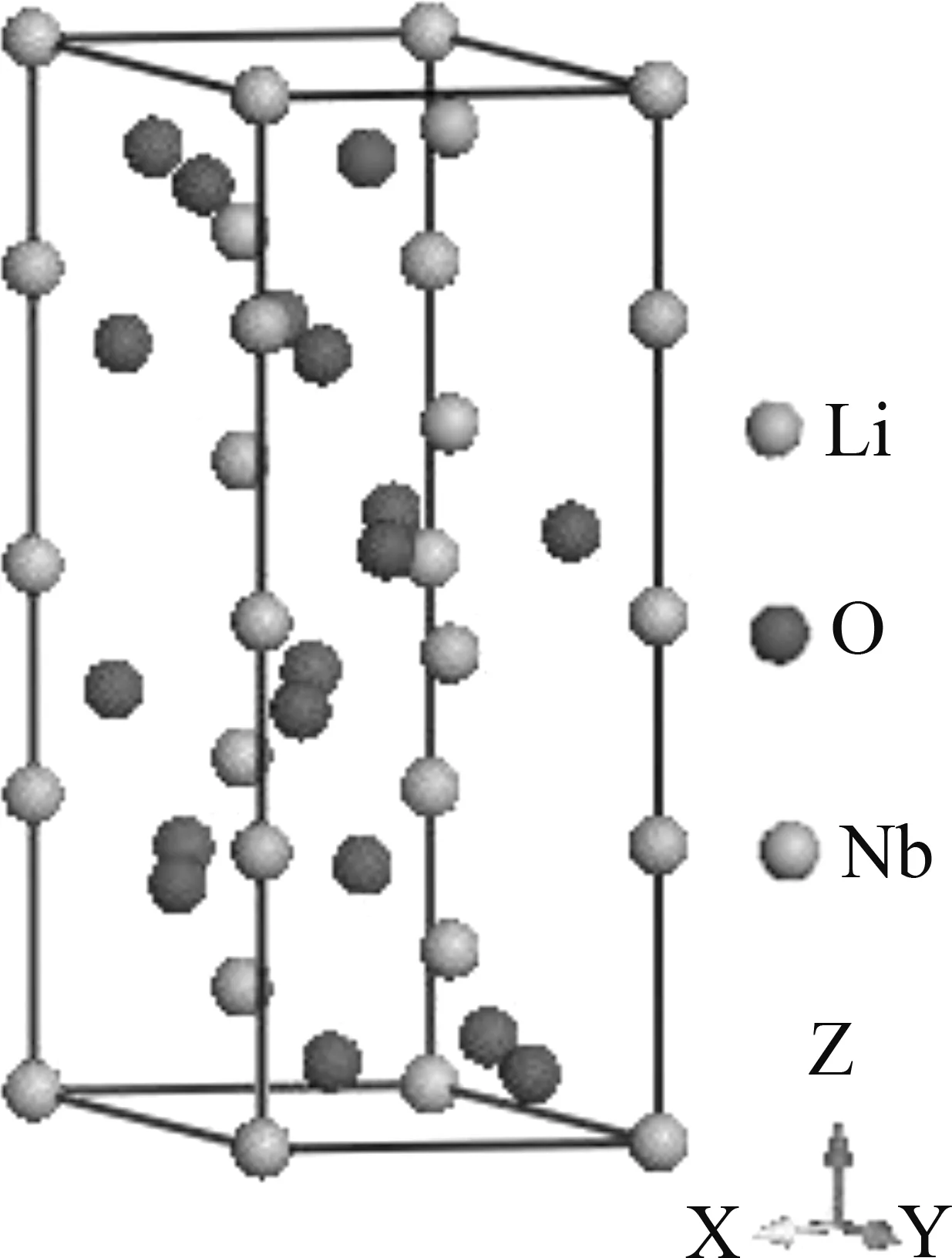
图1 LiNbO3晶体结构示意图Fig. 1 Schematic diagram of LiNbO3 crystal structure

2.2 计算方法

本文所有计算是基于密度泛函理论(DFT)的第一性原理方法，由CASTEP[19,20]模块计算完成.计算过程采用周期性边界条件，电子间的交换关联能采用广义梯度近似(GGA)[21]下的Perdew-Burke-Ernzerhof(PBE)方法[22]，晶体中电子的波函数由平面波基组展开，并由超软赝势(USPP)[23]实现离子实与价电子之间的相互作用势，原子的价电子组态分别为：Li为1s22s1，O为2s22p4，Nb为4s24p64d45s1. 波矢K空间中，平面波的截断能为300 eV，布里渊区积分采用3×3×2的Monkhorst-Pack[24]特殊K点对全布里渊区求和，运用Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法[25-28]，对晶体模型进行结构优化，当系统总能量变化稳定在0.2×10-5eV以内，并且使得优化后作用在晶胞中每个原子的应力小于0.53×10-2eV/Å，晶胞剩余应力低于0.05 GPa，公差偏移小于1.96×10-3Å时，视为达到收敛.

3 计算结果与讨论

3.1 几何结构优化

如表1所示，在没有外界压强的情况下，几何结构优化后的LiNbO3的晶格常数a(b)、c与实验测量值的相对误差分别为1.9%和2.5%，体系基本保持原来的结构，说明理论计算的结果准确度较高，本文采用的模型和计算方法合理可靠.

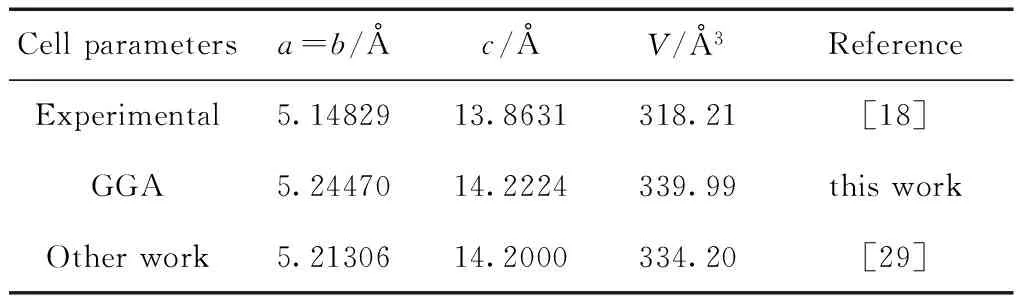
表1 LiNbO3晶体几何优化结果

3.2 静水压强对LiNbO3晶格常数的影响

如图2所示，随着压强由0 GPa增加到30 GPa，LiNbO3晶胞的体积和晶格常数均减小.在外界压强作用下LiNbO3晶体处于压缩状态，结构发生畸变，因此各原子间的相互作用力发生了变化，导致电子结构也发生变化. 在R3C-LiNbO3晶体结构优化的基础上，将具体的分析0 GPa、10 GPa、20 GPa、30 GPa静水压强对LiNbO3晶体电子结构和光学性质的影响.

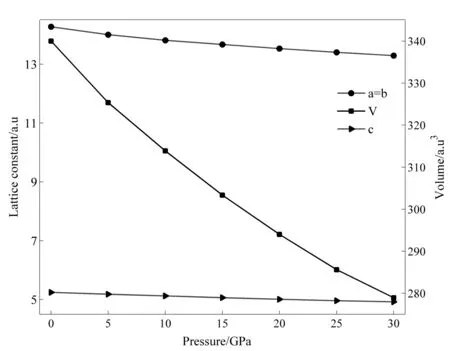
图2 不同压强下LiNbO3的晶格常数和晶胞体积Fig. 2 Lattice constants and crystall cell volume of LiNbO3 under different pressures

3.3 电子结构

图3为不同压强下LiNbO3晶体各原子的态密度分布情况，红色虚线表示费米能级. 压强为0 GPa时，在-55.28～-53.44 eV能量区间，由Nb-5s态电子贡献，-43.92～-41.89 eV能量区间，由Li-2s态电子贡献，-31.54～-29.48 eV能量区间，Nb-4p态电子贡献，-17.9～-14.1 eV能量区间，主要由O-2s态电子贡献，以及Nb-4p4d态电子的少量贡献，费米能级附近的价带-5.30～0 eV能量区间，主要由O-2p，Nb-4d态电子轨道组成. 导带部分2.63～5.76 eV能量区间，主要由Nb-4d态轨道组成. 导带和价带中分别存在部分的O-2p和Nb-4p4d态，这说明Nb-O间存在部分的共价键作用. 随着外界压强的增加，Li-2s电子能量峰值移向高能端，O-2s电子能量峰值减小，其余电子能量变化微弱. 图4为LiNbO3在不同压强下的能带结构，0 GPa时带隙为3.47 eV，比实验值3.78 eV偏小，其原因可能是LiNbO3是理想晶体，没有考虑杂质和温度的影响. 随着外界压强的增加，带隙逐渐增大，压强为30 GPa时，带隙增加为3.74 eV.

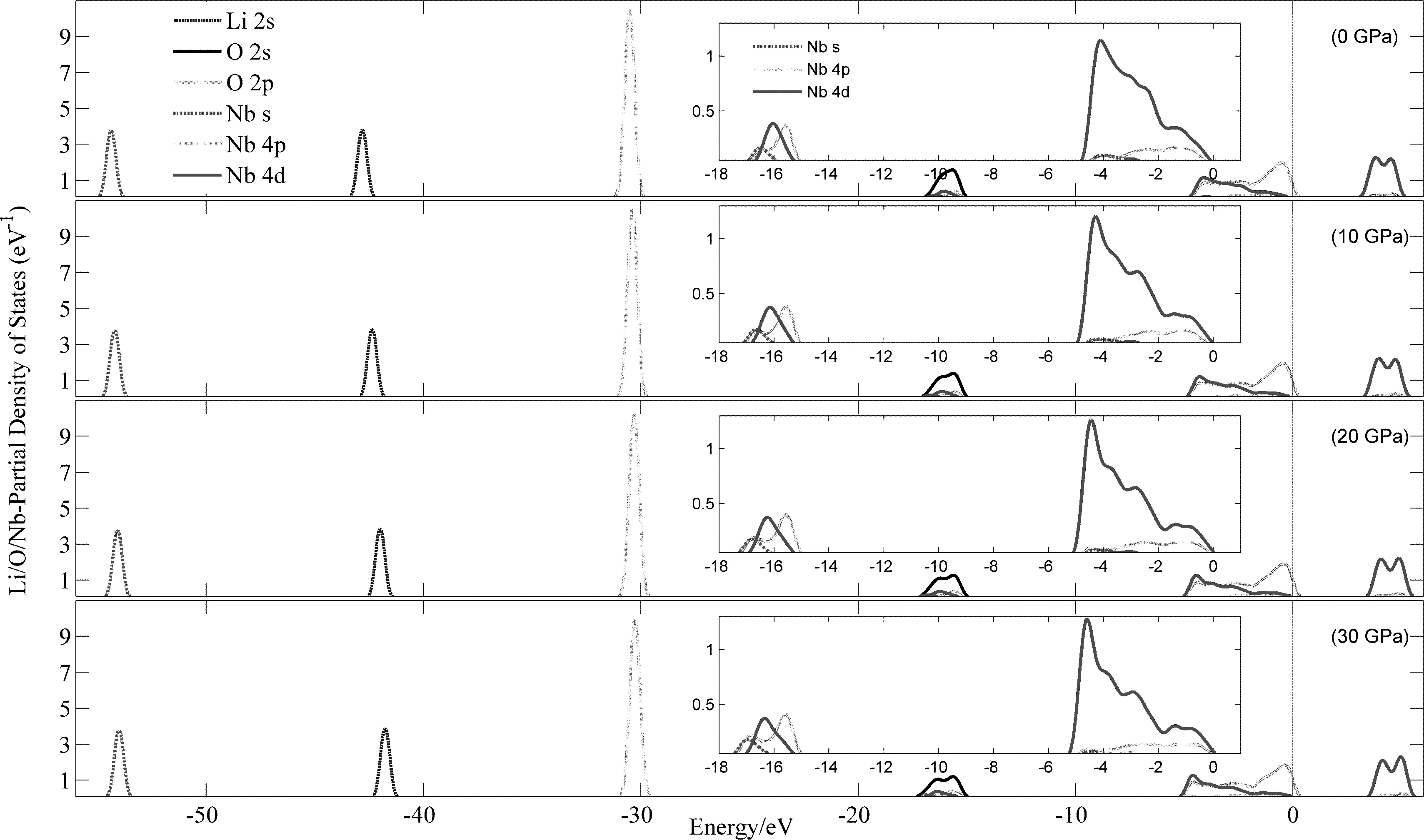
图3 不同压强下 LiNbO3晶体各原子的态密度Fig. 3 Density of states of LiNbO3 crystal under different pressures

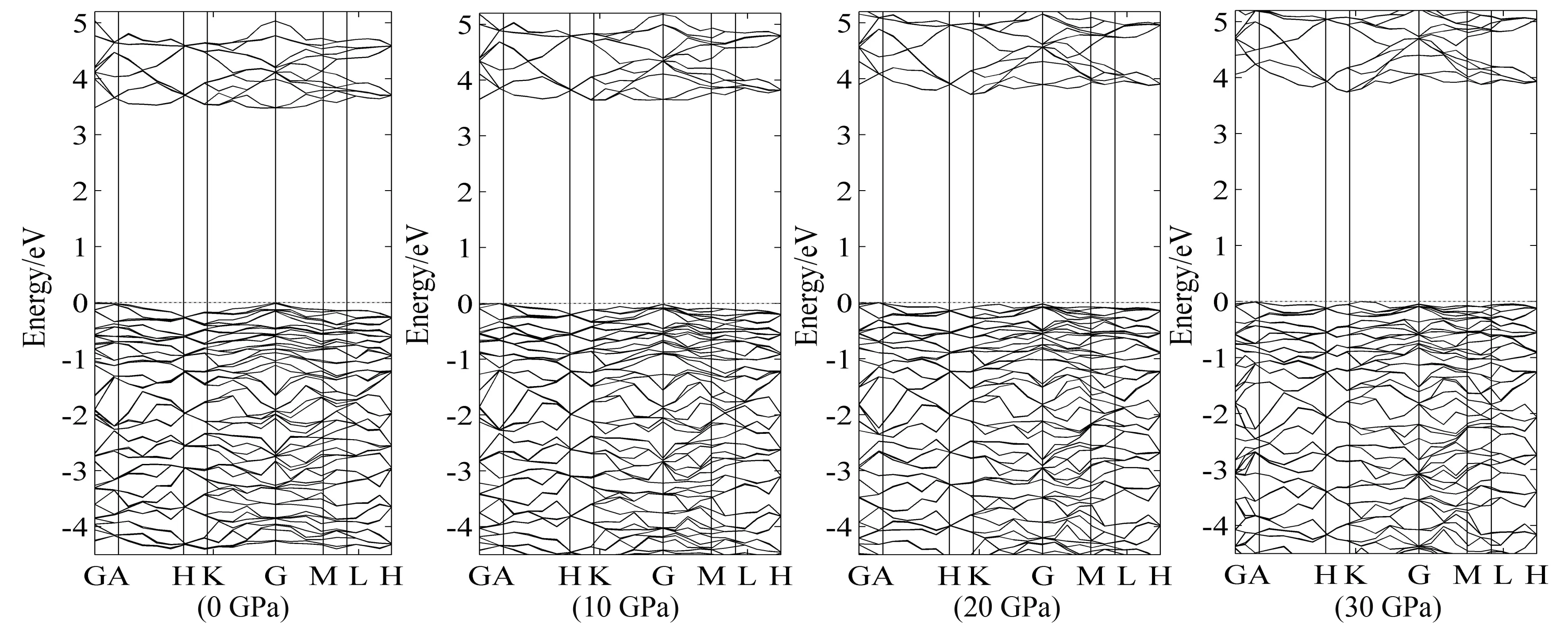
图4 不同压强下LiNbO3晶体的能带结构Fig. 4 Energy band structures of LiNbO3 under different pressures

3.4 布居分析与电荷密度图

为了直观地理解LiNbO3晶体各原子间的成键规律及相互作用，对晶胞中的电荷布居，各原子轨道电子占据数，键长和电子云重叠布居数进行了计算. 表2的计算结果表明：形成LiNbO3晶体主要的轨道贡献是Li的2s轨道，O的2p轨道和Nb的4p轨道，压强为0 GPa时，Li和Nb原子失去大部分价电子而带有+1.19和+1.10的正电荷，失去电子的能力较强，O原子带有-0.76的负电荷，得电子能力强. 电子云重叠布居数揭示O—Nb之间呈共价键，O—Li之间呈离子键. 随外界压强的增加，Li原子失去更多的电子，Nb原子失去更少的电子，O原子得到更多的电子，同时O—Nb、O—Li键长减小，O—Nb电子云重叠布居数增加，表明共价作用增强.

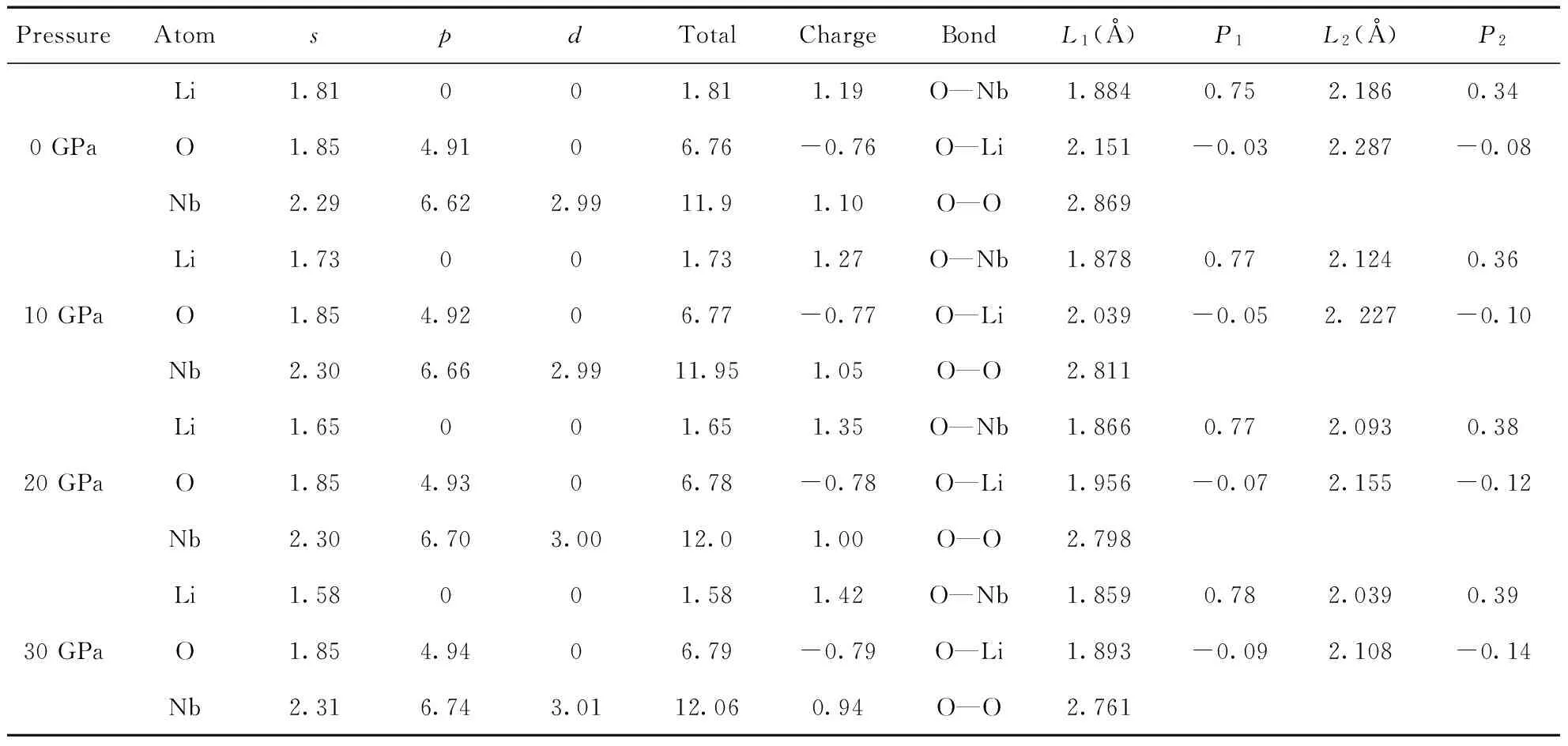
表2 不同压强下LiNbO3 晶体中各原子轨道电子占据数、各原子静电荷、键长L(Å)、电子云重叠布居P

图5为LiNbO3晶体(110)面电荷密度图，清楚的反映出各原子与周围原子的外层电子相互作用.图中黄色区域电子密度高，红色区域电子密度低，可以看出O原子周围电子密度低，Nb原子周围电子密度高，Nb原子的轨道和O原子的轨道有很强的重叠，形成强共价键，与态密度及电子云重叠布居数分析的结果一致，随着压强的增加，Nb原子外层电子作用范围增加，与周围的O原子外层电子作用加剧，电子跃迁更加频繁. Li原子周围电子密度较低，且作用范围较小，随压强的增加，外层电子作用范围也增加，原子中心偏向周围的O原子，导致O—Li键键长减小，其结果与布居分析相一致.

图5 LiNbO3在不同压强下(110)面电荷密度Fig. 5 (110) plane contour charge density of LiNbO3 under different pressures

3.5 光学性质分析

线性响应范围内，固体宏观光学响应函数通常由光的复介电常数ε(ω)=ε1(ω)+iε2(ω)来描述，其中

ε1=n2-k2,

(1)

ε2=2nk,

(2)

其中n和k分别为折射和消光系数. 根据直接跃迁几率的定义和Kramers-Kroing色散关系得到介电函数的实部与虚部[30]

δ[EC(k)-EV(k)-ħω],

(3)

(4)

其中m为自由电子质量，e为自由电子电量，ω为入射光子频率，C代表导带，V代表价带，EC(K)为导带上的本征能级，EV(K)为价带上的本征能级，BZ代表第一布里渊区，K是倒格矢，|eMCV(K)|2是动量跃迁矩阵元. 进而推导出其他光学常数，包括折射率，反射率，吸收率和能量损失函数等.在这里我们讨论高压对LiNbO3光学常数的影响.

图6为LiNbO3在不同压强下的折射率随能量的变化曲线，压强为0 GPa时LiNbO3的静态折射率为1.88，光子能量为3.91 eV时，折射率达到最大值，压强大于10 GPa时，静态折射率几乎保持不变. 随着压强的增加，折射率的所有峰值均移向高能端，入射光能量大于45 eV时，不同压强下的折射率逐渐重合并趋于定值.

图6 LiNbO3在不同压强下的折射率Fig. 6 Refrative indexs of LiNbO3 under different pressures

图7为LiNbO3在不同压强下的反射率随能量变化的曲线，压强为0 GPa，能量为9.3 eV时，反射率达到峰值，外界压强由0 GPa增加到30 GPa时，反射率峰值由0.77增加为0.89，反射率峰值向高能端移动1.3 eV，随着入射光能量的增加，反射率达到第一个峰值后急剧下降，随着压强的增加，并且反射区间向高能端拓宽. 入射光能量为35.7 eV时出现第二个较大的峰，随压强的增加，反射区间向高能区拓宽，反射率峰值增加，入射光能量大于40 eV时，不同压强下的反射率逐渐趋于零.

图7 LiNbO3在不同压强下的反射率Fig. 7 Reflectivities of LiNbO3 under different pressures

晶体中每一种原子都有固定的振动频率，当入射光波段的频率和晶体原子的固有频率一致时，就会引起共振吸收，入射光能量强烈的被吸收. 图8为LiNbO3在不同压强下的吸收函数随能量变化曲线，由图可知，LiNbO3晶体的光吸收边为3.04 eV，比文献值低[16]. 压强0 GPa时，能量为5.5 eV，吸收函数达到峰值，吸收谱宽度约为7 eV. 随外界压强的增加，在18～23 eV、33～37 eV能量区间，吸收函数均向高能区拓宽，在45.2～48.5 eV能量区间，吸收函数向低能区拓宽，峰值均增加，这是由于压强的增加，晶体中原子的固有振动频率增加，因而吸收范围拓宽.

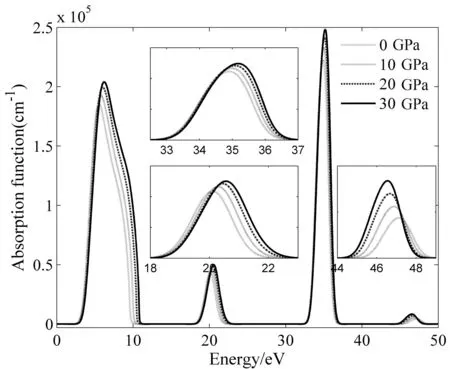
图8 LiNbO3在不同压强下的吸收函数Fig. 8 Absorption functions of LiNbO3 under different pressures

能量损失函数描述了电子穿过均匀介质造成的能量损失，理论上电子能量损失谱定义为复介电函数的倒虚部[30]. 图9为LiNbO3晶体在不同压强下的能量损失函数曲线，压强为0 GPa时，入射光能量为9.57 eV时，损失峰值为46.60，外界压强增加为30 GPa时，共振能量为10.81 eV时，损失函数峰值增加为135.20，并且移向高能端. 能量在18～23 eV范围时，有一个比较小的损失峰，随着压强的增加，损失范围向高能端拓宽，峰值也移向高能端.LiNbO3晶体对光的损失只局限于特定的能量范围，因此LiNbO3晶体可以作为较好的光存储材料.

图9 LiNbO3在不同压强下能量损失函数Fig. 9 Energy loss functions of LiNbO3 under different pressures

光电导率体现了材料对不同能量光子的吸收对其电导率的影响.图10为LiNbO3在不同压强下的光电导率随能量的变化曲线，压强为0 GPa时，入射光的能量小于2.8 eV时，光电导率趋于零，这是由于费米能级以上没有自由电子. 入射光能量大于2.8 eV时，光电导率迅速增加，压强由0 GPa增加为30 GPa时，光电导率的第一个峰值由5.1增加为5.6. 入射光能量在18.3～22.5 eV、33～36.8 eV光电导率向高能区拓宽，在45.2～48.5 eV光电导率向低能区拓宽，峰值均有少许增加，外界压强的增加，对光电导率的影响非常微弱.

图10 LiNbO3不同压强下的光电导率Fig. 10 Conductivities of LiNbO3 under different pressures

4 结 论

本文利用基于第一性原理的密度泛函理论下的广义梯度近似方法(GGA)，对LiNbO3晶体不同压强下的电子结构与光学性质进行了计算. 随着外界压强的增加，LiNbO3晶体的晶格常数和晶胞体积逐渐减小，而带隙呈现增加趋势. 通过对Li、O、Nb原子的态密度进行了分析，随着外界压强的增加，Li-2s态电子能量峰值移向高能端，而O-2s态电子能量峰值降低，Nb-4d态电子和O-2p态电子的作用增强，杂化加剧. 借助复介电函数对光学性质进行了系统的分析，压强大于10 GPa时，静态折射率几乎保持不变，然而折射率峰值均增加，并且峰值均移向高能端，随压强的增加，反射率区间均有一定程度的拓宽，峰值也有稍许的增加，吸收率峰值增加，吸收能量区间有一定的拓宽.外界压强为30 GPa时损失函数峰值增加为0 GPa的3倍，损失函数峰值产生“蓝移”，光电导率随外界压强的增加有一定程度的拓宽，峰值几乎保持不变. 因此施加压强可以有效调制LiNbO3晶体的电子结构，也是改变光学性能的有效手段.

[1] Korkishko Y N, Fedorov V A, Kostritskii S M,etal. Proton exchanged LiNbO3and LiTaO3optical waveguides and integrated optic devices [J].MicroelectronicEngineering, 2003, 69(2): 228.

[2] Xue D, Betzler K. Influence of optical-damage-resistant dopants on the nonlinear optical properties of lithium niobate [J].Appl.Phys. B, 2001, 72(6): 641.

[3] Hermet P, Veithen M, Ghosez P. First-principles calculations of the nonlinear optical susceptibilities and Raman scattering spectra of lithium niobate [J].Phys. B:CondensedMatter, 2007, 19(45): 456202.

[4] Kushibiki J, Takanaga I, Arakawa M,etal. Accurate measurements of the acoustical physical constants of LiNbO3and LiTaO3single crystals [J].IEEETransactionsonUltrasonics,FerroelectricsandFrequencyControl, 1999, 46(5): 1315.

[5] He X K, Xue D F. Defect and control lithium niobate crysrals [J].JournalofSyntheticCrystals., 2006, 34(5): 884 (in Chinese) [贺祥珂, 薛冬峰. 铌酸锂晶体的缺陷及其控制 [J]. 人工晶体学报, 2006, 34(5): 884]

[6] Liu M, Xue D, Li K. Soft-chemistry synthesis of LiNbO3crystallites [J].J.AlloysCompd., 2008, 449(1): 28.

[7] Goto T, Syono Y. Shock-induced phase transformation in lithium niobate [J].J.Appl.Phys., 1985, 58(7): 2548.

[8] Lin Y, Li Y, Xu Y,etal. Raman-scattering study on pressure amorphization of LiNbO3crystal [J].J.Appl.Phys., 1995, 77(7): 3584.

[9] Mukaide T, Yagi T, Miyajima N,etal. High pressure and high temperature phase transformations in LiNbO3[J].J.Appl.Phys., 2003, 93(7): 3852.

[10] Marsh A M, Harkness S D, Qian F,etal. Pulsed laser deposition of high quality LiNbO3films on sapphire substrates [J].Appl.Phys.Lett., 1993, 62(9): 952.

[11] Chaib H, Otto T, Eng L M. Electrical and optical properties of LiNbO3single crystals at room temperature [J].Phys.Rev. B, 2003, 67(17): 174109.

[12] Schlarb U, Wöhlecke M, Gather B,etal. Refractive indices of Zn-doped lithium niobate [J].OpticsMaterials, 1995, 4(6): 791.

[13] Kasemir K, Betzler K, Matzas B,etal. Influence of In doping on the refractive indices of lithium niobate [J].PhysicaStatusSolidiA, 1998, 166(1): R7.

[14] Sun L, Guo F, Lv Q,etal. Increased optical damage resistance of Zr:LiNbO3crystals [J].CrystalResearchandTechnology, 2007, 42(11): 1117.

[15] Redfield D, Burke W J. Optical absorption edge of LiNbO3[J].J.Appl.Phys., 1974, 45(10): 4566.

[16] Zheng W, Wang F C, Xu Y H. Growth and structure of near-stoichiometric lithium niobate crystal [J].JournaloftheChineseCeramicSociety, 2005, 32(11): 1367 (in Chinese) [郑威, 王凤春, 徐玉恒. 近化学计量比铌酸锂晶体的生长及其结构 [J]. 硅酸盐学报, 2005, 32(11): 1367]

[17] Shi L H, Yan W B. Study on infrared absorption spectra of congruent lithium niobate crystals at low temperature [J].ActaPhys.Sin., 2009, 58(7): 4987 (in Chinese) [师丽红, 阎文博. 纯铌酸锂晶体红外光谱的低温研究 [J]. 物理学报, 2009, 58(7): 4987]

[18] Abrahams S C, Hamilton W C, Reddy J M. Ferroelectric lithium niobate. 4. Single crystal neutron diffraction study at 24 ℃ [J].Phys.Chem.Solids, 1966, 27(6): 1013.

[19] Payne M C, Teter M P, Allan D C,etal. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients [J].Rev.Mod.Phys., 1992, 64(4): 1045.

[20] Milman V, Winkler B, White J A,etal. Electronic structure, properties, and phase stability of inorganic crystals: A pseudopotential plane-wave study [J].Int.J.QuantumChem., 2000, 77(5): 895.

[21] Hammer B, Hansen L B, Norskov J K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals [J].Phys.Rev. B, 1999, 59(11): 7413.

[22] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple [J].Phys.RevLett., 1996, 77(18): 3865.

[23] Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J].Phys.Rev. B, 1990, 41(11): 7892.

[24] Monkhorst H J, Pack J D. Special points for Brillouin-zone integrations [J].Phys.Rev. B, 1976, 13(12): 5188.

[25] Broyden C G. The convergence of a class of double-rank minimization algorithms 2. the new algorithm [J].J.Inst.Math.Appl., 1970, 6(3): 222.

[26] Fletcher R. A new approach to variable metric algorithms [J].Comput.J., 1970, 13(3): 317.

[27] Goldfarb D. A family of variable-metric methods derived by variational means [J].Math.Comput., 1970, 24(109): 23.

[28] Shanno D F. Conditioning of quasi-Newton methods for function minimization [J].Math.Comput., 1970, 24(111): 647.

[29] Lei X W, Lin Z, Zhao H. First principles study of Mn-doped LiNbO3[J].J.At.Mol.Phys., 2010, 27(5): 1005 (in Chinese) [雷晓蔚, 林竹, 赵辉. 掺锰铌酸锂晶体第一性原理研究 [J]. 原子与分子物理学报, 2010, 27(5): 1005]

[30] Duan M Y, Xu M, Zhou H P,etal. Frist-principle on the electronic structure and optical properties of ZnO doped with transition metal and N [J].ActaPhys.Sin., 2007, 56(9): 5359 (in Chinese) [段满益, 徐明, 周海平, 等. 过渡金属与氮共掺杂ZnO电子结构和光学性质的第一性原理研究 [J]. 物理学报, 2007, 56(9): 5359]

First-principles studies electronic structures and optical properties of LiNbO3under high pressure

SHAO Dong-Yuan， CHENG Nan-Pu， CHEN Zhi-Qian， HUI Qun

(Faculty of Material and Energy, Southwest University, Chongqing 400715, China)

The effects of the external pressure on the density of states, band structure, charge density and optical properties of lithium niobate are investigated with the plane wave psuedopetential method based on the first-principles density functional theory. It is found that the top of the valence band is mainly determined by the orbital electrons of O-2p and Nb-4d, and the band gap presents a linear increased trend with the increasing external pressure. Moreover, the refractive index, the reflectivity, absorption function, the energy loss function and the conductivity of optical properties of the lithium niobate crystal are calculated by the complex dielectric function under different pressures. The results show that when the external pressure is greater than 10 GPa, the static refractive index remains constant, and the variation ranges of the reflectivity rate, the absorption function and the conductivity rate are widened with the increasing external pressure. The peaks of energy loss function exhibit blue shift with the increasing external pressure. Our results show that the electronic structures and optical properties of LiNbO3can be effectively modulated by changing external high pressure, which provides a useful theoretical basis for the further application of the lithium niobate crystal under high pressure.

First-principles; Electronic structure; Optical properties

103969/j.issn.1000-0364.2015.12.031

2014-09-25

国家自然科学基金(51171156) ; 西南大学博士基金(SWUB2007018)

邵栋元(1988—),男，甘肃人,硕士研究生，主要研究方向为材料物理与化学.E-mail: sdy1988719@swu.edu.cn

惠群.E-mail: qhui01@swu.edu.cn

O521; O481

A

1000-0364(2015)06-1097-08