(110)应变对立方相Ca2P0.25Si0.75能带结构及光学性质的影响
岑伟富, 杨吟野, 范梦慧, 姚 娟, 杨文帮, 黄金保
(贵州民族大学理学院, 贵阳 550025)
(110)应变对立方相Ca2P0.25Si0.75能带结构及光学性质的影响
岑伟富, 杨吟野, 范梦慧, 姚 娟, 杨文帮, 黄金保
(贵州民族大学理学院, 贵阳 550025)
采用第一性原理贋势平面波方法对(110)应变下立方相Ca2P0.25Si0.75的能带结构及光学性质进行模拟计算,全面分析了应变对Ca2P0.25Si0.75能带结构、光学性质的影响.计算结果表明:在92%~100%压应变范围内随着应变的逐渐增大导带向低能方向移动,价带向高能方向移动,带隙呈线性逐渐减小,但始终为直接带隙;在100%~102%张应变范围内随着应变的增加,带隙呈逐渐增大,应变达到102%直接带隙最大Eg=0.54378 eV;在102%~104%应变范围内随着应变的增加,带隙逐渐减小;当应变大于104%带隙变为间接带隙且带隙随着应变增大而减小.施加应变Ca2P0.25Si0.75的介电常数、折射率均增大;施加压应变吸收系数增加,反射率减小;施加张应变吸收系数减小,反射率增加.综上所述,应变可以改变Ca2P0.25Si0.75的电子结构和光学常数,是调节Ca2P0.25Si0.75光电传输性能的有效手段.
应变; 光学性质; 能带结构; 第一性原理; Ca2P0.25Si0.75
1 引 言
碱土金属硅化物Ca-Si是一种新型的环境友好型半导体材料,Ca和Si反应生成六个中间相,其中Ca2Si是直接迁移型半导体.Ca2Si具有两种结构,一种属于正交晶系,为稳定结构[1],禁带宽度为0.36 eV,与实验值1.9 eV相差较大[2,3];另一种结构属于立方晶系,在外压力作用下为稳定结构,禁带宽度为0.56 eV[4].Ca2Si具有优异的光学、电学性质,同时能在硅基上外延生长,在制备和使用过程中对环境无污染长期使用对生命体无害,因此在光电子器件、电子器件及热电器件等领域有广泛的应用前景,是一种潜在的理想半导体材料.目前,国内外对其研究投入大量的人力、财力. 如Imai等[2,5]利用第一性原理贋势方法(The first-principle pseudo potential method)计算得出正交相Ca2Si的能带结构,带隙为0.36 eV的直接带隙半导体. Migas等[6]用全电势线性化缀加平面波方法(FLAPW)和广义梯度近似(GGA)对Ca2Si的基态能带、态密度和介电函数进行计算,得到正交相是一种稳定相. 在实验方面,基于电阻率测量实验报道Ca2Si的带隙为1.90 eV. Takagi N等[7,8]应用蒸发加热处理两步法首次制备了单相的Ca2Si晶体. 杨吟野等[9-13]利用磁控溅射(MS-Magnetron-sputtering)技术,在Si(100)衬底上沉积Ca膜,然后在真空退火中获得单一相直接迁移型的Ca-Si膜.Ca-Si膜在实际生长过程中受到温度、压强、电激等影响导致晶格发生应变,影响Ca-Si膜的电学性质和光学性质,到目前为此应变对材料性能的影响的理论研究鲜见报道[14-17],但应变对Ca2P0.25Si0.75电子结构及光学性质的影响研究尚未见报道.Ca2P0.25Si0.75作为新型的半导体材料,有必要深入研究应变对其电子结构及光学性质的影响,揭示应变对其光学性质的影响机制. 因此,本文采用基于密度泛函理论的第一性原理平面波方法对应变作用下Ca2P0.25Si0.75的电子结构及光学性质进行全面的模拟计算和分析.
2 计算方法
立方晶系Ca2Si空间群为Fm3m,晶格常数为a=0.7148 nm,每个原胞有12个原子,其中8个Ca原子,4个Si原子[1].在外压稳定下Ca2Si的晶格常数a=0.4702 nm,在外压稳定下采用一个P原子置换一个Si原子形成掺杂的立方相Ca2P0.25Si0.75模型,由于立方相Ca2Si模型的4个Si原子处于等效位置,P原子的置换位置对体系的影响较小,计算采用的立方相Ca2P0.25Si0.75模型暂不考虑不同位置置换对体系的影响.
本文采用基于第一性原理的贋势平面波方法对晶格(110)应变的模拟计算,即将立方相Ca2P0.25Si0.75晶体的晶格常数a 在其晶胞优化后所得的晶格平衡值的92%~108%范围内以2%比率进行线性变化,文中所有的计算由CASTEP(Cambridge serial total energy package)软件包完成. 首先将Ca2P0.25Si0.75的体系采用BFGS(Broyden, Fletcher, Goldfarb and Shannon)算法进行几何优化,得到稳定的结构体系. 在优化后得到稳定的结构体系下分别计算不同应变的能带结构、电子态密度和光学性质. 体系的价电子波函数用平面波基矢展开并设平面波的截断能为330 eV,迭代收敛精度为5×10-6eV,选取广义梯度近似处理交换关联能部分,交换关联势计算采用PBE(Perdew Burker Ernzerhof)提出的广义梯度近似方法(GGA),采用超软贋势(Ulter Soft Pseudo Potential)计算离子实与电子之间的相互作用,计算总能量在倒易空间中进行,布里渊区积分采用Monkhorst-Pack方法K点取4×6×3.
3 结果与讨论
3.1 能带结构
由图1(d)可知,处于平衡状态的Ca2P0.25Si0.75是直接带隙半导体,带隙宽带Eg=0.51549 eV.根据Si4-态(3sσ,3sσ*,3pσ,3pπ,3pπ*,3pσ*)和晶体场分裂的Ca2+3d态(eg和t2g)对费米面附近的能带结构图作如下描述:插在费米面的三条能带为Ca2+3d-eg态,导带的第4条带线到第9条带线为P5-、Si4-的反键态3pπ*,3pσ*而第10~12条带线为P5-、Si4-的成键态3pσ,3pπ;在价带的1~2条带线为Ca2+3dt2g态(带线从价带顶向低能方向数),第3~8条带线为P5-、Si4-的成键态3pσ,3pπ.当Ca2P0.25Si0.75材料受到(110)面应力应变时,晶格常数应变使得其能带结构发生变化,由于晶格常数的变化导致导带底能量的改变,导带底附近的能谷分裂为2组简并能谷,形成导带边和次带边;价带顶能量的变化使得轻、重空穴带分离为2组能峰,形成价带变和次带变.应变的禁带宽带Eg则由上移的重空穴带顶和下移的简并能谷决定.图1(a)~(c)为施加压应变Ca2P0.25Si0.75的能带图,施加压应变后Ca2+3d态受到影响最显著,Ca2+3d-eg态向低能方向偏移,Ca2+3dt2g态向高能方向偏移.禁带宽带Eg呈现递减变化趋势,当应变达到92%时Ca2P0.25Si0.75呈现金属特性.图1(e)~(i)为施加张应变Ca2P0.25Si0.75的能带图,当施加张应变达102%时,Ca2P0.25Si0.75呈现最大直接带隙Eg=0.54378 eV,此后随着张应变的增加Ca2P0.25Si0.75带隙减小;当应变达106%时Ca2P0.25Si0.75变为间接带隙半导体,且带隙值随着应变的增加而减小.计算结果表明无论施加张应变还是压应变禁带宽带均在减小,与王冠宇[15]的结果很好的吻合.
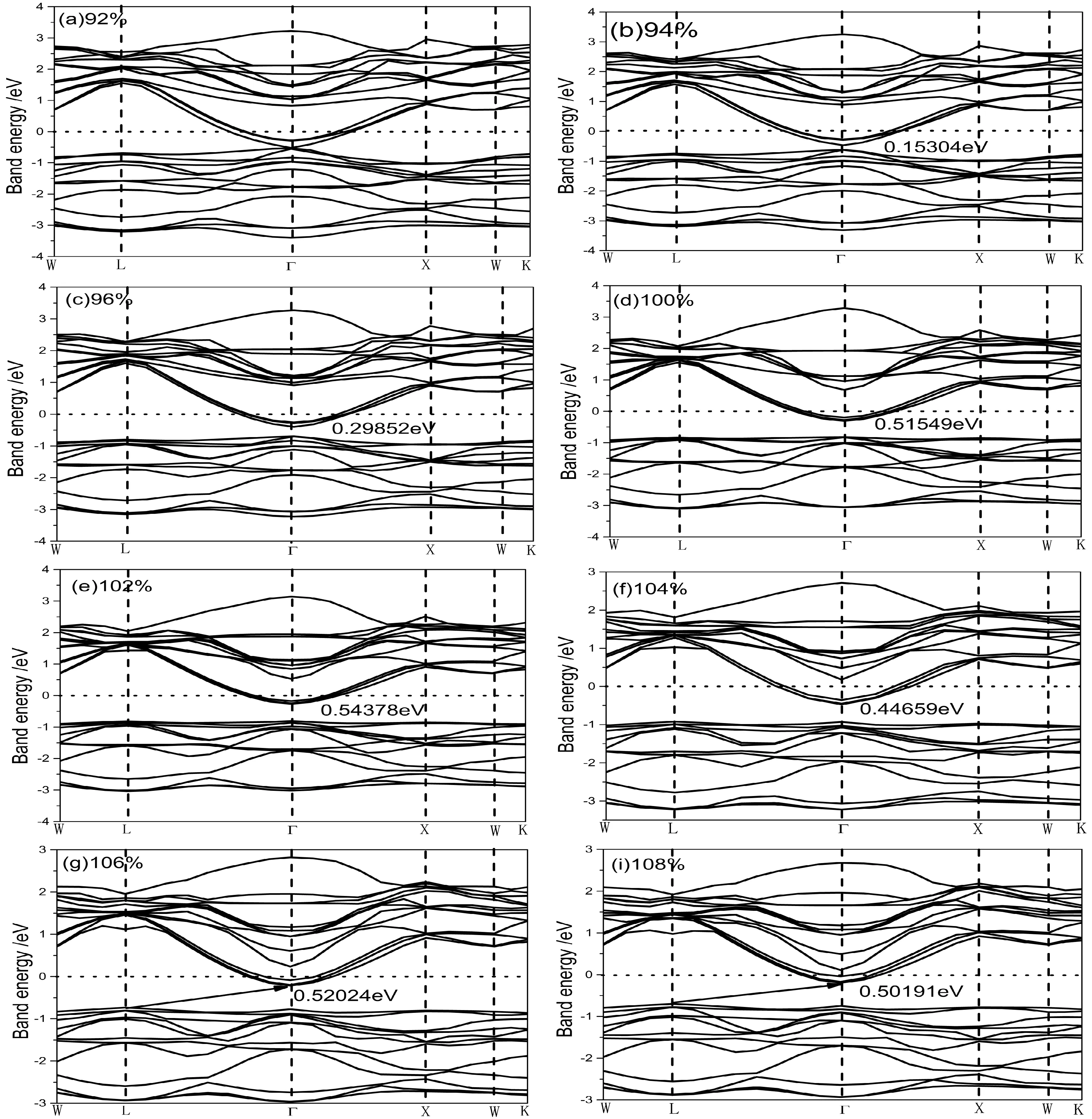
图1 应变为92%(a)、94%(b)、96%(c)、100%(d)、102%(e)、104%(f)、106%(g)、108%(h)立方相Ca2P0.25Si0.75能带结构图Fig. 1 The band structure of cubic Ca2P0.25Si0.75 in the strains of 92%(a), 94%(b), 96%(c), 100%(d), 102%(e), 104(f), 106%(g) and 108%(h)
3.2 光学性质
3.2.1 介电函数
介电函数作为沟通带间跃迁微观物理过程与固体电子结构的桥梁,通过介电函数可以得到其他各种光谱信息,Ca2P0.25Si0.75作为半导体材料,其光谱是由能级间电子跃迁所产生.图2为压应变和拉应变Ca2P0.25Si0.75的介电函数图,从图2(a)可知,平衡状态下Ca2P0.25Si0.75的静态介电常数为4.5899.张应变使得Ca2P0.25Si0.75的静态介电常数随着应变的增加而发生相应的变化,张应变为102%、104%、106%、108%对应的静态介电常数分别为8.1115、7.9285、9.0474、9.1279.当施加96%、94%的压应变时,Ca2P0.25Si0.75的静态介电常数为7.4618、7.5797.随着压应变的增加介电常数随之增加,但当Ca2P0.25Si0.75仍是直接带隙时随着张应变的增加介电常数减小;当Ca2P0.25Si0.75变为间接带隙后随着张应变的增加介电常数增加.其原因是在外力作用下导致晶体场发生变化,晶体中原子核周围的电子云发生畸变使得正负离子中心发生相对位移极化,施加单轴外力作用促使晶体中的电子畸变变得有序电极化增强.比较在相同应变条件下比较拉伸应变和压缩应变得到压缩应变对Ca2P0.25Si0.75静态介电常数的影响显著于张应变.介电函数虚部的峰值是由于电子跃迁产生,反应了Ca2P0.25Si0.75的能带结构及其他光谱信息,与未施加应变相比明显发现施加应变后介电函数虚部的峰值点增加,说明施加应变电子跃迁增强,与计算得到的能带结构变化一致,应变(压应变、张应变)使得导带向低能方向偏移,价带向高能方向偏移.
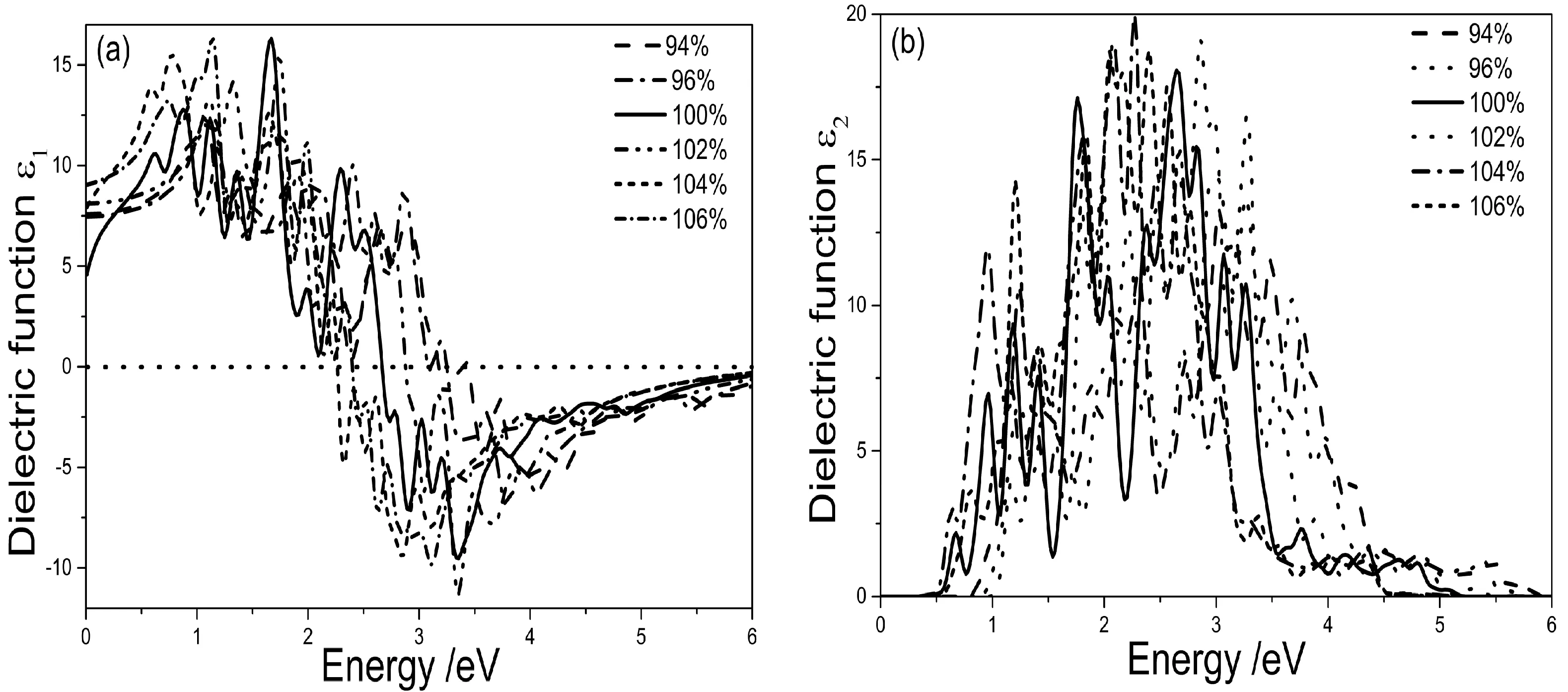
图2 应变为92%、94%、96%、100%、102%、104%、106% 立方相Ca2P0.25Si0.75的介电函数实部(a)和虚部(b)Fig. 2 The real part of dielectric function (a) and the imaginary part of dielectric function (b) of cubic Ca2P0.25Si0.75 in the strains of 92%, 94%, 96%, 100%, 102%, 104% and 106%
3.2.2 折射率
由复折射率和介电函数的关系ε1=n2-k2,ε2=2nk得到Ca2P0.25Si0.75的复折射率,图3为Ca2P0.25Si0.75的折射率和消光系数.由图3(a)可知,平衡状态下Ca2P0.25Si0.75的折射率为2.1424.拉应变使得Ca2P0.25Si0.75的折射率随着应变的增加而呈现与带隙值相同的变化规律,拉应变为102%、104%、106%、108%对应的折射率分别为2.8480、2.9177、2.9712、3.0213;当施加压应变时,Ca2P0.25Si0.75的折射率随着压应变的增大折射率呈准线性增加,压应变为96%、94%对应的折射率分别为2.7316、2.7531.当光子能量在约5.5 eV~6.5 eV的能量范围,折射率趋于零,这与下文的反射谱在该能量范围的反射率趋于1相对应,表明(110)面拉伸作用下Ca2P0.25Si0.75在这些能量范围呈现出金属反射特性.计算所得折射率n的值与静态介电常数完全对应.由图3(b)可知,其变化曲线在0.7 eV附近漂移,当施加压应变时消光系数k的峰值和数目与未施加应变比较是逐渐减少,表明在这个能量范围施加压应变其光学响应减少,同时消光系数在带边表现出强烈的吸收特征.而施加张应变时消光系数k的峰值和数目逐渐增加,表明在这个能量范围施加压应变其光学响应增加.其原因是应变使得Ca2P0.25Si0.75晶体中原子核周围的电子云发生畸变,能带结构和费米面附近的电子态密度分布发生变化所致,对电子跃迁产生影响.
3.2.3 反射谱
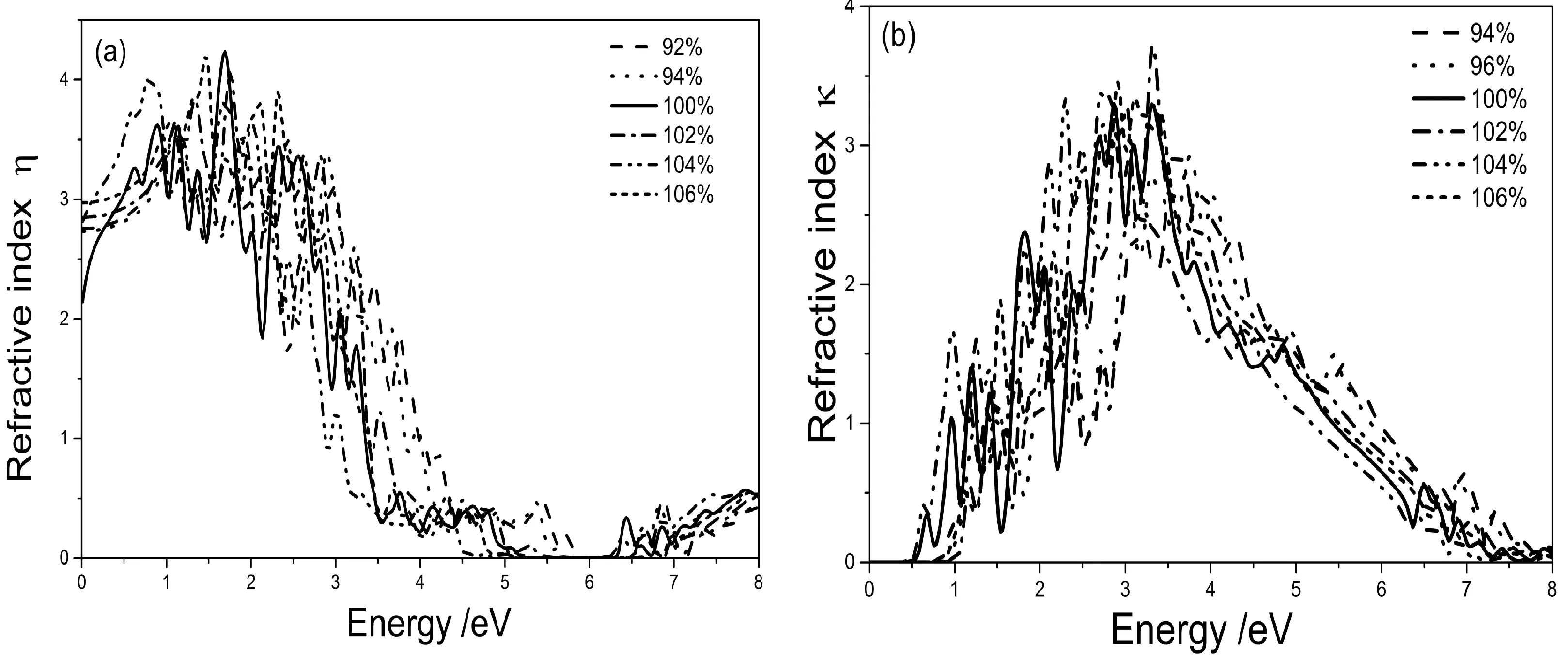
图3 应变为92%、94%、96%、100%、102%、104%、106% 立方相Ca2P0.25Si0.75的复折射率(a)和消光系数(b)Fig. 3 The refractive index (a) and the extinction coefficient (b) of cubic Ca2P0.25Si0.75 in the strains of 92%, 94%, 96%, 100%, 102%, 104% and 106%
反射区域,张应变(拉伸晶格)会增大Ca2P0.25Si0.75发生反射区域,反射谱与文中计算的折射率和吸收系数完全对应.
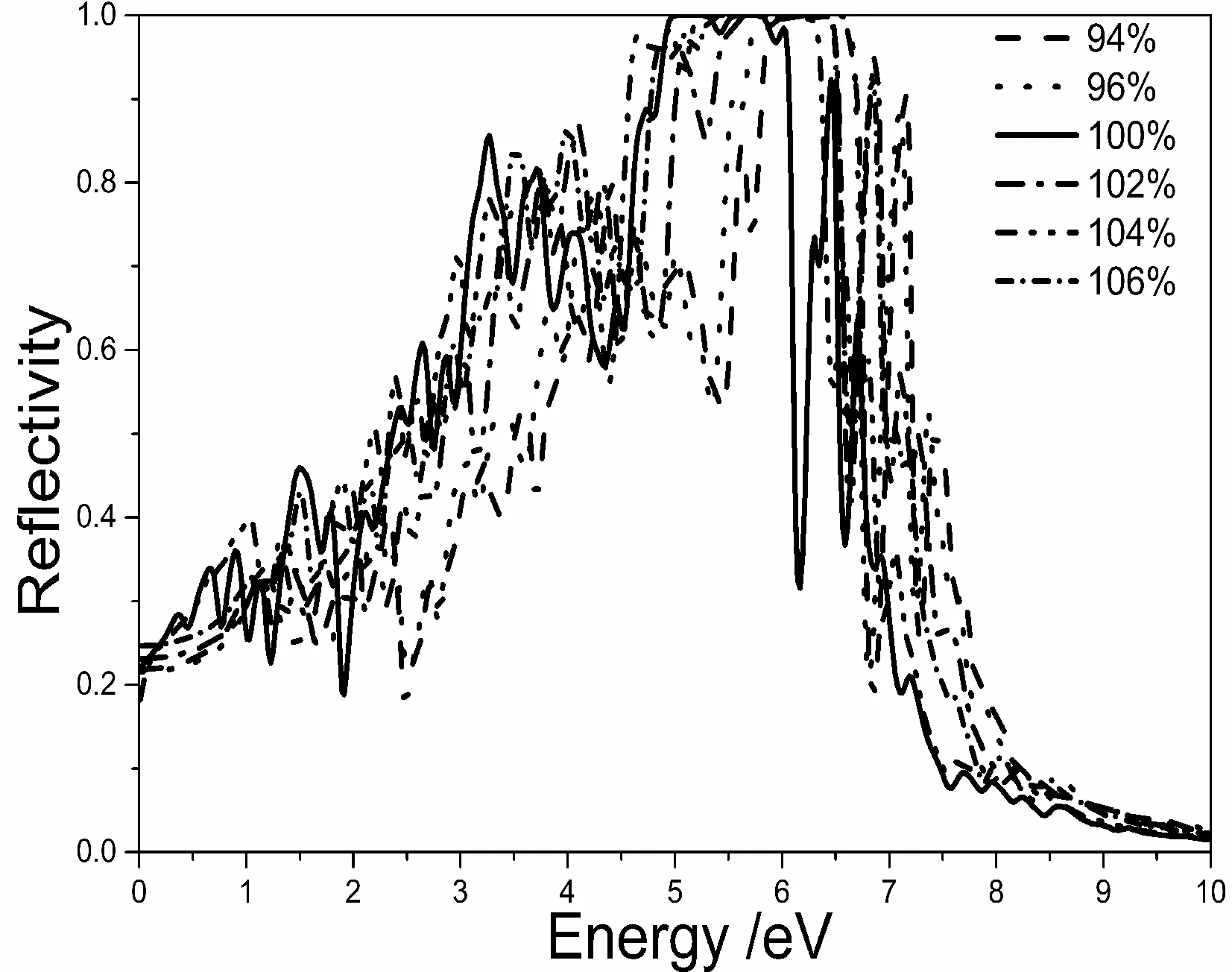
图4 应变为92%、94%、96%、100%、102%、104%、106% 立方相Ca2P0.25Si0.75的反射谱Fig. 4 The reflectivity of cubic Ca2P0.25Si0.75 in the strains of 92%, 94%, 96%, 100%, 102%, 104% and 106%
3.2.4 吸收谱
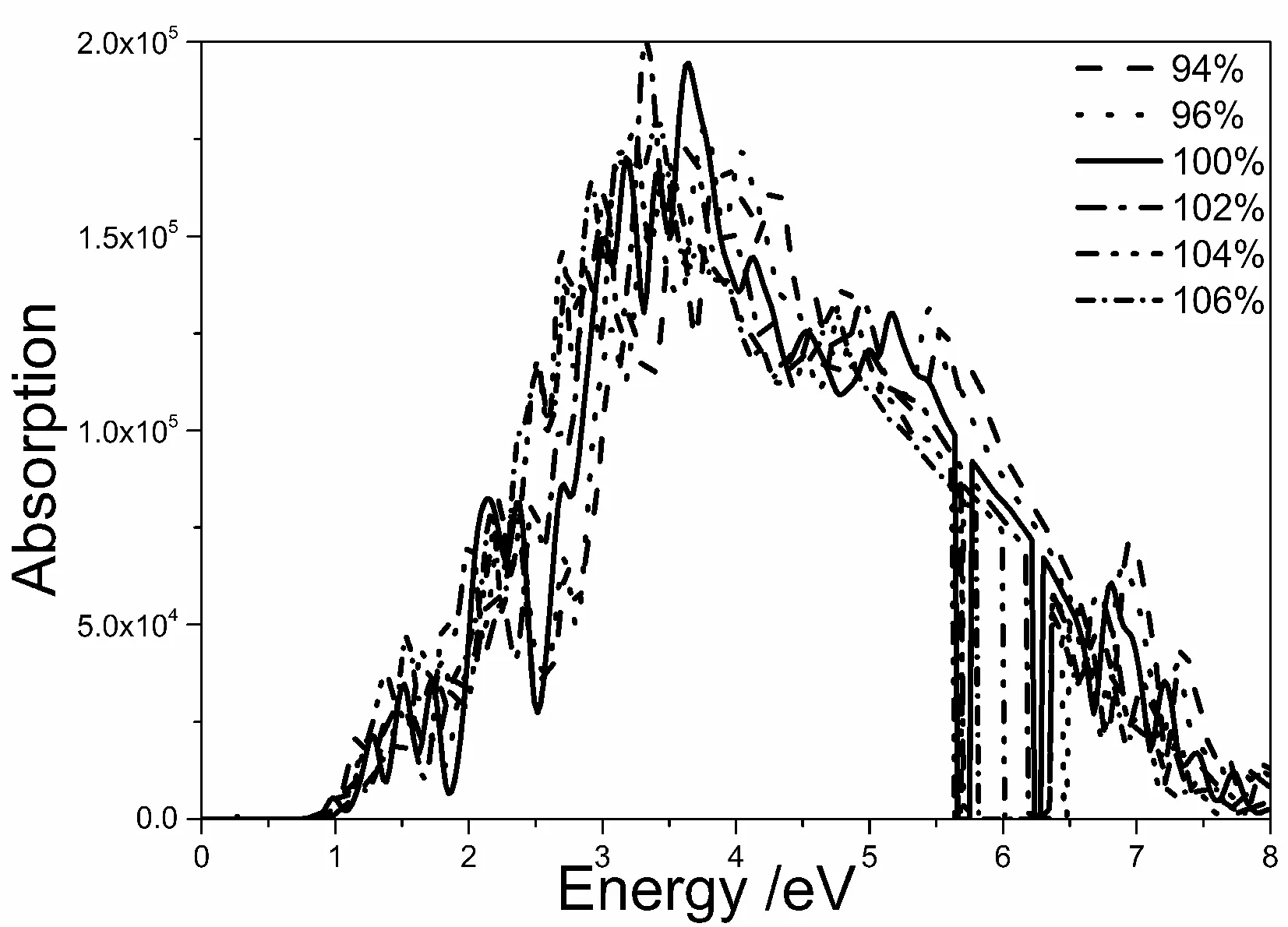
图5 应变为92%、94%、96%、100%、102%、104%、106% 立方相Ca2P0.25Si0.75的吸收谱Fig. 5 The absorption of cubic Ca2P0.25Si0.75 in the strains of 92%, 94%, 96%, 100%, 102%, 104% and 106%
4 结 论
采用基于密度泛函理论的第一性原理平面波超软贋势方法,模拟研究了应变作用下Ca2P0.25Si0.75(110)面发生晶格形变时的能带结构、介电函数、复折射率、吸收谱、反射谱等光学性质.计算得到:Ca2P0.25Si0.75(110)面在晶格发生100%~92%压应变时,Ca2P0.25Si0.75仍然直接带隙半导体,但带隙随着应变增加而减小;Ca2P0.25Si0.75(110)面在晶格发生100%~102%张应变时,Ca2P0.25Si0.75禁带随着张应变的增加而增加;当张应变在102%~104% Ca2P0.25Si0.75禁带随着应变的增加而减小,晶格应变大于104%后Ca2P0.25Si0.75转变为间接带隙且禁带宽带随着张应变的增加而减小.随着压应变的增加介电常数随之增加,但当Ca2P0.25Si0.75仍是直接带隙时随着张应变的增加介电常数减小;当Ca2P0.25Si0.75变为间接带隙后随着张应变的增加介电常数增加.施加应变均能够使得Ca2P0.25Si0.75的折射率增加,施加压应变折射率随着应变的增加而减小;施加张应变折射率随着应变的增加而增大.施加压应变吸收系数增加,反射率减小;施加张应变吸收系数减小,反射率增加.综上所述,应变可以改变Ca2P0.25Si0.75的电子结构和光学常数,是调节Ca2P0.25Si0.75光电传输性能的有效手段
[1] Lebègue S, Arnaud B, Alouani M. Calculated quasiparticle and optical properties of orthorhombic and Ca2Si [J].Phys.Rev. B, 2005, 72(8): 1.
[2] Imai Y, Watanabe A. Energetics of alkaline-earth metal silicides calculated using a first-principle pseudo potential method [J].Intermetallics, 2002, 10(4): 333.
[3] Matsui H, Kuramoto M, Ono T,etal. Growth of Ca2Si layers on Mg2Si/ Si(111) substrates [J].Cryst.Growth, 2002, 237-239: 2121.
[4] Cheng J, Yang Y Y, Liang Y. Selective growth of Ca2Si film in Ca-Si system by R.F MS by annealing [J]. 3M-NANO, 2012, 9: 75.
[5] Imai Y, Watanabe A, Mukaida M. Electronic structures of semiconducting alkaline-earth metal silicides [J].JournalofAlloysandCompounds, 2003, 358 (1-2): 257.
[6] Migas D B, Miglio L, Shaposhnikov V L,etal. Comparative study of structural, electronic and optical properties of Ca2Si, Ca2Ge, Ca2Sn and Ca2Pb [J].Phys.Rev. B, 2003, 67(20): 205203.
[7] Takagi N, Sato Y, Matsuyama Tetal. Growth and structural properties of Mg2Si and Ca2Si bulk crystals [J].AppliedSurfaceScience, 2005, 244 (1-4): 330.
[8] Busch C, Junod P, Katz U,etal. Electrical conductivity of the intermetallic compounds Ca2Si, Ca2Sn, Ca2Pb, ZnSb [J].Helv.Physical.Acta, 1954, 27: 193.
[9] Yang Y Y, Xie Q. The selective growth of a single phase calcium silicide film in the Ca-Si system by R.F. [J].MagnetronSputtering, 2008, 4688419: 360.
[10] Yang Y Y, Xie Q. Growth characteristics of calcium silicides film from the deposited Ca films at the different sputtering Ar pressure[C].Shanghai:ChinaISCSCT, 2008, 1: 484.
[11] Yang Y Y, Xie Q. A single phase semiconducting Ca-silicide film growth by sputtering conditions, annealing temperature and annealing time [J].JournalofMaterialsScience, 2009, 44(14): 3877.
[12] Yang Y Y, Xie Q. The selective growth of a single phase calcium silicide film in the Ca-Si system by R.F. magnetron sputtering [J].ASID, 2008, 8: 360.
[13] Yang Y Y, Xie Q. The selective growth of a single phase Ca-silicide film from Ca-Si system by R.F. magnetron sputtering and by annealing [J].InternationalJournalofInformationandElectronics, 2008, VI, N2-4(33): 6.
[14] Wang G Y, Ma J L, Zhang H M,etal. Model of intrinsic carrier concentration of [110]/(001)-uniaxial strained Si [J].ActaPhys.Sin., 2011, 60(07): 077105(in Chinese) [王冠宇, 马建立, 张鹤鸣, 等. [110]/(0001)单轴应变Si本征载流子浓度模型[J]. 物理学报, 2011, 60(07): 077105]
[15] Cui D M, Jia R, Xie Q,etal. First-priciples calculations of stressed Ru2Si3[J].ChinesejouralofLuminescence, 2011, 32(09): 907(in Chinese) [崔冬萌, 贾锐, 谢泉, 等. Ru2Si3在应力作用下的第一性原理研究[J]. 发光学报, 2011, 32(09): 907]
[16] Hu Z X, Wu Y X, Gu S L,etal. Varying characteristics of crystal structures and optical properties of ZnO under pressure [J].ChineseJournalofquantumelectronics, 2010, 27(05): 613(in Chinese) [胡智向, 吴玉喜, 顾书林, 等. 外压调制下ZnO晶体结构与光学性质变化特性的研究[J]. 量子电子学报, 2010, 27(05): 613]
[17] Yan W J, Zhang C H, Gui F,etal. Electronic structure and optical properties of stressed β-FeSi2[J].ActaOpticaSinca, 2013, 33(07): 0716001(in Chinese) [闫万珺, 张春红, 桂放, 等. 应力作用下β-FeSi2的电子结构及光学性质[J]. 光学学报, 2013, 33(07): 0716001]
The effect of strain at the (110) surface on the energy band structure and optical properties of cubic Ca2P0.25Si0.75
CEN Wei-Fu, YANG Yin-Ye, FAN Meng-Hui, YAO Juan, YANG Wen-Bang, HUANG Jin-Bao
(College of Science, Guizhou Minzu University, Guiyang 550025, China)
Energy band structure and optical properties of the cubic Ca2P0.25Si0.75strained on the (110) surface have been calculated by the first-principle pseudo-potential method based on density functional theory (DFT). The results show that in the strain range 92%~100%, Ca2P0.25Si0.75is direct band gap semiconductor where the band gap decreases with the increase of strain, the conduction band moves to low-energy, while the valence band moves to high-energy. In the strain range 100%~102% band gap increases with the increasing strained, and in the strained of 102%, the direct band gap is maximum Eg=0.5437 eV. In the strain range 102%~104% the band gap decreases with the increase of strained, and in the strain of 104% Ca2P0.25Si0.75turn to indirect band gap semiconductor where the band gap decreases with the increasing of strain. The dielectric constant and refractive index of cubic Ca2P0.25Si0.75are increased by strained, the absorption increases and the reflectivity decreases by compressive strained, but the absorption decreases and the reflectivity increases by the tensile strained. In conclusion, the strain can transform the energy band structure and optical properties of the cubic of Ca2P0.25Si0.75, so, it is an effective method of adjusting the photoelectric transmission performance of cubic Ca2P0.25Si0.75.
Strained; Optical properties; Energy band structure; First-principles; Ca2P0.25Si0.75
2014-02-21
国家自然科学基金(51266002);教育部科学技术研究重点项目(210200);贵州省科学技术联合基金项目(LKM201130);贵州省优秀科技教育人才省长专项资金项目(201174)
岑伟富(1988—), 男,布依族,硕士研究生,主要从事电子功能方面研究.E-mail:cenweifu1988@sina.cn
杨吟野.E-mail:Ythin1969@sohu.com
103969/j.issn.1000-0364.2015.12.021
0472.+3
A
1000-0364(2015)06-1038-06

