光腔耦合阵列中四模方形Cluster态的制备
魏素娟, 周 坚, 孙利辉, 田永红
(量子光学与信息光子学研究中心, 长江大学物理与光电工程学院, 荆州 434000)
光腔耦合阵列中四模方形Cluster态的制备
魏素娟, 周 坚, 孙利辉, 田永红
(量子光学与信息光子学研究中心, 长江大学物理与光电工程学院, 荆州 434000)
提出一种四模方形cluster态的制备方案, 方案选用四个分别包含一个原子系综的独立单模光腔, 光腔之间用短光纤实现耦合.讨论证明在合适外加激光脉冲的驱动下, 可确定性的制备得到稳定的四模方形cluster态.通过调节驱动激光的频率和相位, 该方案可以拓展到多模和其他形cluster态的制备.
cluster态; 原子系综; 连续变量; 量子纠缠
1 引 言
自2006年张靖和Braunstein等人提出连续变量cluster态的概念[1], 有关cluster态的研究就吸引了人们广泛的研究兴趣.因其具备比Greenberger-Home-Zeilinger(GHZ)态的纠缠更难以破坏, 可以克服离散变量模型中可能出现的问题等优点[2,3], 基于连续变量纠缠态的量子信息的研究得到迅速发展[4-8].Cluster态已被证实有诸多应用.例如, 在线性光学方案中, cluster态可用来确定性的设计可控X操作[9]; 可利用cluster态和纠缠光模实现连续变量单向量子计算[10];2006年Menicucci等人还提出可以运用压缩光源、线性光学辅助和连续变量cluster态, 实现量子计算的构想[3]; 2009年张靖等人还特别提出连续变量四模方形cluster态可作为实现量子网络的重要资源[11].因此, 连续变量cluster态的制备对于连续变量量子信息的发展具有重要意义.
迄今为止有大量的制备方案被提出, 这些方案大致可分为两类.一类是基于线性光学方案: 2012年苏晓龙等人利用压缩光和线性光学转换实现了连续变量多粒子cluster态的实验制备[12], Menicucci等人利用单模真空器设计了制备cluster态的实验[13], 最近苏晓龙等人又提出了通过局部傅里叶变换和相位旋转制备cluster态的方案[14], Pfister等人提出量子光频梳制备cluster态的方案[15], Pooser等人也提出了类似的方法[16].
这些线性光学方案都需要压缩光作为初始光源, 需要在分离玻色模之间产生纠缠.因此, 这些方案要解决许多实际问题如: 要实现压缩光和分束器间的强耦合、要具备高度压缩的压缩光, 而解决这些问题的难度会随着目标态模式数的增加而增加.随着原子系综概念的提出, 因其是大量全同原子的集合, 如果大量原子的集合叠加态能实现和光场的耦合, 原子系综就能和光场有效耦合[17].另外由于原子基态寿命较长, 退相干现象明显减弱, 可以实现量子态的长寿命高保真存储.基于此, 出现了很多利用原子系综制备cluster的方案[18,19].柯莎莎等人提出了在环形腔中利用原子系综制备连续变量cluster态的方案[20], 在此基础启发下, 我们改环形腔为光腔耦合阵列, 光腔之间用短光纤实现耦合, 利用原子系综与腔模之间的耗散相互作用, 施加合适频率和相位的激光驱动, 实现四模方形cluster态的单步确定性制备.
2 模型和主方程
2.1 理论模型
如图1所示, 制备四模方形cluster态的模型选用四个独立的光腔, 在每个光腔中放置一个原子系综, 假设每个原子系综包含N个全同四能级原子.在相互作用绘景中, 系统的哈密顿量为:
H=Hcc+Hac+Hal
(1)
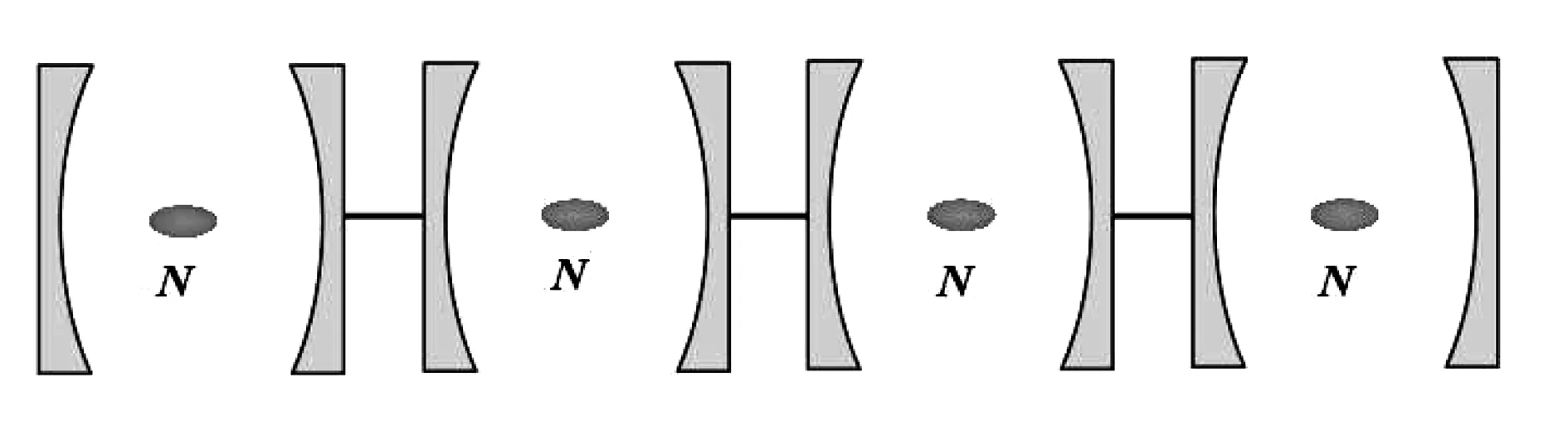
图1 制备四模方形cluster态的模型Fig. 1 A model for preparation of four-mode square cluster states
这里Hcc为耦合腔模之间的相互作用哈密顿量:
H.c.]
(2)
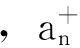
Hac为原子与腔场之间的相互作用哈密顿量:
|sjn〉〈1jn|)e-iΔt+H.c.]
(3)
如图2所示为腔场中四能级原子的能级图, |0jn〉和|1jn〉 表示第n个原子系综中两个稳定的基态, |μjn〉和|sjn〉表示两个激发态.跃迁|0jn〉→|μjn〉 和|1jn〉 →|sjn〉 之间的耦合强度分别为gμn和gsn(gμn=gsn=g), 腔模频率ωc与跃迁频率ω0μ和ω1s的失谐分别用Δμn和 Δsn表示,并假设Δμn=Δsn=Δ.
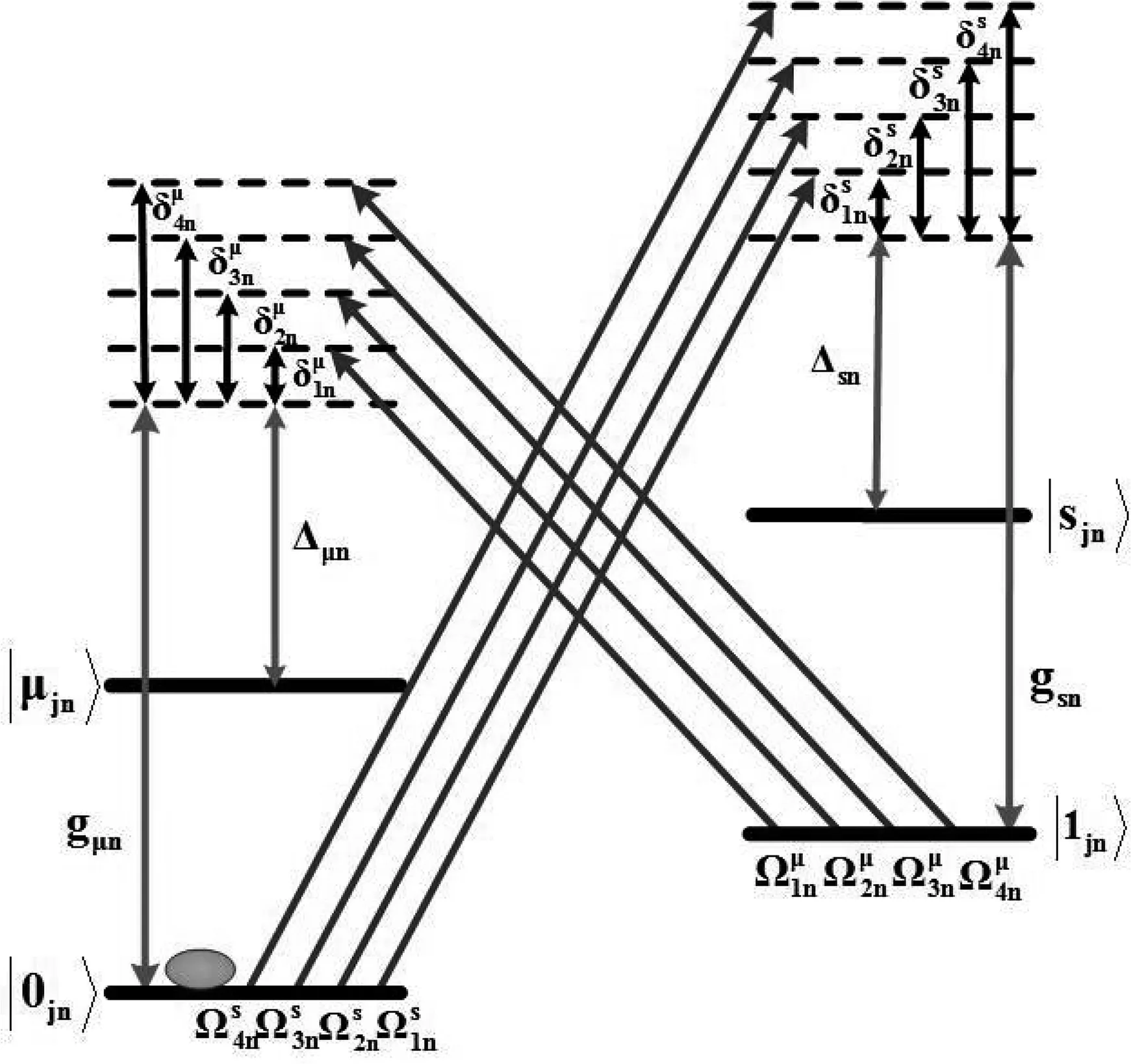
图2 原子能级结构图和原子跃迁与激光场耦合结构图Fig. 2 Atomic level configuration and the coupling configuration of the laser to the atomic transitions
Hal为原子与驱动光场之间的相互作用哈密顿量:
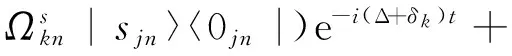
(4)
2.2 主方程
首先我们把Hcc对角化,要引入玻色算符:
(5)
(6)
根据对角变换中算符an和cn的关系,Hcc取其对角形式:
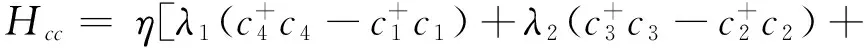
(7)
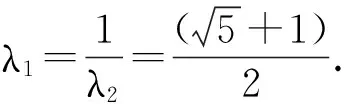
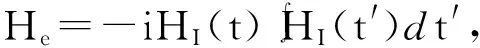
(8)
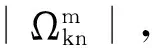
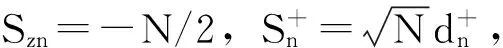
exp(iHe1t)Heexp(-iHe1t)-He1
(9)
为了补偿Stark位移,我们引入了He1:
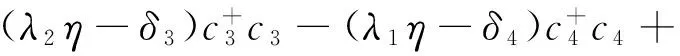
(10)
这样就得到最终的原子与场相互作用哈密顿量:
(11)
其中:
(12)
这里我们舍弃常数能量项并选择:
(13)
从方程(11)可以看出由于耗散相互作用集合模与腔模之间产生了非线性压缩型耦合.
在这种情况下, 系统主方程:
(14)
可以约化为:
(15)
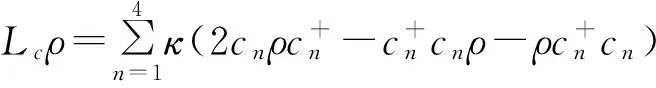
3 四模方形cluster态的制备
3.1 方形cluster态
下面讨论根据前面得到的有效哈密顿量(11)制备四模方形cluster态:
4d1d3-4d2d4)-H.c.]|0d〉
(16)
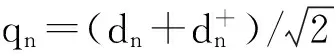
(17)
(18)
显然当ξ→∞时, 方差趋于零.因此, 根据cluster态的定义[21],态|ψs〉是类方形四模cluster态.
3.2 频率和相位的调节
下面讨论如何实现四模方形cluster态的制备.首先由图1给出的理论模型可做如下的么正变换dLn=TdnT+:
(19)
显然, 模dLn是相互正交的, 态|ψL〉可以写为:
(20)
这样, 每个dLn模都可以制备到目标态.
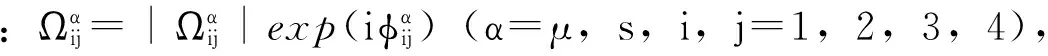
(21)
相位应取为:
(22)
有效哈密顿量变为:
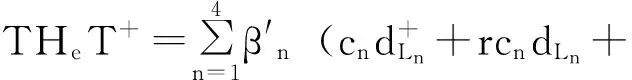
(23)

3.3 目标态的制备
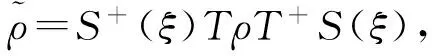
(24)
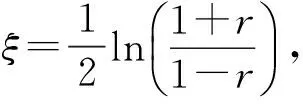
=|ψS〉〈ψS|⊗|0cn〉〈0cn|
(25)
即系统处于纯态, 这里|ψS〉=T+S(ξ)|0dLn〉是纯方形连续变量cluster态.
4 结 论
本文提出利用光腔耦合阵列制备四模方形cluster纠缠态的方案.针对本文提出的理论模型, 只需要正确调节激光的拉比频率与相位, 就可以实现四模方形cluster态的确定性单步制备.这种方法对光腔品质因素要求不高, 不需要精确控制序列激光脉冲的宽度, 可为实现大规模的量子网络提供理论参考.
[1]ZhangJ,BraunsteinSL.Continuous-variableGaussiananalogofclusterstates[J].Phys.Rev.A, 2006, 73:032318.
[2]RaussendorfR,BriegelHL.Aone-wayquantumcomputer[J].Phys.Rev.Lett., 2001, 86: 5188.
[3]MenicucciNC,LoockP,GuM, et al.Universalquantumcomputationwithcontinuous-variableclusterstates[J].Phys.Rev.Lett., 2006, 97: 110501.
[4]BraunsteinSL,LoockP.Quantuminformationwithcontinuousvariables[J].Rev.Mod.Phys., 2005, 77:513.
[5]LauH,WeedbrookC.Quantumsecretsharingwithcontinuous-variableclusterstates[J].Phys.Rev.A, 2013, 88: 042313.
[6]MenicucciNC.Fault-Tolerantmeasurement-basedquantumcomputingwithcontinuous-variableclusterstates[J].Phys.Rev.Lett., 2014, 112: 120504.
[7]CaiXH,QiaoNS,PengGH.Entanglementconcentrationoftheentangledsqueezedstatebytwo-levelatominteractingwithcavityfields[J].J.At.Mol.Phys. (原子与分子物理学报), 2011, 28: 117 (inChinese)
[8]ZhangL,QiangWC.SchemeforpreparationofWstateincavityQED[J].J.At.Mol.Phys.(原子与分子), 2015, 32(2): 229 (inChinese)
[9]WangY,SuX,ShenH, et al.Towarddemonstratingcontrolled-Xoperationbasedoncontinuous-variablefour-partiteclusterstatesandquantumteleporters[J]. Phys. Rev.A, 2010, 81: 022311.
[10]UkaiR,IwataN,ShimokawaY, et al.Demonstrationofunconditionalone-wayquantumcomputationsforcontinuousvariables[J].Phys.Rev.Lett., 2011, 106:240504.
[11]ZhangJ,AdessoG,XieC, et al.QuantumteamworkforunconditionalmultipartycommunicationwithGaussianstates[J].Phys.Rev.Lett., 2009, 103: 070501.
[12]SuX,TanA,JiaX, et al.ExperimentalpreparationofquadripartiteclusterandGreenberger-Horne-Zeilingerentangledstatesforcontinuousvariables[J]. Phys.Rev.Lett., 2007, 98: 070502.
[13]MenicucciNC,MaX,RalphTC.Arbitrarilylargecontinuous-variableclusterstatesfromasinglequantumnondemolitiongate[J].Phys.Rev.Lett., 2010, 104: 250503.
[14]SuX,ZhaoY,HaoS, et al.Experimentalpreparationofeight-partiteclusterstateforphotonicqumodes[J]. Opt.Lett., 2012, 37: 5178.
[15]MedeirosdeAraujoR,RoslundJ,CaiY, et al.Fullcharacterizationofahighlymultimodeentangledstateembeddedinanopticalfrequencycombusingpulseshaping[J]. Phys. Rev.A, 2014, 89: 053828.
[16]PooserR,JingJ.Continuous-variablecluster-stategenerationovertheopticalspatialmodecomb[J]. Phys. Rev.A, 2014, 90: 043841.
[17]DuanLM,CiracJI,ZollerP.Three-dimensionaltheoryforinteractionbetweenatomicensemblesandfree-spacelight[J]. Phys. Rev.A, 2002, 66: 023818.
[18]HammererK,SrensenAS,PolzikES.Quantuminterfacebetweenlightandatomicensembles[J]. Rev. Mod. Phys., 2010, 82: 1041.
[19]ZhengSB,YangZB,XiaY.Generationoftwo-modesqueezedstatesfortwoseparatedatomicensemblesviacoupledcavities[J]. Phys. Rev.A, 2010, 81: 015804.
[20]LiGX,KeSS,FicekZ.Generationofpurecontinuous-variableentangledclusterstatesoffourseparateatomicensemblesinaringcavity[J]. Phys. Rev.A, 2009, 79: 033827.
[21]YukawaM,UkaiR,LoockP, et al.Experimentalgenerationoffour-modecontinuous-variableclusterstates[J]. Phys. Rev.A, 2008, 78: 012301.
Preparation of four-mode square cluster states in the optical coupled cavity array
WEI Su-Juan, ZHOU Jian, SUN Li-Hui, TIAN Yong-Hong
(Institute of Quantum Optics and Information Photonics, School of Physics and Optoelectronic Engineering, Yangtze University, Jingzhou 434000, China)
We propose a scheme for preparation of four-mode square cluster states.We consider a chain of four single-mode cavities coupled with short fiber, each contains an atomic ensemble.We will show that a four-mode square cluster state can be deterministically prepared by driving the atomic ensembles with suitable laser pulse.The procedure can be extended to the case of multimode and other shape cluster states by choosing right frequencies and phases.
Cluster states; Atomic ensemble; Continuous variable; Quantum entanglement
103969/j.issn.1000-0364.2015.12.020
2015-04-26
国家自然科学基金青年基金(11304024); 长江大学基础学科科学研究发展基金支持计划项目(2013cjp12)
魏素娟(1989—), 女, 湖北咸宁人, 硕士研究生, 主要从事量子光学方向的研究. E-mail: 1126356585@qq.com
孙利辉. E-mail: lhsun@yangtze.edu.cn
0431.2
A
1000-0364(2015)06-1033-05

