“学讲计划”课例探究——记一类不等式问题的“整合”与“创新”

缪苇伟（江苏省徐州市丰县中学）

高中阶段，不等式的恒成立问题是一种重要题型，学生普遍感觉较难.一方面是题目的类型和形式多样；另一方面是方法灵活多样、思维含量较高．涉及函数的图像与性质、导数及其应用，渗透着换元、化归、数形结合等思想方法．不等式恒成立问题多与参数的取值范围问题联系在一起，往往与函数的单调性、极值、最值等相关．对于不等式恒成立的常用解题方法已是老生常谈的问题，本文在这里就不再阐述．但我们知道不等式恒成立问题形式千变万化，考题亦常考常新，而对于一些题目，学生即使采用常规的方法去解决，仍然会出现不少的新问题．在此类现象的基础上，作者结合近期我校实行的“学讲计划”这一新课改模式，对复习试卷上出现的不等式问题，及时进行了此类问题的讲评.在课堂上除了对此类问题的常规解题方法进行“整合”以外，在其他方面也进行了“创新”，把一节试卷讲评课变成了一节探究课，让学生在“学讲计划”课改模式下不断领悟和总结，从而促使学生在解决此类问题的能力上得到改善和提高.

一、课堂实录（摘录）

教师：我们继续讲评试卷，请看第18题

教师：上述解法是我们这次练习中出现的一类解法，并且比较集中，现在请各小组认真分析上述解法的正确与否，然后请几位同学把交流讨论的结果进行阐述.

学生分组活动：3分钟后

甲组代表：老师，本题解法好像无误，我也是这样做的，仍不明白错误何在.

乙组代表：不正确是肯定的了，但是我有点不明白这里面的m的作用；

教师提示：刚才甲组同学说得很好，这里m的作用是什么？还有，本题是解关于谁的不等式？

丙组代表：好，我明白了，不正确，这里m的作用是参数，本题是解关于x的不等式，应该用m来表示不等式的解集；

教师：很好，这位同学总结的好，本题中的m与x并不是双自变量，是解关于x的不等式，m的作用是参数，但此解法误认为是不等式恒成立问题，这也是此解法错误的根源，正确解法应该是用m来表示不等式的解集.请同学们继续思考，应该如何给出正确解法呢？

【教师整合一】

提高对不等式恒成立问题的本质认识

在解决此问题的过程中，由于学生对不等式恒成立问题的本质模糊不清，把解不等式与不等式恒成立混为一谈，导致了上述的错解，所以在教学过程中，教师要提高学生对不等式恒成立问题的本质认识．可见，学习数学不仅仅是使用数学公式、数学方法解题，更重要的是对基本数学概念、数学方法、数学模型的深刻理解，从而丰富学生的科学知识，培养学生的分析能力和科学的探究能力，全面地培养学生的科学素养．课堂教学如何培养学生的科学素养，应作为教学设计的重要指导思想之一．

在此基础上，继续设置针对性的练习，让学生巩固.

教师：既然同学们认识了不等式恒成立问题的本质，下面请思考导学案上例1的变题解法的正确性.

变题：已知函数 f（x）= λx+sinx是区间［－1，1］上的减函数，若 f（x）=t2+ λt+1在 x∈［－1，1］恒成立，求的取值范围．

投影错误解法：因为 f（x）= λx+sinx是区间［－1，1］上的减函数，所以f′（x）=λ+cosx≤0在区间［－1，1］上恒成立．

所以 λ ≤ -1，且［f（x）］max=f（－1）＝ －λ － sin1．

不等式 f（x）≤ t2+ λt+1 对于 x∈［－1，1］恒成立，

所以只需-λ-sin1≤t2+λt+1成立，即不等式（t+1）λ+t2＋1＋sin1≥0对λ≤－1恒成立．

令 m（λ）=（t+1）λ +t2+1+sin1．

学生分组活动：3分钟后

丁组代表：根据不等式恒成立计算出不等式-λ-sin1≤t2+λt+1是正确的，但在解决不等式-λ-sin1≤t2+λt+1（λ≤-1）时出现了同上题一样的错误，此处情景的描述不是不等式恒成立问题，本题在此处的本质是解关于t的不等式，其中参数λ满足λ≤-1．

教师总结：这位同学回答得非常好，现在看起来对不等式问题的认识已经掌握，这个解法比较由于比较复杂，现在我把过程投影给同学们参考，课后请同学们自行完善.

正解：因 f（x）= λx+sinx在［-1，1］上是减函数，

所以f′（x）=λ+cosx≤0，在区间［-1，1］上恒成立．

所以 λ ≤ -1，且［f（x）］max=f（-1）=-λ -sin1．

所以只需-λ-sin1≤t2+λt+1，其中λ≤-1．

教师：既然同学们认识了不等式恒成立问题与解含参数的不等式的区别，那么我们下面继续来研究如何解决不等式恒成立问题，请看导学案例2（2）.

例2 （2）已知，f（x）=x4-4x3+（3+m）x2-12x+12，m∈R，若对于任意实数x，f（x）≥0恒成立，求m的取值范围．

戊组代表：此题可用导数求解，简洁明了.

当 x=2 时，g（2）=7．

所以 g（x）得最大值为 g（2）=7，

所以m+3≥7，即m≥4．

综上可知：的取值范围是［4，+∞）．

【教师整合二】

转化为最值问题是解决不等式恒成立的常用方法

不等式恒成立问题通用解法是通过化归的方式把转化成函数的最值问题．函数最值的求解是函数学习中的一个难点，而用导数求解，则流程明确、可操作性强、易于把握，是求最值的常用方法之一．

按理说，到这里已经把试卷中的一类典型错误评讲清晰，完成了，但就恰恰此时，一位学生的发言改变了课堂的预先设计——

学生甲：老师，我们组讨论的结果是此法太麻烦，有更简便的方法：

容易判断当x=2时，函数y=m（x），y=n（x）同时取得最大值．

又因为 m（2）=4，n（2）=3，

所以当 x=2 时 g（x）=m（x）+n（x）有最大值 7．

所以m+3≥7，即m≥4．

综上可知：m的取值范围是［4，+∞）.

学生齐鼓掌——学生已经完全沉浸在喜悦之中，享受着“学讲计划”课堂、享受着数学带来的乐趣——学生的思路已经盘活，立竿见影，马上又出现了新的解法：

学生乙：我们组的方法比他们组更简便，解法如下：

f（x）=x4-4x3+（3+m）x2-12x+12=（x2+3）（x-2）2+（m-4）x2，

当 m<4 时，f（2）=4（m-4）<0 不成立，

当 m ≥ 4 时，f（x）=（x2+3）（x-2）2+（m-4）x2≥ 0 对一切x∈R恒成立．

所以m的取值范围是［4，+∞）.

此时，课堂已经沸腾了——

我及时根据学生的发言，进行了“二度教学设计”，及时整理思路，调整教学方案，让学生结合近期的模拟题以及去年的高考题，把不等式恒成立问题的研究方法进行汇总，适度进行了创新，效果甚好.

栽植方式有穴植法和沟植法2种。栽植的深度应与移植前保持一致或者稍微浅一些，对于出叶的花卉不能栽植过深，以免出现烂根情况，移植过后不能浇水过多，应等到新根长出后再进行浇水。还应确保植株的通风效果。在遮阴条件或者天气较为干燥时，通过植株喷雾或者喷水的方式促进生根。新移植的花卉重新栽植后，会出现一段时间的萎蔫，停止生长，这种情况是一种正常现象，待新的根系长出以后，将会重新生长。折断时期称为缓苗期。通常为保证花卉的长势，以及园林景观的早日形成，缓苗期越短越好。具体在挖苗时可以通过多带土的方式有效避免伤根，降低对花卉根系的影响，从而有效缩短缓苗期。

二、不等式恒成立问题的“四大攻略”

攻略一：求导是基本，而不是惟一

课堂上，针对学生的解法，我适时进行了表扬，并对解法进行了总结：求导是基本方法，但并不是惟一方法.求导方法思路清晰，学生易于接受．但是求导、因式分解等计算会让很多学生望而却步．所以在解决这类问题时提醒学生：在利用导数解决这类问题较繁琐时，不妨换换思路，让学生感受不同的方法在此处的应用．

攻略二：以形辅数，数形结合

我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事非”．“数”与“形”反映了事物两个方面的属性.通过“以形辅数、数形结合”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的．

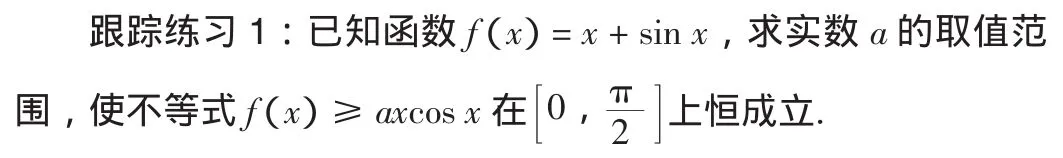
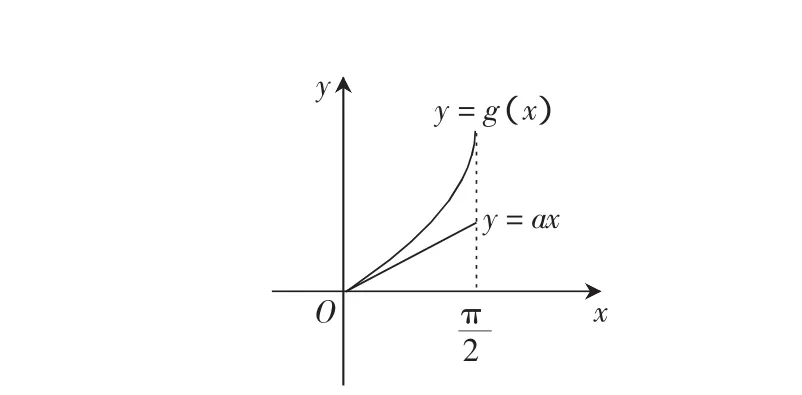
则a≤g′（0）=2．

由（1）（2）可知 a≤ 2．

因此，训练学生要看他们能否将已学过的知识与该问题相迁移，能否找到恰当而熟悉的函数模型表述题意，能否把数学过程分析明白，并结合题意转化为形象而直观的图像，进而使化难为易，这都是值得教师重视的．

攻略三：会当凌绝顶，一览众山小

整体意识是一种全面地、总体地考虑问题的思维习惯或自觉意识，它注重问题的整体结构和结构的改造，能从整体上把握思维方向和进程．解题中应用整体意识考虑问题，能增加思维的有效性，达到另辟蹊径的效果，有助于培养思维的灵活性和创造性．仍然以跟踪训练1为例，如果学生具有这种整体意识的话，做如下处理就很顺理成章．

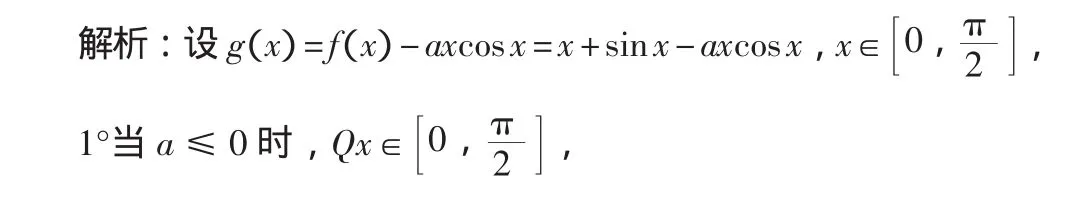
综上所述，实数的取值范围为a≤2．

此解法中三次使用整体意识，一处在当a≤0时，直接判断g（x）≥0恒成立；第二处在02时又改变了函数的结构，通过构造新的函数来解决问题.事实上，在解决不等式恒成立问题的过程中，构造新函数也是常见的解决方法．三处整体意识的使用，直接把题目的思维量降了下来．

攻略四：大处着眼，小处着手

局部意识是能通过细节来把握整体情况．所以要想顺利解决问题，不仅要熟练掌握基础知识和灵活运用解题方法，更重要的是掌握一定的技巧，才能达到快速求解的目的，有些数学问题，如果从整体上不便解决，可先研究其局部．

跟踪练习2：（2011浙江文科 21） 设函数 f（x）=a2lnxx2+ax，a>0.

（1）求 f（x）的单调区间；

（2）求所有的实数 a，使 e-1 ≤ f（x）≤ e2对 x∈［1，e］恒成立．

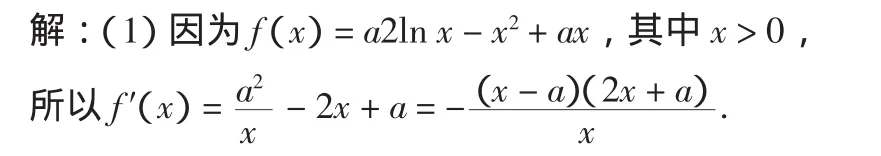
由于 a>0，所以f（x）的增区间为（0，a），减区间为（a，＋∞）．

（2）由题意得，f（1）＝a－1≥ e－1，即a≥ e．

由（1）知 f（x）在［1，e］内单调递增，要使 e－ 1 ≤ f（x）≤e2，对 x∈［1，e］恒成立，

函数 f（x）满足 e－ 1 ≤ f（x）≤ e2对 x∈［1，e］恒成立，则对于区间［1，e］上的局部值也是满足的．在此题中选择了f（1）这个局部值，通过f（1）这个局部值可以得到参数a的大致范围，为后续的问题处理带来方便．此数学意识中要求学生有较强的观察能力，根据函数、不等式和区间的特点来选择合适的局部值．所以在解决数学问题时，要善于找到事物之间的内在联系，回归到较为浅显的知识，就能有一种“柳暗花明又一村”的感觉．

罗增儒教授也曾经说过：新课改所倡导的教学理念经过十年的贯彻，必然会与数学学科有机结合，产生出既区别于其他学科，又区别于传统数学教学新特色．“学讲计划”的实施也不例外．因此，在“学讲计划”实施过程中，我们要防止一种倾向掩盖另一种倾向．遗憾的是，探究合作泛滥，传统的具有启发性的“讲授法”缺位；以学生为主体的思想泛滥，教师的主导作用缺失；表演作秀，重形式轻实质；无效讨论、合作的形式化；满堂发问，师生对话过于频繁；探索泛化，放任自流等现象在现阶段数学教学中较为突出.

“学讲计划”对教师提出了更高的要求．教学过程中需要教师能正确处理好“教”与“学”的双边和谐关系，具有诱导学生使其“想学”、指导学生让其“会学”、辅导学生令其“能学”的技能．实现“学讲计划”是一个长期而又复杂的工程，需要坚持不懈地探索与追求．“学讲计划”要以教师教的转变促进学生学的转变．

［1］罗增儒.评课的视角，课例的切磋［J］.中学数学教学参考，2014（1-2）：14.