挖掘课本习题 构建高效课堂

李家宇（安徽省合肥市长丰县第一中学）

《数学课程标准》指出：学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探索、动手实践、合作交流等学习数学的方式.这些方式有助于发挥学生学习的主动性，使学生的学习过程成为在教师引导下的“再创造”过程.同时，高中数学课程设立“数学探究”学习活动，为学生形成积极主动的、多样的学习方式进一步创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯.

那么怎样将自主探索、动手实践、合作交流等学习方式落到实处，构建起高效愉悦的课堂是每个老师都迫切需要解决的课题，我认为深度挖掘课本例题习题，创新问题情境是解决上述问题的一个好办法.

课本中每一个例题的设置都有其目的和作用，体现着本节知识应达到的能力要求.我们不仅要紧扣课本，认识到认真钻研课本的重要性，突出课本基础知识的作用，突出课本例题中数学思想方法的挖掘和应用，也要重视课本习题潜在功能的挖掘与利用.指导学生回归课本，依“纲”固“本”，挖掘课本潜在功能，对课本典型问题进行引申、推广、探究，为学生形成积极主动的、多样的学习方式进一步创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯.这不仅是《数学课程标准》要求的，也与高考命题的“源于课本，高于课本”的理念是相吻合的.

在使用《普通高中新课程标准实验教科书人教A版选修2-1》时我进行了一些尝试，感觉取得了很好的效果.

案例一：课本P41面的例2

例2 如图，在圆x2+y2=4上任取一点P，过点P作轴x的垂线段PD，D为垂足．当点P在圆上运动时，线段PD的中点M的轨迹是什么？

分析：点P在圆x2+y2=4上运动，由点P移动引起点M的运动，则称点M是点P的伴随点，因点M为线段PD的中点，则点M的坐标可由点P来表示，从而能求点M的轨迹方程．

解法剖析：①（代入法求伴随轨迹） 设 M（x，y），P（x1，y1）；

②（点与伴随点的关系）因为M为线段DP的中点，

【点评】本例所用到的方法是“代入法求伴随轨迹”.课本的用意是让同学们理解并学会用这样一种方法求一类点的轨迹.如果教师只是就例讲例，而不对课本进行深入的挖掘，那就太可惜了.学生也会认为只是个普通的例题而已，而失去了学习的主动性，学生的学习过程成为在教师引导下的“再创造”过程也将荡然无存了.

我在和同学们探讨完上面的例题后，紧接着给出了课本P50面B组第一题：

教师：这里的圆是确定的，不同的是改变了M的位置，大家可否先猜想一下M的轨迹呢？

学生：应该还是椭圆吧？

教师：为什么呢？

学生：因为和例2很相似，点P移动引起点的运动，点M是还点P的伴随点，只不过关系式改变了，实际还是受点P的控制.

教师：可否用相同的方法求解呢？

教师：回答得相当不错，请同学们试着做一下.（待大家得出正确的结论后，几何画板展示拖动，是椭圆）

教师：纵观这两道题，可有更一般化的题设和结论吗？

学生：老师，我想可以把圆x2+y2=4换成更一般的圆x2+y2=R2，按照刚才的求法，例2和习题1应该是焦点分别在x轴和y轴上的椭圆.

变式教学是中国传统数学的瑰宝.通过以上的探讨，使同学们把握住轨迹问题中有一类是“变化中又有不变性”的问题，并掌握了解决方法.在这个过程中，同学们深刻体会到提出猜想，严格证明，体验感悟，思想共鸣等一系列探究活动开展是很好的，因为他们更容易弄清问题的实质.

类似的做法我还应用到了对《人教A版选修2-1》P41面的例3上.

在学过双曲线后，我又和同学们一起探讨了k值为正数时，动点C的轨迹方程.（为双曲线）.

在课堂教学过程中，教师对课本例题习题进行深度的挖掘，改变题目的条件或结论，通过自主探究，培养学生手脑结合，注重实践的习惯.不仅可以让学生主动参与知识的形成过程，了解知识的来龙去脉，还能促进学生思维的发展，有助于激发学生创新意识，提高学习活动效率.

高中数学课程应该首先强调对数学本质的认识，否则会将生动活泼的数学思维活动淹没在形式化的海洋里.因此数学课应该返璞归真，努力揭示数学概念、法则、结论的发展过程和本质.解析几何的轨迹问题由于具有较强的综合性且具有动态的因素，题目多变，解题方式灵活，同学们对此很不容易把握.很多老师对解析几何的教学感到头疼.其实利用“几何画板”辅助一下教学，让同学们直观感受解析几何中轨迹问题的实质，不失为一种有效的办法.我在上完“双曲线”后对这种方法进行了尝试.

案例2：《人教A版选修2-1》P49面第7题

如图，圆O的半径为定长r，A是圆O内一个定点，P是圆上任意一点.线段AP的垂直平分线l和半径OP相交于点Q，当P点在圆上运动时，点Q的轨迹是什么？为什么？

教师：猜猜看，点Q的轨迹是什么呢？

学生：可能是椭圆吧？

教师：“可能”一词用得相当好，因为还没有证明.还只是猜想.我们来看一看（几何画板动态演示），确实是椭圆，能否证明呢？

学生：这里OP是定长r，连接QA，则由l是线段AP的垂直平分线可知 OA =QP即 OA +QO =QP +QO =r是一个定长，焦点是O和A，长轴是r.

教师：很好.想想AP的中点D的轨迹是什么呢？

学生：还是椭圆么？

教师：我们应该从什么角度去思考啊？几何关系.大家看，点还是受控制的吧.我们来看一看.（几何画板演示，轨迹是一个圆），怎样解释呢？

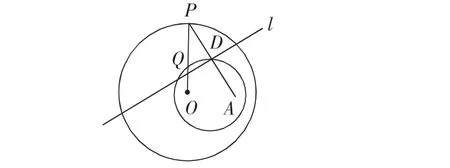
教师：再看，把A点放在圆外，线段AP改为直线AP，其他条件不变，点Q的轨迹会是什么情形呢？我们来看一看，大家来找几何关系.

学生：双曲线.（学生感叹轨迹的奇特，数学真好玩，一点也不枯燥）.

反思：教师首先对课本进行深挖掘利用好课本的例题习题，选择合适的探究素材，预设和课题具有实质联系的数学实验活动和数学问题作为对象.借助“几何画板”直观地体现数学的本质，并且让学生感到好玩.

高效的数学课堂是一种追求，更是一种境界.需要我们不断日积月累，需要我们用自身创造、精心设计，我们教师要潜心研读教材，充分挖掘教材中的本质，使数学教学与培养学生健康心理有机结合，努力为学生创建学习的乐园，达到教书育人的目的.