民办高职院校《高等数学》教学现状及改革的设想

周巧娟

（应天职业技术学院，江苏 南京210046）

高等数学作为高等职业院校工科类学生必修的一门重要的基础课程，对学生后继课程的学习和思维素质的培养起着重要的作用。然而，在实际的教学过程中，高等数学的教学效果并不理想，主要体现在以下几个方面：

（1）学生基础薄弱，接受能力较差[1]

近年，随着高等教育事业的普及与发展，高等职业教育的入口变低，特别对于民办高职院校而言，注册招生使得学生入学变得更为简单，但带来的很大问题就是相当一部分学生的数学基础非常薄弱，有的甚至是零。这部分学生接受高数知识的能力非常有限，同时他们的学习方法、学习习惯也存在着不少问题，这就使得高等数学对于他们而言犹如天书。

（2）缺乏学习动力，厌学情绪高涨

民办高职院校生源素质总体不高，不少学生学习成绩一直是比较靠后，因而，他们缺乏学习的积极性和信心，总认为自己不是学数学的料，肯定学不会。所以，不学就不懂，不懂就更不学，从而进一步加重了厌学的情绪。

（3）内容多，课时少，应用能力欠缺

现有的教学模式注重高等数学的系统性和完整性，力求学生通过教师的讲解能建立起比较清晰的逻辑框架，把概念定理吃透。这种授课模式不仅需要大量的课时去讲解概念、定理和解题方法，也忽略了学生用数学知识解决实际问题的能力。而近年，各高职院校普遍加强了专业课程建设，减少了公共基础课的教学课时，这也加剧了高数课程内容多，课时少的矛盾。

为了改善高数的教学效果，使高数更好得发挥其重要作用，我们必须从原有的教学模式中挣脱出来，有所突破和创新，加快《高等数学》教学改革的步伐。下面就针对以上提出的问题谈谈我对《高等数学》教学改革的一些设想。

1 主要的改革方向及改革措施

高职院校《高等数学》教学应以“以应用为目的，以必需、够用为度”的原则设置教学内容，因此《高等数学》改革的方向是要满足专业需求，关注学生应用能力的培养，兼顾到不同层次学生的发展需求[2]。因此，高职院校的《高等数学》改革应从模块化教学开始[3]。

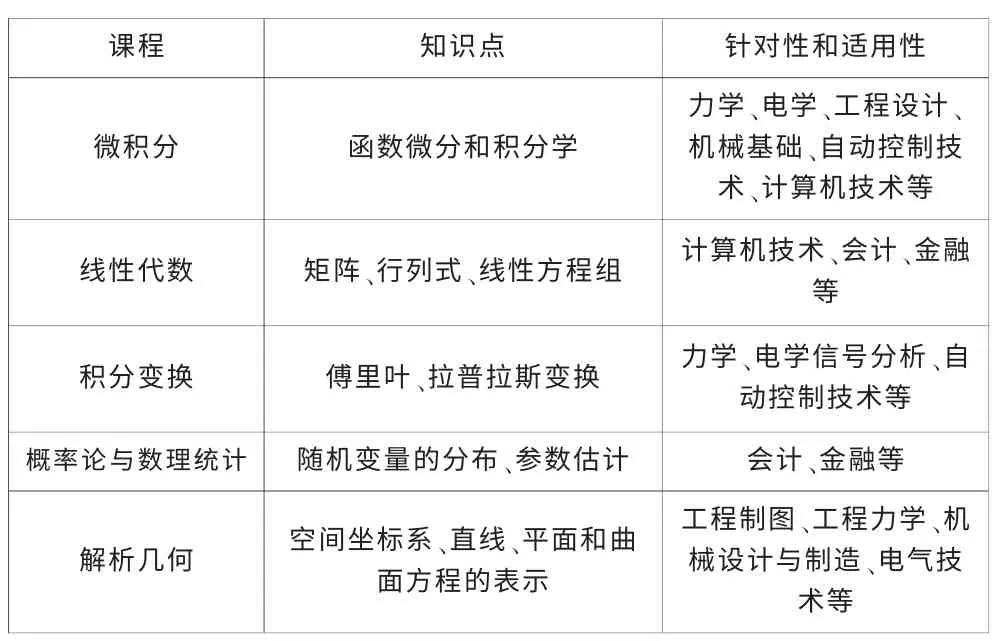
表1 高等数学的知识点与专业课程的关系分析

1.1 模块的划分

高职院校的数学教学一般只涉及到《微积分》、《线性代数》和《概率论与数理统计》，为了更好的为专业服务，通过对我校相关专业的调研，我们将高等数学的知识点与专业课程的关系分析如表1：

通过以上分析，我们将数学分为以下四个模块：衔接模块（必修），主要介绍初等数学的相关知识，通过该模块的学习，使学生比较容易得从初等数学过渡到高等数学，解决基础较弱的学生的知识衔接问题；基础模块（必修），主要介绍一元微积分，这部分内容，是各专业所需的共性的知识；专业模块（必选），主要包括以下七个内容：线性代数、常微分方程、空间解析几何、多元微积分、积分变换、级数、概率统计初步，各专业选择相关的内容学习；提高模块（任选），主要针对需继续深造的同学。

1.2 各专业需求模块

模块划分好后可由各专业教师根据专业需要选择教学模块，比如下表列出了我校一些专业所需模块内容：

表2 专业需求模块表

在教学实践中根据专业需要可对模块的设置和选择进行调整，逐步完善模块化的教学内容体系。

1.3 其他方面的改革措施

1.3.1 教学手段的改革

目前，我们大多数老师采用的均是传统的黑板+粉笔的教学手段。此种教学手段有一定的弊端，课堂容量小，学生视觉容易疲劳。我们将进一步尝试使用多媒体辅助教学，多方刺激学生的感官，节省课堂有限的时间。另外，我们应该逐渐将Matlab等数学软件引进高等数学的教学中，将教学的重点放在数学思想的学习、数学思维的培养和数学方法的应用上，将复杂的计算交给数学软件去完成，这样既能增强学生学习的积极性，又能培养学生用数学解决实际问题的能力。

1.3.2 教学方法的改革

在授课的过程中，结合学生特点，采用多种方法相结合的方式促进学生对概念和方法的理解和掌握。比如，抽象的概念形象化。以案例引入概念，以问题驱动，淡化论证。比如在讲极限时，教材从抽象的形式极限概念讲起，大多数学生感到难以掌握，所以在介绍极限的数学语言定义之前，可以列举具有中国传统文化表述极限思想的极限例子：“一尺之棰，日取其半，万世不竭”；李白在《黄鹤楼送孟浩然之广陵》中的名句“孤帆远影碧空尽，唯见长江天际流”，当我们在理解无穷小量是以零为极限的变量时，如果在脑海中能出现一幅“一叶孤舟随江流远去，帆影在逐渐缩小，最终消失在水天一际之中”这样的图景，数学概念也就融合在这美的诗意中了。除此之外，还可以多用数形结合法、口诀法、案例法等等，让学生学起来比较容易，也比较有意思。

1.3.3 教材的改革

现有的高职教材普遍强调高等数学的系统性和完整性，难度较大。对民办高职院校的学生来说，本身难度就不能大，因此我们需要一本真正适合民办高职院校的教材，而我们现在编写的教材遵循“难度适合、突出应用”的原则。一方面，按模块化设计，在每一模块后增加了数学实验部分，简化了教学内容；另一方面，围绕具体案例展开知识点，增加了数学文化和数学应用部分，提升学生的学习兴趣，注重培养学生应用数学知识解决实际问题的能力。

1.3.4 考核方式的改革

改变现有的一张试卷定成绩的模式，大量增加过程性的考核，不同的模块由不同的考核方式，重点考核学生用数学的能力。

2 主要的改革目标

模块化教学模式为学生提供了多层次、多种类的选择，通过改革，我们希望能够达到以下几点目标：

（1）符合民办高职院校学生的认知规律：在讲授的内容和难度上有所取舍，淡化基础，强调应用，在有趣的课堂教学过程中对数学思想和数学方法有一定的掌握。

（2）更好得为专业服务：通过模块化教学避免了所有专业都学一样的内容，“按需来学”既提高了教学的实用性，也解决了课时不够的问题。

（3）转变学生对数学教学的传统看法：选择教学模块学习突出了“以应用为目的，以必需、够用为度”的原则，让学生能够感到“学有所用”，能够做到“学以致用”。

（4）培养学生数学思维，数学素质：在每个模块讲解过程中加入相关知识点的起源、发展过程和应用实例，培养学生学数学和用数学的能力。

总的来说，我们要通过教学的改革将高数课程建设为既能满足专业学习和专业发展需要，又能为培养学生数学思维，数学素质发挥功能性作用。在教学理念、教学模式、教学方法、课业评价等方面不断创新的课程，使高等数学能更好发挥其重要作用。

［1］刘自团，杨旭辉.浅析民办高职院校教学中存在的问题及对策[J].高等职业教育：天津职业大学学报，2008,17(1)：19-21.

［2］吴建祥，王瑜.浅谈高职院校高等数学教学模式改革的探索[J].中国科教创新导刊，2011(14)：18.

［3］黄金超.高职院校高等数学模块化教学研究：以滁州职业技术学院机电系为例[J].滁州职业技术学院学报，2011,10(1)：20-23.