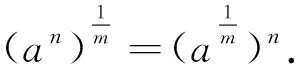关于指数函数、对数函数与幂函数的教学探索
韩茂安
(上海师范大学数学研究所,上海200234)
1 引 言
指数函数ax(其中a>0,a≠1,a∈)、对数函数logax(其中a>0,a≠1,x>0)与幂函数xα(其中α∈,x>0)是数学分析中三类基本的初等函数, 它们在所述的定义域上都是严格单调的, 连续的, 并且满足下列熟悉的性质:
ax+y=ax·ay,axy=axy,
(1)
logaxy=logax+logay, logaxα=αlogax,
(2)
(3)
这些性质在中学数学的教材中出现过, 但没有给出证明,甚至当x与y均为有理数时也没有证明(1)式.
笔者查阅了一批数学分析教材, 只发现式(1)在文[1]中作为定理出现(见[1]中第四章定理4.10), 但文[1]只证明了式(1)的第一式(我们发现式 (1)第二式的证明将用到[1]中第四章定理4.11, 这可能是[1]的作者未曾想到的), 文[2] (第一卷第一分册)对式(1)的第一式也有证明, 但对第二式只提及x与y为有理数的情形. 式 (2)的第二式在文[1]中也出现过 (见[1]中第一章第4节式(2)), 其推导要用到式(1)的第二式, 而式 (2)的第一式以及式(3)在文[1,2]等许多数学分析教材中均没有证明.
本文有如下两个目的:
①用两种不同的思路证明式(1), 我们发现其证明将用到指数函数的连续性与有理幂函数的连续性, 这表明文[1]中第四章的定理4.10与4.11需要做一些调整;
②利用式(1)给出(2)与(3)等公式的严格证明.
以上两点可以弥补数学分析教材的内容缺失,建立数学分析教材与教学在基本初等函数的性质方面的系统性和完整性, 也是笔者最近几年主讲数学分析的一点教学心得.
2 指数函数与对数函数的定义与性质
首先, 我们回顾中学数学对指数函数ax(其中a>0,a≠1)的定义:

按照上面定义, 对任何有理数r,ar都有意义, 而且不难证明ar作为r的函数关于有理数r是严格单调的,且式(1)对任何有理数x与y成立(这是中学里学过的,也是不难推出的,但为了完整,我们在本文附录中给出证明).
现设x为无理数, 按文[1], 有如下定义(见[1]中第一章第3节定义2):
文[1]利用ar关于有理数r的单调性证明了下列性质(见[1] 中第一章第4节例6):
性质1指数函数ax(其中a>0,a≠1)在其定义域上是严格单调的, 且当a>1(0 如所周知,对数函数logax定义为指数函数ax的反函数, 由于严格单调函数的反函数也是严格单调的, 故成立 性质2对数函数logax(其中a>0,a≠1)在其定义域0,+∞上是严格单调的, 且当a>1 (0 由反函数的性质, 可得下列两个等式恒成立 alogax=x,x>0, (4) 由文[1]第四章定理4.10与定理4.11知下列性质成立(我们给出两种证法) 性质3设a>0,a≠1, 则 (i)ax+y=ax·ay,x,y∈; (ii)ax在上连续. 证法一文 [1]定理4.10中利用ax的定义证明了结论(i), 而后在定理4.11中又利用结论 (i)及 证明了结论(ii). 这一思路的详细过程这里不再重复. 证法二与上述思路不同, 我们先利用性质2证明结论(ii), 而后利用结论(ii)来证明结论(i). 设x0∈,下证 ∀ε>0,不等式ax-ax0<ε等价于 ax0-ε (5) 不妨设ε logaax0-ε 或 logaax0+ε 令 则δ>0, 且当x-x0<δ时有ax-ax0<ε, 故ax在上连续. 为证结论(i), 取两个有理数列xn与yn, 使当n→∞时xn→x,yn→y, 则由结论 (ii)及归结原则知 在进一步给出指数函数的性质之前, 作为预备,先给出有理幂函数的一个性质. 性质4设r为有理数, 且r≠0, 则幂函数xr在0,+∞上是严格单调的, 并且是连续的. 性质5设a>0,a≠1, 则对任意实数x与y, 有axy=axy. 证法一这一证法需要用到指数函数定义、性质1、性质3中指数函数的连续性及性质4. 今以a>1为例证之. 又不妨设xy≠0.由axy的定义, ∀ε>0,存在有理数r≤xy,使axy-ε ar≤ar1r2=ar1r2≤axr2≤axy. 上式用到函数ax与xr2的单调性, 故有 axy-ε 由ε的任意性知axy≤axy. 下分x>0与x<0两种情况分别讨论. 若x>0, 则由axy的定义, ∀ε>0,存在有理数r≤y,使 axy-ε 由于幂函数xr与指数函数ax均连续, 故 从而 axy-ε 由ε的任意性知axy≤axy. 若x<0, 则axy作为y的函数是连续的, 故∀y∈R,∀ε>0,存在有理数r≥y, 使 故也有axy≤axy. 证法二上述证法比较繁琐, 这里再提供一个较巧妙和简单的证明, 只用到指数函数和有理幂函数的连续性. 取两个有理数列rn与sn, 使当n→∞时,rn→x,sn→y, 则由性质3(ii)和性质4知 性质6设a>0,a≠1, 则 (i) logaxy=logax+logay,x>0,y>0; (ii)logaxα=αlogax,x>0; (iv)logax在x>0上连续. 证由性质3(i)与式(4)知 alogax+logay=alogax·alogay=xy, 两边取对数即得结论(i). 由性质5与式(4)知 xα=alogaxα=aαlogax, 两边取对数即得结论(ii). 仍由性质5与式(4)知 alogablogbx=alogablogbx=blogbx=x, 两边取对数可得 logablogbx=logax. 即得结论(iii). 由性质1与性质3(ii)知对数函数作为指数函数的反函数是连续的, 即得结论(iv). 上述性质的结论(iii)就是中学里讲过但没有证明过的换底公式. 由上述性质的结论(i)与(ii)可知, 对x>0,y>0有 利用指数函数的定义, 即知下述幂函数的定义: 证由性质5知 xα=eαlnx, 故由性质1与性质2知当α>0<0时xα为严格递增(严格递减)的, 且由性质3(ii)与性质6(iii)及复合函数的连续性知xα在x>0上是连续的. 性质8对任意正实数x与y, 成立 (i)xyα=xαyα; 证由性质5、性质3(i)、性质6(i)可得 xαyα=eαlnxeαlny=eαlnx+lny=eαlnxy=xyα. 进一步由性质5和上式又得 即得结论. 于是由解的唯一性知 (A.1) 从而有 (A.2) 如果r<0, 则利用ar=(a-1)-r来定义ar. 可证, 若n为正整数, 则 (A.3) 事实上,由定义知 即得(A.3)第一式. 进一步利用该式及(A.1)可得 以及 进一步利用(A.2)与性质4可证 命题1设a>0,a≠1, 则 (i) 对任何有理数r1与r2, 成立ar1+r2=ar1·ar2,ar1r2=ar1r2; (ii) 有理幂指数函数ar关于有理数r是严格单调的. 同样,由(A.2)可知 于是(ar1)r2=ar1r2.即得结论(i). (ii) 由 (i)知(ar)-1=(a-1)r,故不妨设a>1,由(i)知,若r1与r2为两个有理数,且r1 [参 考 文 献] [1] 华东师范大学数学系. 数学分析(上册)[M]. 4版.北京:高等教育出版社,2010. [2] 菲赫金哥尔茨.微积分学教程[M].叶彦谦,等译.北京:高等教育出版社,2010.
logaax=x,x∈.
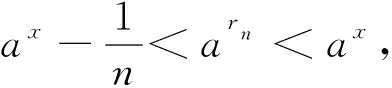

3 幂函数的定义与性质
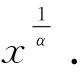
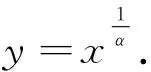
4 附录A