基于泰勒级数展开的一点超前差分公式的推导

张雨浓， 邓健豪， 刘锦荣， 仇 尧， 金 龙

(1.中山大学信息科学与技术学院，广东广州510006； 2.中山大学软件学院，广东广州510006)

1 引 言

数值微分是数值分析中的基本问题，同时也是应用科学中非常有用的一个工具[1-3]. 通过使用邻近的离散数据点，有限差分法可有效地近似一个函数在目标点的导数值[4]. 根据目标点在采样区间中的位置，有限差分公式可以被划分为前向差分、后向差分和中心差分公式. 目标点是所用数据点的最左点即为前向差分，最右点为后向差分，中间点为中心差分.

使用多点中心差分公式时，要求目标点两侧有相同数量的离散数据点. 因此，当目标点靠近边界时，单边数据点不足，多点中心差分公式往往不能被应用. 当未知函数在目标点的导数值发生加速变化时，由于前(后)向差分公式只应用单边的数据点，可能无法适应该变化，使得近似导数值的误差较大.

为了解决以上问题，一点超前差分公式被提出[5]. 该公式综合了三种传统的差分公式，在后向差分公式的形式上“前移”一点，解决了因单边数据点不足造成的问题，同时适应了目标点的导数值可能发生的加速变化[5]. 该公式由拉格朗日插值多项式推导而来. 利用采集的等间距数据点，可以构造近似未知函数的拉格朗日插值多项式；对该式子求导，即可得到近似的未知函数的一阶数值差分公式[6]，由此可以得出求一阶导数的一点超前公式.

不同于文献[5]和[6]中利用拉格朗日插值多项式来推导一阶数值差分公式的方法，本文提出了基于泰勒级数展开[7]的对一点超前差分公式的推导. 由给出的未知函数在指定区间上的N+1个等间距点的函数值，即可列出N个关于目标点的1到N阶导数的泰勒级数展开式. 将N个式子代入一点超前差分公式中，即可得出关于N+1个系数的方程组. 求解该方程组即可得到N+1个数据点的一点超前公式. 使用基于泰勒级数展开的推导方法所得到的二至十六个数据点的一点超前公式以及截断误差与文献[5]中给出的一致，这使得一点超前公式的理论基础更加完善.

另外，计算机数值实验表明，一点超前公式可以取得较好的一阶导数估计精度[5]. 附录中给出了利用一点超前差分公式来近似目标点的一阶导数的Matlab程序代码. 只要给出N+1个等间距数据点的函数值及间距，即可求出第N个点的一阶导数近似值.

2 一点超前差分公式

若x0,x1,…,xn为采样区间[a,b]上n+1个互不相同的等间距数据点，即xi+1-xi=h，i=0,1,…,n-1，其中h为采样间隔常数，则未知目标函数f(x)的一阶导数的一点超前差分公式为[5]

表1 二至八个数据点的等间距一点超前数值差分公式

3 基于泰勒级数展开的推导过程

定理1一阶导数的等间距一点超前差分公式的形式为

f′(xn-1)≈a0f(x0)+a1f(x1)+…+an-1f(xn-1)+anf(xn)，

(1)

系数a0,a1,…,an可以由泰勒级数展开来推导并求解线性方程组得出.

证f(x)在点xn-1的泰勒展开式为

(2)

其中c介于xn-1与x之间.

对于0≤k≤n(k≠n-1)，将xk=xn-1+(k+1-n)h代入(2)中，可以得出n个等式

其中ck介于xn-1与xk之间.

将以上n个等式代入(1)中，可得

f′(xn-1)≈ (a0+a1+…+an-1+an)f(xn-1)

+(1-n)ha0+(2-n)ha1+…+(-1)han-2+hanf′(xn-1)

(3)

令(3)右边的f′(xn-1)的系数等于1，f(xn-1),f″(xn-1),…,f(n)(xn-1)的系数于0，可得出关于a0,a1,…,an的线性方程组

由此可以求出一阶导数的等间距一点超前差分公式中的系数. 通过观察可知，该公式的截断误差为

(4)

当n=1时，一点超前差分公式的形式为f′(x0)≈a0f(x0)+a1f(x1)，此时关于a0,a1的方程组及其解为

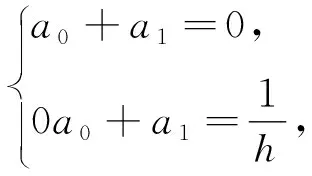
因此f′(x0)≈f(x1)-f(x0)/h. 由(4)可知截断误差为

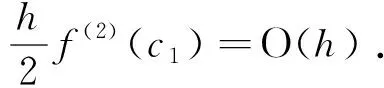
当n=2时，一点超前差分公式的形式为f′(x1)≈a0f(x0)+a1f(x1)+a2f(x2)，此时关于a0,a1,a2的方程组及其解为

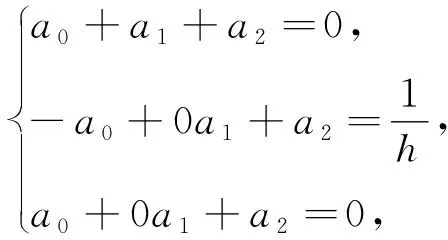
因此f′(x1)≈f(x2)+0f(x1)-f(x0)/(2h)，截断误差为

当n=3时，一点超前差分公式的形式为

f′(x2)≈a0f(x0)+a1f(x1)+a2f(x2)+a3f(x3)，

此时关于a0,a1,a2,a3的方程组及其解为

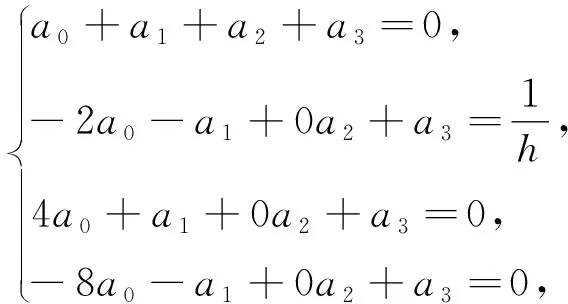
因此f′(x2)≈2f(x3)+3f(x2)-6f(x1)+f(x0)/(6h),截断误差项为

可以看出，基于泰勒级数展开推导出来的一点超前差分公式及其截断误差，与表1给出的完全一致. 对于n>3的情况，可使用附录中给出的Matlab程序来验证. 另外，八至十六个数据点的等间距一点超前差分公式可参考文献[5].

这样，我们就从另一个方面证明了一点超前公式的正确性.

4 结 论

传统的有限差分公式包括前向差分、后向差分和中间差分公式. 使用这些公式可以有效地近似未知函数在目标点的近似值. 但是，对于靠近边界的目标点，单边数据点不足，无法应用多点的中间差分公式. 另外，前(后)向差分公式无法适应未知函数在目标点的导数的加速变化. 一点超前数值差分公式可以有效地解决上述问题，其准确性也已经得到了验证.

本文给出了基于泰勒级数展开的对一点超前差分公式的推导过程. 通过对采样点应用泰勒级数展开式，我们得出了关于一点超前公式中的系数的线性方程组. 最后，我们还给出了自动列出并求解该方程组的Matlab程序. 总而言之，本文从另一个角度，进一步证实了一点超前差分公式的有效性和正确性.

5 附 录

以下给出求一点超前公式系数及目标点的一阶导数近似值的Matlab程序.

%输入：

% F: 包含n+1个采样函数值的向量，即[f(0),f(1),...,f(n)]′

% h: 采样间隔常数

%输出：

% d: 第n-1个点的一阶导数近似值，即f′(n-1)

% A: 包含n+1个系数的向量，即[a0,a1,...,an]′

function [d,A]=oneNodeAhead(F,h)

n=size(F,1)-1;

Y=zeros(n+1,1);

Y(2,1)=1/h;

B=ones(n+1,n+1);

for j=1∶(n+1)

b=1;

for i=2∶(n+1)

if j==n

B(i,j)=0;

else

b=b*(j-n);

B(i,j)=b;

end

end

end

A=BY;

d=A'*F;

end

[参 考 文 献]

[1] Li Jian-ping. General explicit difference formulas for numerical differentiation[J]. Journal of Computational and Applied Mathematics，2005，183(1)：29-52.

[2] John H M，Kurtis D F. 数值方法(MATLAB 版)[M] .4 版.周璐，陈渝，钱方，等译. 北京：电子工业出版社，2009.

[3] 李建良，蒋勇，汪光先. 计算机数值方法[M]. 南京：东南大学出版社，2000.

[4] Ishtiaq R K，Ryoji O. Taylor series based finite difference approximations of higher-degree derivatives[J]. Journal of Computational and Applied Mathematics，2003，154(1)：115-124.

[5] 张雨浓，陈宇曦，陈锦浩，殷勇华. 一点超前数值差分公式的提出、研究与实践[J]. 中山大学学报(自然科学版)，2012，51(2)：1-5.

[6] 张雨浓，郭东生，徐思洪，李海林. 未知目标函数之一阶数值微分公式验证与实践[J].甘肃科学学报，2009，21(1)：13-18.

[7] 白晓东. Taylor公式逼近精度的研究[J]. 大学数学，2004，20(4)：108-110.