用矩阵方程法求解循环卷积的改进算法
李亚峻, 李 红, 何 静, 张春霞
(1. 天津科技大学电子信息与自动化学院,天津300222; 2. 吉林建筑工程学院电气与电子信息工程学院,长春130022)
1 引 言
伴随着计算机技术、信息技术和微电子学的飞速发展,数字信号处理的理论与技术日益成熟,其应用领域不断扩大,其在电子消费产品、通信系统、生物医学、地质勘探等领域均有广泛应用[1-4].
经典的数字信号处理采用时域和频域两类方法分析和处理离散时间信号通过线性时不变系统的问题.循环卷积是数字信号处理时域分析方法中的重要内容.M点有限长序列x(n)(0≤n≤M-1)与N点有限长序列h(n)(0≤n≤N-1)的L点循环卷积yc(n)(0≤n≤L-1)的定义为[6]

(1)
或者

(2)
其中L≥max(M,N),M,N,L∈正整数.RL(n)是矩形脉冲序列,在0≤n≤L-1范围内它的值均为1,在其他n时刻它的值均为0,由RL(n)可知yc(n)的取值范围在0≤n≤L-1.h((n))L代表的是对h(n)以L为周期进行周期延拓,所以它是周期为L的周期序列.
循环卷积的时域求解方法可以分为两类:以m为变量的求解方法和以n为变量的求解方法.以式(1)为例,以m为变量的求解方法的步骤是:
(a) 将序列x(n),h(n)变量代换为x(m),h(m)之后补零,使二者的长度均为L,可用x(m)L,h(m)L表示.
(b) 将h(m)L周期延拓为周期序列h((m))L,翻褶为h((-m))L,取其在0≤m≤L-1范围内的值,得到h((-m))LRL(m).
(c) 将h((-m))LRL(m)循环右移到h((n0-m))LRL(m),其中n0是0≤n≤L-1范围内的一个值.
(d) 将序列x(m)与序列h((n0-m))LRL(m)在0≤m≤L-1范围内对应位相乘后的值加起来,得到yc(n0).
(e) 将n从0到L-1依次取值,仿效(c),(d)两步,求出全部yc(n)的值.
以m为变量的求解方法又被细分为同心圆法[5,6]、图解法[5,7,9,11]、列表法[5]、矩阵方程法[5,8,11,12]等.同心圆法是将x(m)与h((-m))LRL(m)的值按对应位置写在两个同心圆上,将后者循环移位(又被形象地称为圆周移位)后与前者对应位相乘后相加;图解法是画出上述求解步骤中各序列的波形,图解法与同心圆法的共同特点是直观、形象,但是画图即耗时又占纸面,在实际计算中并不可取;列表法是图解法的数字化形式;矩阵方程法构造了L×L维矩阵和L维列向量.由于L≥max(M,N),导致L×L维矩阵和L维列向量中存在冗余项,使矩阵方程变得复杂了.当两序列长度差较大或者L比max(M,N)大得多时,这个问题更加突出.
本文将提出矩阵方程法的改进算法,消除矩阵方程中的冗余项.
2 用矩阵方程法求解循环卷积
列写矩阵方程的关键是正确写出h((-m))LRL(m)的值,这里以图例的形式找到它与h(m)L之间的关系.
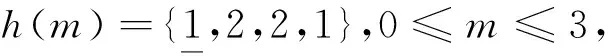
解如图1所示,
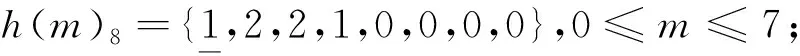
(b) 将h(m)8以8为周期进行周期延拓;
(c) 将h((m))8以m=0为对称中心翻褶为h((-m))8;
(d) 截取h((-m))8在0≤m≤7范围(一个完整周期)内的值,得到h((-m))8R8(m).

图1 h((-m))8R8(m)与h(m)8的关系
仔细观察图1(d)与图1(a),可以发现h((-m))8R8(m)与h(m)8之间的关系是
h((-m))8R8(m)

(3)
推广到更一般的情况,
h((-m))LRL(m)

(4)
也就是使h(m)L中的h(0)保持不变,h(1)至h(L-1)倒序排列.
将h((-m))LRL(m)循环右移一位,即把h((-m))LRL(m)最右端的值移到最左端,其他值向右移一位,可得h((1-m))LRL(m).依此类推可得h((n-m))LRL(m),0≤n≤L-1.
序列h((n-m))LRL(m)与x(m)(0≤m≤L-1)的长度均为L,将这两个等长的序列对应位相乘后的值加起来,实现的正是矩阵乘法运算,矩阵方程如下:
(5)
其中x(m)L以L维列向量的形式放在方阵的右侧,h((-m))LRL(m)及其循环右移序列
h((n-m))LRL(m)(1≤n≤L-1)
构成L×L维的方阵,h((-m))LRL(m)是方阵的第一行,其余各行依次通过对上一行循环右移一位得到.
3 矩阵方程法的改进算法
由于x(n)只在0≤n≤M-1范围内有非零值,而L≥max(M,N),所以式(5)最右侧的列向量中的x(M)至x(L-1)均为零,它使得L×L维方阵中的后L-M列在矩阵运算中并没有起作用,即
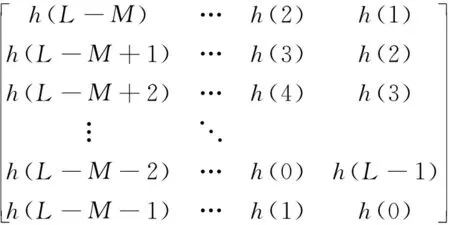
(6)
(7)
简化后的矩阵方程的构成规律是:矩阵方程中的列向量就是有限长序列x(n)(0≤n≤M-1);L×M维矩阵中的第一列就是h(n)L,其余各列依次为前一列循环下移一位的结果,矩阵的列数等于序列x(n)的长度M,所以是L×M维的矩阵.
若用式(2)求解循环卷积,其简化的矩阵方程为
(8)
由于h(n)(0≤n≤N-1)的长度为N,所以这里的矩阵是L×N维的,其第一列就是x(n)L,其余各列依次为前一列循环下移一位的结果.
建议将x(n)与h(n)中较短的序列作为列向量,将较长的序列作为循环下移的对象构成矩阵,以进一步简化运算.
4 实例验证
例2已知

求8点循环卷积yc(n)=x(n)⑧h(n).
解由于L=8,将x(n),h(n)补零到8点长,
分别用式(5)和式(7)的矩阵方程法求解,
所以
可见,前者含有冗余项,而后者不含冗余项.
5 结 论
本文对以m为变量求解循环卷积的矩阵方程法进行了分析,提出了改进算法,给出了矩阵方程内部各列的构成规律,使矩阵中不再含有冗余项,从而简化了矩阵方程.通过实例对矩阵方程法及其改进算法进行了比较,可见改进算法更加简便、有效.
[参 考 文 献]
[1] Marin-Hurtado J I,Anderson D V. FFT-based block processing in speech enhancement: potential artifacts and solutions[J]. IEEE Transactions on Audio,Speech,and Language Processing,2011,19(8): 2527-2537.
[2] Candan C. On the eigenstructure of DFT matrices [DSP education][J]. IEEE Signal Processing Magazine,2011,28(2): 105-108.
[3] Wonzoo Chung. A matched filtering approach for phase noise suppression in CO-OFDM systems[J]. IEEE Photonics Technology Letters,2010,22(24): 1802-1804.
[4] Reeves S J. Fast image restoration without boundary artifacts[J]. IEEE Transactions on Image Processing,2005,14(10): 1448-1453.
[5] Sanjit K Mitra. Digital signal processing—a computer-based approach[M]. 3版. 北京: 清华大学出版社,2006.
[6] 王华奎. 数字信号处理及应用[M]. 2版. 北京: 高等教育出版社,2009.
[7] 郑君里,应启珩,杨为理. 信号与系统(下)[M]. 2版. 北京: 高等教育出版社,2004.
[8] 高西全,丁玉美. 数字信号处理[M]. 3版. 西安: 西安电子科技大学出版社,2010.
[9] 程佩青. 数字信号处理教程[M]. 3版. 北京: 清华大学出版社,2007.
[10] 吴镇扬. 数字信号处理[M]. 北京: 高等教育出版社,2004.
[11] 陈后金. 数字信号处理[M]. 2版. 北京: 高等教育出版社,2008.
[12] 丁玉美. 高西全. 《数字信号处理》学习指导[M]. 3版. 西安: 西安电子科技大学出版社,2010.

