改进欧拉格式求解随机微分方程的收敛性

贾俊梅

(内蒙古工业大学理学院工科数学部，呼和浩特010051)

1 引 言

随着随机微分方程越来越广泛地应用于物理、金融、生物和经济等各个领域中,对随机微分方程解的本身及其解形态的研究就显得十分重要. 但是大多数情况下,与常微分方程情形类似，其解析解不易求出. 当无法给出方程解的解析表达式时，也可通过考察解过程的各阶矩的性质从而把握解的形态. 例如,Ding Xiao-hua等研究了不同数值方法求解随机微分方程的均方收敛性[1-5]，本文建立了改进的欧拉格式求解随机微分方程的强收敛性定理.

2 改进欧拉格式

考虑Ito型随机微分方程(SDE)

dx(t)=f(x(t),t)dt+g(x(t),t)dw(t),x(0)=x0，t∈[0,T],

(1)

其中f(x(t),t),g(x(t),t)分别称为偏移系数和扩散系数,且满足Lipschitz条件和线性增长条件. 即对于任意的x,y∈,t∈[0,T]，存在常数K1>0,K2>0使得

f(x,t)-f(y,t)2∨g(x,t)-g(y,t)2≤K1x-y2,

(2)

f(x,t)2∨g(x,t)2≤K2(1+|x|2).

(3)

给定的步长h>0,用改进的欧拉格式计算方程(1),近似解yk≈x(tk),tk=kh,y0=x0. 具体的差分格式如下：

预估格式：

(4)

改进格式：

(5)

(6)

(7)

(8)

这里IF(t)为示性函数

(9)

3 改进欧拉格式的均方收敛性

引理3.1如果h<1并且满足方程(3)，那么存在两个正常数A,B使得

(10)

证方程(4)两边平方，得

由基本不等式2ab≤a2+b2和方程(3),

+2ykg(yk,tk)Δwk+2f(yk,tk)g(yk,tk)hΔwk

≤(1+h+K2h+K2Δwk2+K2h2)|yk|2+(K2h+K2h2+K2Δwk2)

+2ykg(yk,tk)Δwk+2f(yk,tk)g(yk,tk)hΔwk,

即

引理3.2当h<1并且满足方程(3),那么存在两个正常数G,F，使得

(11)

证由方程(5)两边平方,

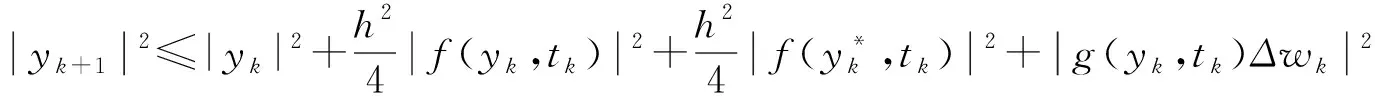
(C=1+K2+AK2,D=BK2+3K2).

由Grownwall不等式得

引理3.3如果h<1并且满足方程(2)，(3)，那么存在两个正常数H，I使得

E|y(t)-z1(t)|2≤Hh, E|y(t)-z2(t)|2≤Ih.

(12)

证对于任意的t∈[0,T]，存在非负整数k,当t∈[kh,(k+1)h]，由(7)，(8)得到

根据基本不等式(a+b+c)2≤3|a|2+3|b|2+3|c|2，(3)及引理(2.1)，

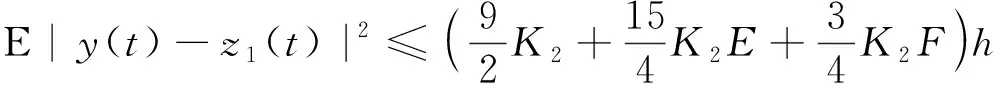
由(5)得到

类似得到

E|z1(t)-z2(t)|2=(4+4G)K2h,

E|y(t)-z2(t)|2≤2E|y(t)-z1(t)|2+2E|z1(t)-z2(t)|2

定理x(t)是方程(1.1)的精确解,y(t)是由方程(9)给出的数值解,f,g满足方程(2)，(3)，并且h<1假设存在常数K3，

f(x,s)-f(x,t)2∨g(x,s)-g(x,t)2≤K3(1+|x|2)|s-t|，

(13)

对于任意的s,t∈[0,T],x∈，那么存在正常数M使得

(14)

证由(1)和(9)得

|x(t)-y(t)|

由基本不等式(a+b+c+d+e+f)2≤6a2+6b2+6c2+6e2+6f2和Hölder不等式，

|x(t)-y(t)|2

由(2)和(13)得,

|x(t)-y(t)|2

由Burkhölder-Davis-Gundy不等式,

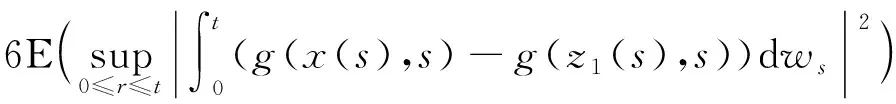
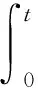
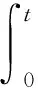
由引理(3.1),(3.2),(3.3)得到如下的式子,

由Gronwall不等式得 ,

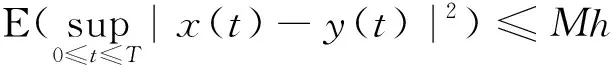
[参 考 文 献]

[1] Ding Xiaohua，Ma Qiang，Zhang Lei. Convergence and stability of the split-step θ-method for stochastic differential equations[J]. Computers and Mathematics with Applications，2010,60:1310-1321.

[2] Fan Zhengcheng，Liu Mingzhu，Cao Wanrong. Existence and uniqueness of the solutions and convergence of semi-implicit Euler methods forstochastic pantograph equation[J]. J.math.Anal.Appl,2007，325:1142-1159.

[3] Xiao Y，Zhang H Y. A note on convergence of semi-implicit Euler methods for stochastic pantograph equations[J]. Computers and Mathematics with Applications，2010,59:1419-1424.

[4] Tian Tianhai，Burrage Kevin. Implicit Taylor methods for stiff stochastic differential equations[J]. Applied Numerical Mathematics,2001,38:167-185.

[5] 刘小清,吴声昌.随机微分方程计算方法及其应用[J]. 计算物理,2002,19(1):1-6.