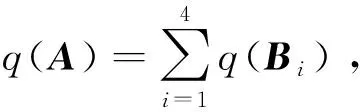实二次型的顺序主子式与惯性指数

王 伟， 张吉林， 严志丹

(塔里木大学信息工程学院， 新疆阿拉尔843300)

1 引 言

一个n元实二次型

定义1子式

称为矩阵A=(aij)n×n的i阶顺序主子式. 为方便起见，补充规定0阶顺序主子式P0=1.

设a0,a1,…,al是非零实数的序列，它的变号数v(a0,a1,…,al)定义为集合{aiai+1∶0≤i≤l-1}中的负数个数. 二次型的正(负)定判别法可以重新表述为：n元实二次型f=X′AX正(负)定当且仅当P0=1,P1,…,Pn全不为零且其变号数为0(n).恰当地定义含零序列的变号数，下面的定理推广了这一结果.

定理1[1]设n元实二次型f=X′AX秩为r. 如果A的r阶顺序主子式Pr≠0，那么f的负惯性指数等于序列P0,P1,…,Pr的变号数v(P0,P1,…,Pr)，其中

(i) 如果PiPi+2≠0且Pi+1=0，规定v(Pi,0,Pi+2)=1；(Gundelfinger法则)

(ii) 如果PiPi+3≠0且Pi+1=Pi+2=0，当PiPi+3>0规定v(Pi,0,0,Pi+3)=2；当PiPi+3<0规定v(Pi,0,0,Pi+3)=1；(Frobenius法则)

(iii) 如果PiPi+4≠0且Pi+1=Pi+2=Pi+3=0，当PiPi+4>0规定v(Pi,0,0,0,Pi+4)=2；当PiPi+4<0，v(Pi,0,0,0,Pi+4)不能确定；

(iv) 如果存在k≥4满足PiPi+k+1≠0且Pi+1=Pi+2=…=Pi+k=0，那么v(Pi,0,…,0,Pi+k+1)不能确定.

注 当P0,P1,…,Pr任意相邻两项不全为零时，定理1的证明可见[2-4].

例1设秩为8的实对称矩阵A的0～8阶顺序主子式依次为 1，-2，0，0，0，-4，0，0，3. 根据定理1，知v(1,-2)=1,v(-2,0,0,0,-4)=2,v(-4,0,0,3)=1，故序列P0,P1,…,P8的变号数v=v(1,-2)+v(-2,0,0,0,-4)+v(-4,0,0,3)=4. 从而A的负惯性指数为4.

本文给出定理1的简单证明，对于定理1中所指出的不能确定情形，给出了符合所给顺序主子式序列的二次型的所有可能类型.

2 特殊的顺序主子式符号序列

命题1设n≥2，则

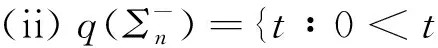
证当n=2时，由Σn的定义，易知

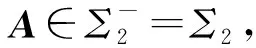
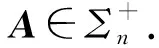
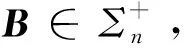
可以类似地证明(ii).

利用命题1，注意到n=1时的明显性，容易得到表1.

表1 具有1至n-1阶零顺序主子式的n阶可逆实对称矩阵负惯性指数与行列式符号的关系

解不难算出|A|=1>0,P1=P2=P3=0.查表1，可知q(A)=2(对应于定理1中变号数第3条规定的前半部分).

3 一般的顺序主子式符号序列

我们把主对角线上全是1的上三角矩阵称为单位上三角矩阵[5].

引理1[5]设A为实对称矩阵，T为单位上三角矩阵，而B=T′AT，则A与B对应的顺序主子式有相同的值.

命题2设实对称矩阵A的秩为r，其非零顺序主子式分别为Pi0=1,Pi1,Pi2,…,Pis，0=i0

证对s用归纳法. 当s=0时，r=0，A为零矩阵，命题显然成立.

假设命题对s-1是成立的. 令

显然B1满足命题结论的要求.

将A分块成

由条件知B1=Pi1≠0. 令

易知D1的秩R(D1)=r-R(B1)=r-i1.

由归纳假设，知存在n-i1阶单位上三角矩阵T2，使得

其中Bk(2≤k≤s)是可逆矩阵，阶数为(ik-i1)-(ik-1-i1)=ik-ik-1，

且当ik-ik-1≥2时Bk的1至ik-ik-1-1阶顺序主子式全为零.

4 结 论

由于准对角矩阵的负惯性指数等于每个对角块的负惯性指数之和，由命题1，2可得定理1. 实际上，利用表1的最后三行，对于定理1中“不能确定”的情形，可以给出所有可能的负惯性指数.

例3设非奇异的10阶对称矩阵A的顺序主子式P0,P1,…,P10的符号序列为+，-，0,0,0,0,-,-,0,0,+，求其可能的负惯性指数.

解注意到A的非零主子式的阶数依次为0，1，6，7，10，由命题2知，存在单位上三角矩阵T，使得

[参 考 文 献]

[1] Browne E T. On the signature of a quadratic form[J]. Annals Math. 1928，30 (1/4):517-525.

[2] Franklin P. A theorem of Frobenius on quadratic forms[J]. Bull. Amer. Math. Soc，1927,33(4): 447-452.

[3] 王世芳，周开瑞. 实二次型的顺序主子式与符号差[J]. 四川师院学报(自然科学版)，1983(3):86-94.

[4] 刘长安,刘效丽. 实二次型的符号差[J].数学通报,1992(11)：33-36.

[5] 杨子胥. 高等代数习题解(修订版 下册)[M].济南：山东科学技术出版社，2004：32.