单调有界数列必有极限定理的一个直接证明及其作用
郑 权, 张彩霞, 郭秀晖
(北方工业大学理学院,北京100144)

实际上,本文仿照教材[2]和文[8]利用实数十进制证明确界原理的方法,就能够直接构造性地证明单调有界定理.由此会产生如下良好效果:可以解答在高等数学的讲授和学习过程中时常出现的由没有证明单调有界原理所带来的疑惑,并且以此为立足点易得数列极限存在性的两个重要准则的等价关系:
单调有界原理⟺柯西收敛准则,
从而使得高等数学教材和教学中的数列极限理论成为自身完备;还可以在数学分析教学中回顾实数的无限小数表示并发扬构造性地证明确界原理的技巧,而且补充展示关于实数系完备性的这个立足点,进一步易见如下的循环论证:
单调有界定理⟹区间套定理⟹有限覆盖定理
⟹聚点定理⟹柯西收敛准则⟹确界原理⟹单调有界定理.
为了以下讨论的需要,我们把任一实数表示为一个十进制无限小数.只需把有限小数(包括整数)也表示为无限小数,规定:对于正有限小数x=a0.a1a2…an,其中ai∈{0,1,…,9},i=1,2,…,n,an≠0,a0为非负整数,记x=a0.a1a2…(an-1)99…9…;对于正整数x=a0,记x=(a0-1).99…9…;对于负有限小数(包括负整数)y,先把-y表示为无限小数,再在其前加负号;对于数0,记0=0.00…0….
下面我们就利用实数的十进制无限小数表示和极限的定义证明实数系中单调增加有上界的数列xn必存在极限.当数列xn单调下降时,考察{-xn}即可.注意到单位长度作十等分与十进制实数的度量之间的关系,我们不难证明如下的引理:
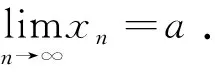
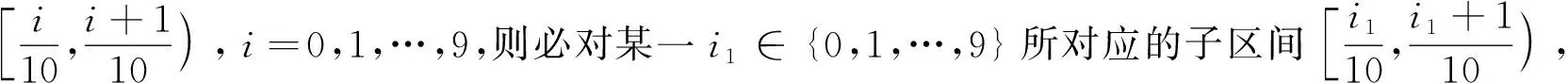
否则,永远有点xN落在下一个子区间上,但只有10个子区间,就导致矛盾.

依此类推,

定理若数列xn满足x1≤x2≤…≤xn≤… 综上,我们给出“单调有界数列必有极限”的一个深刻而简洁的新证明,并指出该定理在实数完备性和数列极限理论中的基础作用.这可让数学系的学生从新视角理解实数完备性,让其它系的学生快速了解该定理的一种证明,有益于相应的学生更好地理解和运用此定理. [参 考 文 献] [1] 同济大学数学系.高等数学[M].6版. 北京:高等教育出版社,2007. [2] 华东师范大学数学系.数学分析[M].4版. 北京:高等教育出版社,2010. [3] 王绵森, 马知恩.工科数学分析基础[ M].2版. 北京:高等教育出版社,2006. [4] 倪谷炎, 白敏.关于Weierstrass定理的证明[J].高等数学研究,2009,12 (5):43-44. [5] 刘利刚.实数系基本定理等价性的完全互证[J].数学的实践与认识,2008,38(24):246-252. [6] 王嘉谋.单调有界准则的新证明[J]. 包头钢铁学院学报, 1996,15 (4):8-10. [7] 赵振学.单调有界数列一定收敛的新证法[J]. 兰州石化职业技术学院学报,2002,2 (4):14. [8] 杜珣.在“高等数学”首堂课上讲授实数完备性[J].高等数学研究,2004,7 (4):8-9.

——丘成桐

