混合型随机变量期望的求法及应用
何晓霞, 侯 萱, 李春丽
(武汉科技大学理学院,湖北武汉430065)
1 问题的提出
计算随机变量函数的期望是在运用期望值进行决策时经常碰到的问题,在经典的概率论教材里都有随机变量函数的数学期望的计算方法.
定理1.1[1]设Y是随机变量X的函数:Y=g(X)(g是连续函数).
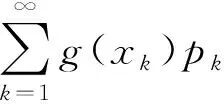
(1.1)
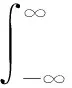

(1.2)
该定理为我们提供了一个计算随机变量函数的期望的较简单的求法,因为计算期望的时候并不需要求出Y的分布律或者密度函数.运用这个定理,我们来计算下面的例子.
例1.1设随机变量X在区间[-π,π]上服从均匀分布,求E[min(|X|,1)].
解X的概率密度函数为
故

这个例子之所以能运用定理,是因为
因此min[|X|,1]是随机变量X的连续函数,符合定理的假设条件.虽然定理中只需假设复合给随机变量的函数g连续即可,即g(X)是什么类型的随机变量实际上并未做任何要求.事实上,例1.1中的min[|X|,1]是一个混合型随机变量.这是因为
P(min[|X|,1]≤x) =1-P(min[|X|,1]>x)=1-P(|X|>x,1>x)
(1.3)

2 混合型随机变量期望的一般求法
要找到混合随机变量期望的一般求法,首先要将离散型和连续型随机变量的期望的计算方法进行统一.为此,需要用到Stieltjes积分.若随机变量X的分布函数为F(x),类似于连续型随机变量的场合,做分割x0 定义2.1[2]若随机变量X的分布函数为F(x),则定义 (2.1) 为X的数学期望.这里要求积分绝对收敛,否则数学期望不存在. 按照上述数学期望的定义,则可以根据Stieltjes积分的定义来计算混合型随机变量的数学期望.一般地,若混合型随机变量的分布函数有可列个跳跃间断点{xi;i≥1}(这一点是可以做到的,由于分布函数是单调的,所以它的间断点至多可列),则 (2.2) 其中I为分布函数F(x)连续且可导的区域,f(x)为可导区域上分布函数F(x)的导函数.再回到第一节中的例1.1,由(2.2)式, 所得结果与运用定理计算的结果是相同的,为何为出现这样的结果?事实上,(2.1)式可以同时用来计算离散型和连续型随机变量的积分.用测度论的语言来说,数学期望是特殊的测度空间——概率空间上的积分. 定义2.2[3]如果概率空间(Ω,I,P)上可测函数X的积分存在,则说它的数学期望存在,并定义X的数学期望为 (2.3) (2.1)和(2.3)是等价的,文献[4]对这两种定义的等价性进行了详细的探讨.有了抽象空间中随机变量期望的定义,则有如下定理. 定理2.1[3]设X是概率空间(Ω,I,P)上的随机变量,其分布函数为F, 则对任何(,B())上的可测函数g,g(X)是(Ω,I,P)的可测函数,而且只要 之一端有意义,另一端也有意义且等式成立. 混合型随机变量在实际应用中的大量存在的,这里主要讨论混合型随机变量期望在保险精算中的应用.人们向保险公司投保来规避损失,而保险公司本身为了规避风险,它也可以选择再保险公司.目前常见的两种再保险方法为比例再保险和超额损失再保险.所谓超额损失再保险,即保险公司和再保险公司约定一个值M,若索赔额变量X不超过M,则损失全部由保险公司承担;若索赔额X超过M,则超出部分由再保险公司承担,即保险公司承担的索赔额为Y=min(X,M),再保险公司承担的索赔额为Z=max(0,X-M).显然这两个随机变量都是混合型的,若索赔额索赔随机变量X的分布函数为F,则 在精算过程中常常要需要计算索赔额的各阶矩,通过前述方法即可计算得 若X服从均值为100的指数分布,则 [参 考 文 献] [1] 盛骤,谢式千,潘承毅. 概率论与数理统计[M]. 3版. 北京: 高等教育出版社,2001. [2] 李贤平. 概率论基础[M]. 2版. 北京: 高等教育出版社, 1997. [3] 程士宏. 测度论与概率论基础[M]. 北京: 北京大学出版社,2004. [4] 何晓霞. 数学期望的两种定义及其等价性[J]. 大学数学, 2013, 29(3): 91-93. [5] David C M Dickson. Insurance risk and ruin[M]. Cambridge:Cambridge University Press, 2005.

3 混合型随机变量期望的应用


