求矩阵Jordan标准形的一种新法
全洪正, 黄小英
(衡阳师范学院南岳学院数学与计算科学系,湖南衡阳421008)
1 引 言
Jordan标准形不仅在矩阵理论上而且在工程应用上都是十分重要的.在矩阵方程论,矩阵函数论,常微分方程,现代控制论以及模式识别都有着它的应用.
Jordan标准形的求法在国内外已有较完善的研究结果.例如文献[1]通过构造λ-矩阵、不变因子及初等因子理论,得到了求矩阵Jordan标准形的初等因子法;文献[2]主要讨论了不可以对角化的线性变换的结构,得到了求矩阵Jordan标准形的空间分解法;文献[3]参考可逆矩阵的求法提出了求矩阵Jordan标准形及过渡矩阵的行列互逆初等变换法;文献[4]通过求矩阵的特征向量及其循环向量,从而更快地得出了矩阵的若当形,并附带得出矩阵的演化矩阵.
然而,初等因子法是通过构造λ-矩阵理论,利用λ-矩阵的初等变换方法计算已知矩阵的不变因子和初等因子,即而得到Jordan标准形,但现有的λ-矩阵初等变换方法对阶数较高的矩阵计算非常繁琐.空间分解法一般是先把空间v分解成φ的不变子空间直和,再在每个不变子空间里找到一个适当的基,使得不变子空间中的φ在该基下的矩阵为一个Jordan矩阵.一般认为要通过空间分解法找到矩阵的Jordan标准形要解决以下两个问题:第一如何把空间v分解成φ的不变子空间直和?第二如何在每个不变子空间里找到一个适当的基,使得不变子空间中的φ在该基下的矩阵为一个Jordan矩阵,而要解决这二个问题的难度也非常大.这样,上述二法一般也只是在理论上说明可行,但具体应用起来非常困难.文献[3]讨论了行列互逆初等变换法的本质与初等因子法无异,对阶数较高的矩阵计算起来同样非常繁琐.文献[4]研究的循环向量法虽对阶数较高的矩阵计算不繁琐,但要通过解方程去求线性无关的特征向量,而高斯消元法对多元方程的计算也是通过矩阵变换来实现,则于多元方程的计算仍很复杂.
有鉴于此,本文拟先求出矩阵A的特征值λi(i=1,2,…,s)的j次幂初等因子的长度lij,再利用lij得到矩阵A的不变因子一般式,最后通过不变因子与初等因子关系,得到了求矩阵Jordan标准形的另一方法.
2 预备知识
本节目的是给出与证明一个计算矩阵的秩的公式,同时为了下文讨论的方便,引述一些相关的基本结论.
设A∈n×n,则存在可逆矩阵T∈n×n,使
Jordan矩阵与对角矩阵的差别仅在于它的上对角线(与主对角线平行的上面一条对角线)的元素是1或0,因此它是一个特殊的上三角矩阵.显然,Jordan块本身就是一个Jordan矩阵.对角矩阵也是一个Jordan矩阵,它的每个Jordan块是1阶的.对于矩阵的Jordan标准形. 我们要重点解决两个方面问题:一方面,对于复数域P中任一n阶矩阵都有Jordan标准形;另一方面,给出一个方法,对任何一个n阶复数矩阵A,按照这个方法可以求得它的Jordan标准形J.或者更进一步,求出一个n阶可逆复数矩阵T,使得T-1AT=J.在默认第一个问题已成立的情况下,该文尝试着一种新方法去解决第二个问题.
为了以下讨论的方便,我们列出一些基本记号和已知结果以便后述定理的证明.
定义2.1设λi是n阶方阵A的一个特征值.若特征值λi的j次幂初等因子有lij个,则称lij为特征值λi相对于j次幂初等因子的长度.
定义2.2设λi是n阶方阵A的一个特征值,若存在最小正整数m,使得
rank(λiE-A)ri=rank(λiE-A)ri+m
成立,则称ri为特征值λi的秩指数,记为ri(A)=ri.
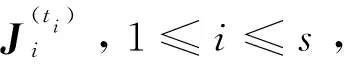

3 主要结论及证明
在本节中,我们将给出求矩阵Jordan标准形新方法的一些结论.
定理3.1对任意n阶方阵A,若特征值λi的j次幂初等因子的长度为lij,则
lij=rank(λiE-A)j-1-2rank(λiE-A)j+rank(λiE-A)j+1,
其中rank(λiE-A)0=n.
在证明这个结论之前,先给出如下引理.
引理3.1设A为复数域上的n阶方阵.若λi是A的一个特征值,则对任意正整数m(1≤m≤ri),有
证因为A=T-1JT,T是某可逆矩阵,所以λiE-A=T-1(λiE-J)T,从而(λiE-A)m=T-1(λiE-J)mT.于是rank(λiE-A)m=rank(λiE-J)m.记E(tk)(k=1,2,…,s)为tk阶单位矩阵,因为
所以

当k=i时,
所以
从而
综上,根据m与j的关系归纳得
定理3.1的证明对A的任一特征值λi,由引理3.1可知
其中i=1,2,…,s;j=1,2,…,n.所以
因此,
lij=rank(λiE-A)j-1-2rank(λiE-A)j+rank(λiE-A)j+1.
定理3.2设λi是n阶方阵A的一个特征值.如果特征值λi的秩指数为ri,相对于ri-kij次幂初等因子长度为li,ri-kij,那么
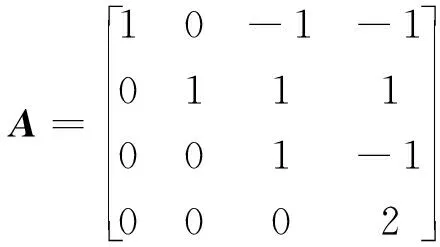
(i) 若0≤kij dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj. (ii) 若kij=ri且1≤j≤n-(li,ri+li,ri-1+…+li,ri-kij+1),则A的不变因子为 dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj, 其中i=1,2,…,s;j=1,2,…,n;kij∈. 证设一个n级矩阵A的特征值所对应的各次因式及个数为已知.在全部的一次因式中将同一个特征值所对应的一次因式(λ-λi)(i=1,2,…,s)的方幂按降幂排列,而且当这些初等因子的个数不足n时,就在后面补上适当个数的1,使得凑成n个.设所得的排列为 则dn(λ)=(λ-λ1)r1(λ-λ2)r2…(λ-λs)rs. 其次,由A的初等因子可得 dn(λ) =[(λ-λ1)…(λ-λ1)r1(λ-λ2)…(λ-λs)rs] =(λ-λ1)r1(λ-λ2)r2…(λ-λs)rs. 如果dn(λ)≠1,那么dn-1(λ)便是初等因子组中去掉dn(λ)的表达式中出现的初等因子后剩余的初等因子的最小公倍式;又如果dn-1(λ)≠1,那么dn-2(λ)便是初等因子组中去掉dn(λ)和dn-1(λ)的表达式中出现的初等因子后剩余的初等因子的最小公倍式. 显然,如此继续下去,所剩余的初等因子个数不断减少.因此在有限次之后,必然有某一阶不变因子开始为1.于是,我们便可推出如下结论: (i) 若0≤kij dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj. (ii) 若kij=ri且j≤n-(li,ri+li,ri-1+…+li,ri-kij+1),则A的不变因子为 dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj, 其中i=1,2,…,s;j=1,2,…,n;kij∈. 注1 在上述定理3.2的意义下,矩阵A的不变因子dn(λ)可以理解为λE-A的最小多项式的一般情况.因此,如下推论. 推论3.1设A的特征多项f(λ)=|λE-A|=(λ-λ1)t1(λ-λ2)t2(λ-λ3)t3…(λ-λs)ts,其中λ1,λ2,λ3,…,λs互异,则λE-A的最小多项式为 dn(λ)=(λ-λ1)r1(λ-λ2)r2…(λ-λi)ri…(λ-λs)rs. (i) 当0≤kij dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj; (ii) 当kij=ri且j≤n-(li,ri+li,ri-1+…+li,ri-kij+1)时,A的不变因子为 dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj, 其中i=1,2,…,s;j=1,2,…,n;kij∈,则A的Jordan标准形为J. 证由定理3.2可知矩阵A的不变因子一般式为 (i) 当0≤kij dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj; (ii) 当kij=ri且j≤n-(li,ri+li,ri-1+…+li,ri-kij+1)时,A的不变因子为 dj(λ)=(λ-λ1)r1-k1j(λ-λ2)r2-k2j…(λ-λi)ri-kij…(λ-λs)rs-ksj, 其中i=1,2,…,s;j=1,2,…,n;kij∈.显然对应于ri-kij≥1的那些方幂(λ-λi)ri-kij就是A的全部初等因子,即 (λ-λ1),…,(λ-λ1)r1-k1j,…,(λ-λi)r1,…,(λ-λs)rs,k1j∈[0,r1]. 假设对任意特征值λi,对应的初等因子为 (λ-λi),…,(λ-λi)k,…,(λ-λi)ri,k∈[0,ri], 则对应于一个Jordan块是 这些Jordan块构成一Jordan标准形 注2 对矩阵A的某一特征值λi,若其代数重数为1,则不需施行以上步骤,它的初等因子就是(λ-λi). 根据以上所述理论,求一个任意矩阵A的Jordan标准形J的方法如下: 1. 求出A的特征多项式fA(λ)=λE-A; 2. 解方程fA(λ)=0,求出矩阵A的互异特征值λ1,λ2,λ3,…,λs; 3. 对任意一个λi,计算rank(λiE-A)m,直至其不再减少为止,得到特征值λi的秩指数ri,并依据定理3.1计算λj的j次幂初等因子长度lij; 4. 对任意一个λi,首先依据定理3.2计算矩阵A的不变因子dj(λ),然后根据定理3.3得到矩阵的Jordan标准形. 解先求出矩阵A的特征多项式 由此求出了A的特征值λ=1,2.下面计算ri和lij. 当λ1=1时, rank(λ1E-A)=2; rank(λ1E-A)2=1; rank(λ1E-A)3=1. 由定义2.2易知r1=2.由定理3.1可得l11=4-2×2+1=1,l12=2-2×1+1=1. 同理可得:当λ2=2时,r2=1,l21=1. 综上,由定理3.2知 d4(λ)=(λ-1)2(λ-2),d3(λ)=λ-1,d2(λ)=d1(λ)=1. 本文所讨论的方法是从rank(λiE-A)出发,避开λ-矩阵初等变换求得矩阵的不变因子,再利用不变因子与初等因子之间的关系,求出了矩阵Jordan标准形,这大大减小了计算难度,程序性强,便于操作. [参 考 文 献] [1] 北京大学数学系. 高等代数[M]. 3版. 北京:高等教育出版社, 2003: 273-358. [2] 丘维声. 高等代数[M]. 北京: 高等教育出版社, 1996: 267-303. [3] 易福侠, 王金林. 矩阵若当标准化的一种新方法[J]. 大学数学, 2009,25(3): 164-167. [4] 席光明. 避开求初等因子化矩阵为若当形[J]. 零陵师专学报(自然科学版), 1991,13(3): 51-53. [5] 钱吉林, 李海照. 矩阵及其广义逆[M]. 武汉: 华中师范大学出版社, 1988: 273-390.
4 方法步骤
5 应用举例
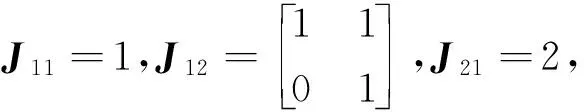
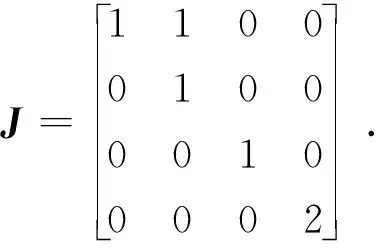
6 结 论

