从射影观点看焦点

周建伟

(苏州大学数学科学学院, 江苏苏州215006)

本文用射影几何观点讨论二次曲线焦点与准线的性质, 有关极点, 极线, 共轭等概念可参阅射影几何教材[1],[2]. 熟悉欧氏几何的读者可以尝试用平面几何的方法证明这些结论, 作进一步的研究.

平面上二次曲线可以是椭圆, 双曲线或抛物线, 把圆看成特殊的椭圆. 本文有些材料取自[2], 例如定理1,3, 为了完整写出了它们的证明. 下面是焦点与准线的射影几何定义.

定义如果过欧氏平面上点F的任意一对关于二次曲线共轭的直线都垂直,那么F叫做二次曲线的焦点,F的极线是准线.

可以证明这样定义的焦点与通常的定义一样, 且焦点总在对称轴上. 下面利用这一射影几何定义讨论二次曲线有关焦点的性质.

定理1设F是二次曲线的一个焦点,T是曲线上弦PQ端点处切线的交点,PQ交F对应的准线于R, 则TF与RF分别是∠PFQ的内外角平分线.

证如图1,ξ是F对应的准线. 易知R的极线是TF, 因此直线FR与TF共轭. 由假设F是焦点,FR与TF垂直.P,Q,S=FT×PQ,R是调和点列,FP,FQ,FS,FR是调和直线. 再由FR与FS垂直, 可知TF与RF是∠PFQ的内外角平分线.

如图2, 如果定理1中二次曲线是双曲线,P,Q分别是双曲线两支上点. 则RF1是∠PF1Q的内角平分线, 而TF1是∠PF1Q的外角平分线.

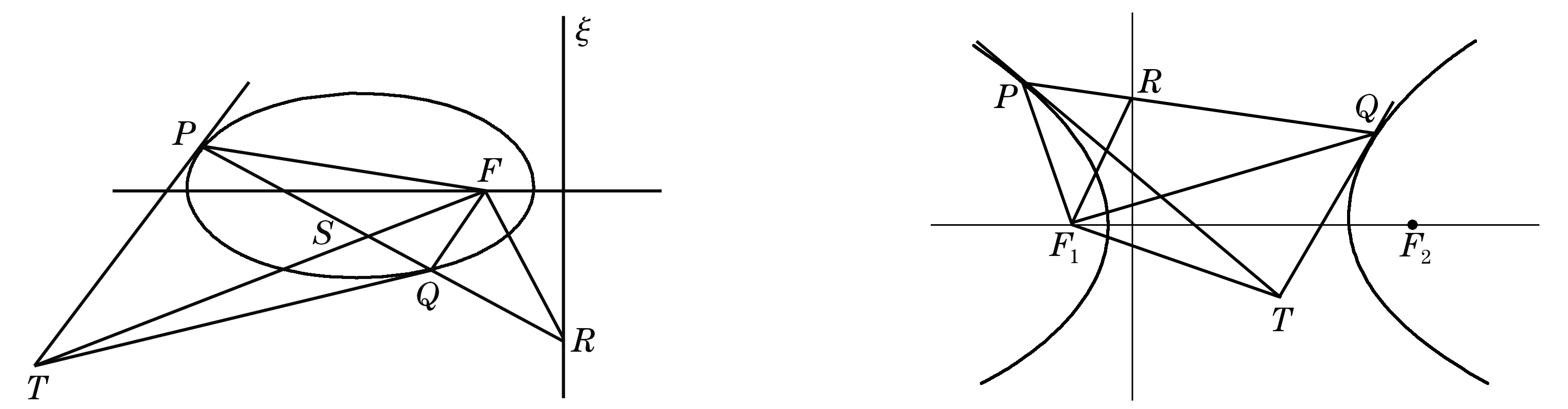
图1 图2

利用定理1容易得到：

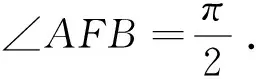
下面的引理在讨论二次曲线焦点的性质时常有用, 证明见[2] p.153例4.

引理2设三角形ABC的三边分别与二次曲线切于D,E,F, 设P为直线EF上任一点, 则直线BP与CP关于二次曲线共轭.

定理3如果三角形的三边都与抛物线相切, 则三角形的三个顶点与焦点四点共圆.

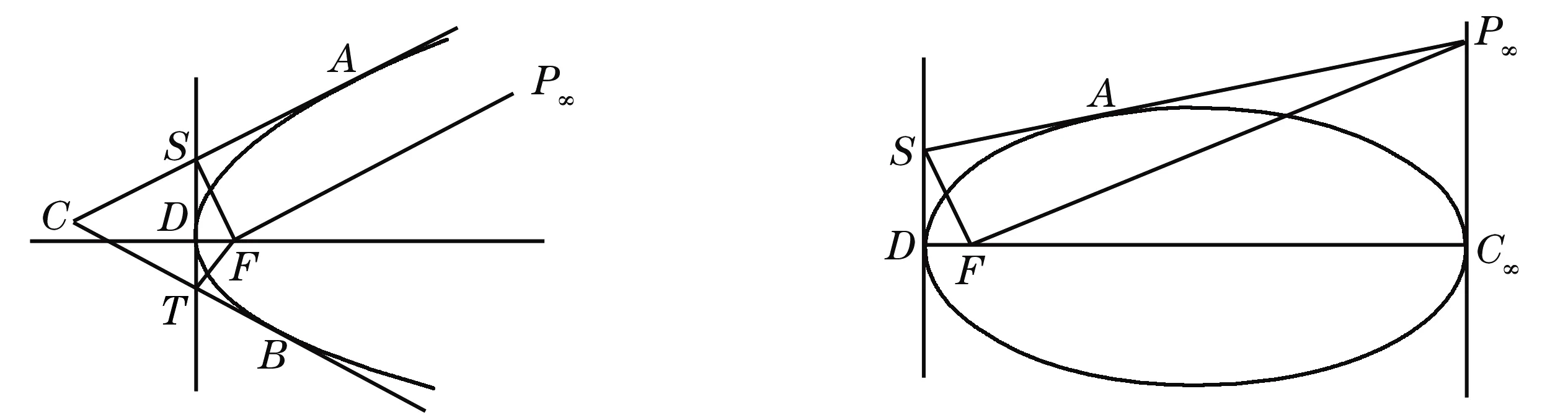
图3-1 图3-2

证如图3-1, 设抛物线上点A,B的切线交于C, 抛物线顶点D处的切线与CA,CB分别交于S,T;F是抛物线的焦点. 先证明C,S,T,F四点共圆. 过F作CA的平行线与CA交于P∞,C∞是抛物线上的无穷远点, 图3-2画出了无穷远直线. 由引理2,SF与FP∞共轭, 而F是焦点,SF与FP∞垂直,SF与CA也垂直. 同理,TF与CB也垂直, 四点C,S,T,F共圆.

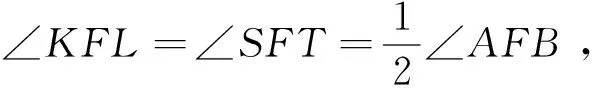
由证明可以得到抛物线焦点的作法:

设抛物线的任一切线η交抛物线的顶点处切线于S, 过S作η的垂线与对称轴的交点F就是焦点.

从定理3的证明还可以得出抛物线焦点的光学性质：

定理4设η是抛物线的任一切线, 直线ξ过η上切点A平行于抛物线的对称轴,F是焦点, 则AF,ξ与η的交角相等.

证如图4, 设E是η与抛物线对称轴DF的交点,S是顶点D处切线与η的交点. 由定理1,SF是∠AFE的角平分线; 从定理3的证明知道,FS垂直于η,所以∠EAF=∠AEF,EFA构成等腰三角形, 这证明了抛物线焦点的光学性质.

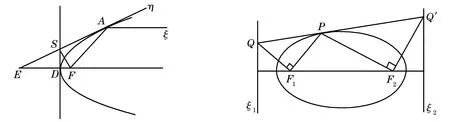
图4 图5

定理5二次曲线的任一切线上切点及它与准线的交点所成线段对焦点张成直角.

证如图5,F1是焦点, 二次曲线上点P处切线与F1对应的准线ξ1交于Q, 则Q与P,F1都共轭,Q的极线是PF1, 所以PF1与QF1共轭. 从焦点的定义可知,QF1与PF1垂直.

下面利用焦点的射影定义推出离心率的概念.

定理6二次曲线上任一点到焦点的距离与它到对应准线的距离之比是一个常数, 称为二次曲线的离心率.

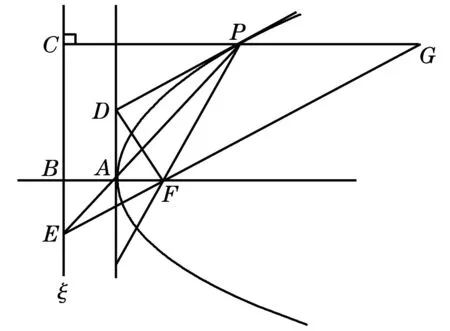
图6

证如图6, 设ξ是焦点F对应的准线.P是二次曲线上任一点,B是ξ与过F的对称轴的交点,C是P向ξ作垂线的垂足,PC∥BF. 如图6, 设A是BF与二次曲线的交点,下证 |PF|∶|PC|=|AF|∶|AB|.

设P,A处切线交于D,AP与ξ交于E,EF交CP于G. 由定理1知道,DF与EF分别是∠PFA的内外角平分线. 在ΔPFG中∠PFG=∠PGF, 从而|PG|=|PF|. 在ΔECG中,BF∥CG, 因此|CP|∶|PF|=|CP|∶|PG|=|BA|∶|AF|是常数.

如果图6中二次曲线是抛物线, 则B,F,A与抛物线上的无穷远点是调和点列,BA=AF,抛物线的离心率等于1. 利用标准方程, 易知椭圆的离心率小于1,双曲线的离心率大于1.利用定理6容易证明:

定理7椭圆上点到两焦点的距离之和是常数; 双曲线到两焦点距离之差是常数.

这样, 上面定义的焦点与中学平面几何定义的焦点是一致的.

定理8设F1,F2是椭圆的焦点,ξ是椭圆过P的切线, 则F1P与F2P和ξ的夹角相等.

证可以用椭圆的离心率证明, 下面的证明可以给出更多的几何信息.

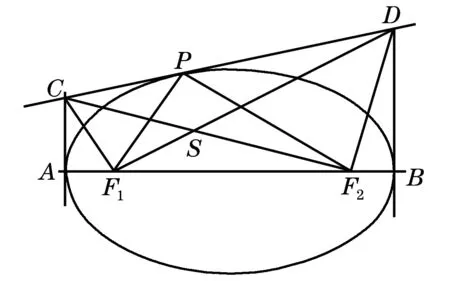
图7

如图7, 过椭圆顶点A,B的切线交ξ于C,D. 由定理1,CF1,DF1与DF2,CF2分别是∠AF1P, ∠BF2P的角平分线. 记S=CF2×DF1,CF2,DF1,PS是ΔPF1F2的角平分线. 由引理2,CF1,DF1;CF2,DF2共轭且垂直, 四点C,F1,F2,D共圆,

∠CDF1=∠CF2F1=∠BDF2,

∠F1CP=∠DF2B=∠PF2D, ∠F2DP=∠AF1C=∠CF1P.

因此ΔCF1P与ΔF2DP相似, ∠CPF1=∠DPF2.

这也给出了椭圆焦点的作法：

设AB是椭圆的长轴,椭圆的任一切线交A,B处切线于C,D, 以CD为直径的圆与AB的交点F1,F2就是椭圆的焦点.

定理9设ξ是双曲线过P的切线, 则F1P与F2P和ξ的夹角相等,F1,F2是焦点.

证如图8, 设A,B是F1F2与双曲线的交点, 过B的切线与ξ交于C. 由定理1,

∠PF1C=∠CF1B, ∠PF2C=∠CF2B,

因此CP也是∠F1PF2的平分线.

定理8, 9分别是椭圆与双曲线焦点的光学性质.

图8 图9

定理10如果抛物线的两切线垂直, 那么两切线上切点的连线通过焦点, 且两切线的交点位于准线上.

证如图9, 设AC,BC是抛物线互相垂直的切线,F是焦点, 过抛物线的顶点D作DF的垂线交AC,BC于G,H. 从定理3的证明可知,HF⊥CB,GF⊥AC,CHFG是矩形. 由定理1,GF与HF分别是∠AFD,∠DFB的平分线, 这证明了A,F,B共线,也证明了C与F共轭. 所以C在准线上,AB过焦点.

也可以证明, 交点在抛物线的准线上的两切线垂直.

定理11抛物线的外切三角形的垂心在抛物线的准线上.

证设ΔABC外切于抛物线. 如果∠BAC是直角,A也是ΔABC的垂心. 由定理10,A在准线上. 设ξ,η是抛物线的两条不垂直的定切线，由Steiner定理, 抛物线的其它切线与ξ,η的交点给出这两直线间的射影映射ψ. 如果 另一切线交ξ,η于B,C, 则ψ(B)=C. 所有与ξ垂直的直线交于一个无穷远点P∞, 同理设Q∞是η的垂线的交点. 由此可得线束P∞与Q∞间的射影映射φ, 它把过B的垂线变为过C的垂线,φ的对应直线的交点就是抛物线相应外切三角形的垂心. 对于抛物线, 无穷远直线是切线, 易知它也是φ的不变直线,φ是透视, 因此它的对应直线交点共线. 分别取垂直于ξ,η的切线, 这时对应三角形的垂心在准线上, 因此φ决定的直线就是准线. 我们证明了抛物线的外切三角形的垂心在抛物线的准线上.

以下是一些有关二次曲线焦点准线的问题, 读者可以试着给出证明.

1. 圆锥曲线的准线与一对不垂直的共轭直径所成三角形的垂心是焦点.

2. 设等边ΔABC的三边与抛物线相切, 三边BC,CA,AB上切点分别是A′,B′,C′, 则AA′,BB′,CC′相交于抛物线的焦点.

3. 证明圆锥曲线过焦点的弦的中点轨迹是同类型的圆锥曲线.

4. 设F,ξ,D分别是抛物线的焦点, 准线, 顶点,P是抛物线上任意一点,H是由P向ξ作垂线的交点. 证明点X=HF×PD的轨迹是一个椭圆.

5. 设F是抛物线的焦点,过抛物线上点A,B的切线交于C, 证明：ΔCAF与ΔBCF相似.由此可得已知抛物线的焦点及它的一条切线及切点作抛物线的其它切线切点的方法.

6. 设抛物线上弦PQ垂直于P处切线,T是P,Q处切线的交点,F是焦点, 过P垂直于PF的直线交TF于C. 证明:TF=FC,CQ⊥TC.

7. 设椭圆的直径AB端点处切线与椭圆上点P的切线交于C,D;E是CF1,DF2的交点,F1,F2是焦点. 试证,ΔCPF1与ΔF2PD,ΔCED相似, ∠CED=∠CPF1是定角(与直径AB的选取无关).

8. 设AA′是椭圆的长轴,F1,F2是焦点,P是椭圆上任意一点,F1Y,F2Y′垂直于P处切线,Y,Y′是垂足. 证明:X=AY×A′Y′的轨迹是一个椭圆.

9. 设椭圆上点P与焦点F1,F2的连线交椭圆于另外两点Q,R;Q,R处切线交于T, 证明：PT是∠QPR的平分线, 且PT垂直于P处切线.

10. 设F是抛物线的焦点, 过准线ξ上点D作抛物线的切线,切点分别是A,B. 证明：DA,DB分别是DF与ξ成两角的平分线. 由此可以得到已知抛物线的焦点准线作抛物线上点与切线的方法.

11. 设F,ξ是圆锥曲线的一对焦点准线,T是曲线上点P,Q处切线的交点, 这两条切线分别交准线于E,S. 证明：∠EFT=∠TFS.

12. 设椭圆上点P的切线与对称轴F1F2交于T,PF1,PF2交椭圆于Q,R,QR交F1F2于S,F1,F2是焦点. 试证:SF1=F2T.

[参 考 文 献]

[1] Busemann H, Kelly P。 射影几何与射影度量[M]. 周纪安,等译.天津：天津师大出版社, 1985.

[2] 周建伟, 高等几何[M], 北京: 高等教育出版社, 2003.