两类特殊图的逆符号边控制数

红 霞, 冯 伟, 徐春雷, 吉日木图

(1.内蒙古民族大学数学学院,内蒙古通辽市028043； 2.内蒙古民族大学计算机科学与技术学院,内蒙古通辽市028043)

1 引 言

本文所指定的图均为无向简单图,文中未说明的符号和术语同文献[1].

设G=(V,E)是一个图,其顶点集V=V(G)和边集E=E(G).对任意u∈V(G),则NG(u)为u点在G中的邻域,NG[u]=NG(u)∪u为u点在G中的闭邻域,δ=δ(G)和Δ=Δ(G)分别为图G的最小度和最大度. 对一个图G,若e=uv∈E(G),用NG(e)表示G中与e相邻边的集合,称为e的边邻域,NG[e]=NG(e)∪{e}为e的闭邻域,用dG(e)表示图G的边e的度.在不混淆的情况下,有时NG(e),NG[e],dG(e)分别简单记为N(e),N[e],d(e).如果d(v)是奇(偶)数,则称v是图G的一个奇(偶)度点.类似的,如果d(e)是奇(偶)数,则称e是图G的一个奇(偶)度边且d(e)=d(u)+d(v)-2.我们定义Eo=e∈E(G)d(e)是奇数,Ee=e∈E(G)d(e)是偶数.

2 基本概念

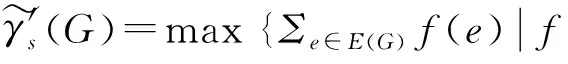
引理2设f为图G的一个逆符号边控制函数且e∈E(G).如果e∈Eo,则Σe′∈N[e]f(e′)≤0.如果e∈Ee,则Σe′∈N[e]f(e′)≤1.

引理3轮图的逆符号边控制数均为偶数.

引理4扇图的逆符号边控制数均为奇数.

近年来,图的控制理论的研究越来越广泛,各种控制概念相继产生,图的符号控制由Dunbar等人于1995年首先提出[2],国内外许多图论工作者对图的符号控制进行了研究,研究成果不断丰富[3-8]. 徐保根于2001年定义了图的符号边控制[6].黄中升于2010年把图的符号边控制引申为图的逆符号边控制[8],并得到了一般图的逆符号边控制数的几个上界.本文给出了所有轮图和扇图的逆符号边控制数.

设x为实数，用

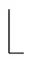
x

e和

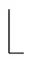
x

o分别表示不超过x的最大偶数和最大奇数.用Wn+1=Cn+K1表示n+1阶轮图(即为K1邻接Cn的每一个顶点而成的图).用Fn+1=Pn+K1表示n+1阶扇图(即为K1邻接Pn的每一个顶点而成的图). 设G=(V,E)是一个图,是一个实数集,对于实值函数f:E→和一个非空子集S⊆E(G),令f(S)=Σe∈Sf(e),并将f(E)称为函数f的权重.下文中,为简单起见,我们称适合f(e)=+1的边为+1边,称适合f(e)=-1的边为-1边,并将f(N[e])记为f[e],记f(G)=f(E(G)).

3 主要结论

定理1对任意正整数n(n≥3)，有

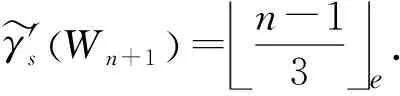
γ'sWn+1 =n-13e.

Σe∈E(Cn)Σe′∈N[e]f(e′)≤n, 即 3f(Cn)+2f(K1.n)≤n.

γ'sWn+1 ≤n-13e.

情况1 当n为奇数时，f(K1.n)总为奇数.显然f(K1.n)≤3(否则任取e∈E(K1.n)有Σe′∈N[e]fe′≥3,矛盾).

情况1.3 当f(K1.n)≤-1时,若n=6k+1,则

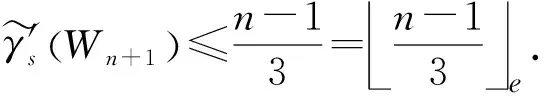
γ'sWn+1 ≤n-13=n-13e .

γ'sWn+1 ≤n-13=n-13e+23.

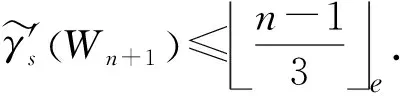
γ'sWn+1 ≤n-13e.

γ'sWn+1 ≤n-13=n-13e+43.

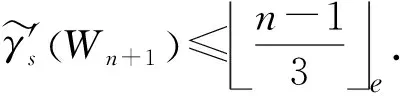
γ'sWn+1 ≤n-13e.

情况2 当n为偶数时，f(K1.n)总为偶数且f(K1.n)≤2.

情况2.3 当f(K1.n)≤-2时,若n=6k+2,则

γ'sWn+1 ≤n-23=n-13e

γ'sWn+1 ≤n-23=n-13e+23 .

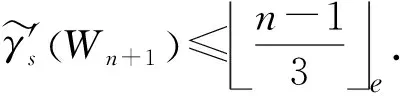
γ'sWn+1 ≤n-13e.

γ'sWn+1 ≤n-23=n-13e+43.

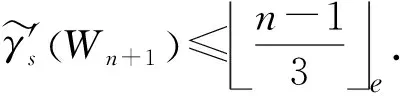
γ'sWn+1 ≤n-13e.

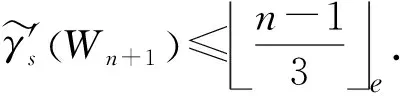
γ'sWn+1 ≤n-13e.

接下来我们证明

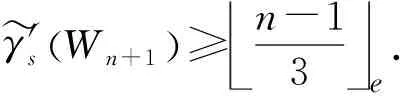
γ'sWn+1 ≥n-13e.

下面仅需定义Wn+1的一个逆符号边控制函数f使得fWn+1=

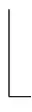
e.

令Wn+1的中心点为v0,即V(K1)=v0,Cn上的顶点依次记为v1,v2,…,vn.显然有

E(Wn+1)=v0vi1≤i≤n∪vjvj+11≤j≤n-1∪vnv1,E(Wn+1)=2n.

(1)当n为奇数时，定义一个函数f：

其下标对n取模

(2) 当n为偶数时，定义一个函数f：

γ'sWn+1 ≥fWn+1 =n-13e,

其下标对n取模.容易验证 故有

γ'sWn+1 =n-13e.

定理2对任意正整数n(n≥3)，有

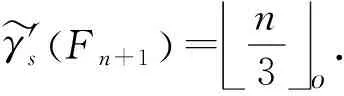
γ'sFn+1 =n3o.

证令扇图Fn+1的扇心为v0,即V(K1)=v0,Pn上的顶点依次记为v1,v2,…,vn.显然有

EFn+1=v0vi1≤i≤n∪{vjvj+11≤j≤n-1}，E(Fn+1=2n-1.

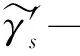
3fPn+2fK1.n-fv1v2-fvn-1vn-fv0v1-fv0vn≤n-1.

下面首先证明

γ'sFn+1 ≤n3o.

情况1 当n为奇数时f(K1.n)总为奇数且f(K1.n)≤1.

情况1.1 当f(K1.n)=1时,f(Pn)≤0,故

fPn ≤22n-1 3-n+1.

情况1.2 当f(K1.n)=-1时，若n≡1(mod 3)，则故

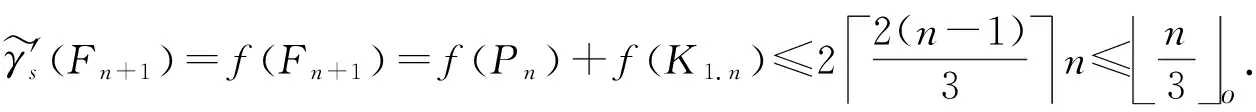
γ'sFn+1 =fFn+1 =fPn +fK1.n ≤22(n-1)3n≤n3o.

fPn ≤22(n-1)3-n+1,

当n≡2(mod 3)时,故

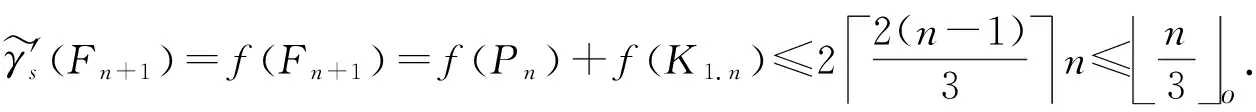
γ'sFn+1 =fFn+1 =fPn +fK1.n ≤22(n-1)3n≤n3o.

fPn ≤22(n-1)3-n+1,

当n≡0(mod 3)时,故

γ'sFn+1 =fFn+1 =fPn +fK1.n ≤22(n-1)3n≤n3o.

情况1.3 当f(K1.n)≤-3时,若n=6k+1,则

γ'sFn+1 ≤n+3+fK1.n 3=n3o+43.

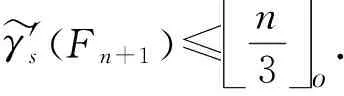
γ'sFn+1 ≤n3o.

由引理4知，若n=6k+3,则

γ'sFn+1 ≤n+3+fK1.n 3=n3o.

若n=6k+5,则

γ'sFn+1 ≤n+3+fK1.n 3=n3o+23.

由引理4知，

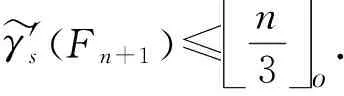
γ'sFn+1 ≤n3o.

情况2 当n为偶数时，f(K1.n)总为偶数且f(K1.n)≤2.

情况2.1 当f(K1.n)=2时,f(Pn)=-(n-1),故

fPn ≤24n-16-n+1.

情况2.3 当f(K1.n)=-2时，若n≡0,1(mod 3),则故

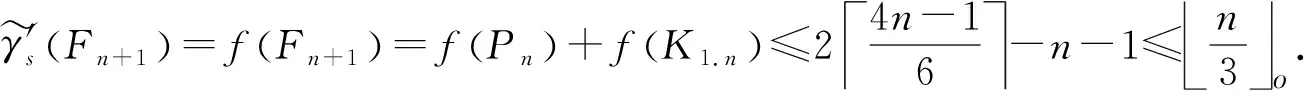
γ'sFn+1 =fFn+1 =fPn +fK1.n ≤24n-16-n-1≤n3o.

fPn ≤24n-16-n+1.

当n≡2(mod 3)时,故

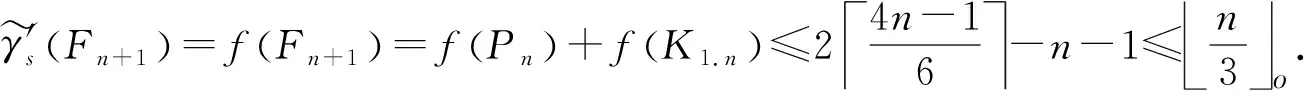
γ'sFn+1 =fFn+1 =fPn +fK1.n ≤24n-16-n-1≤n3o.

γ'sFn+1 ≤n+3+fK1.n 3=n3o+43.

γ'sFn+1 ≤n3o.

γ'sFn+1 ≤n+3+fK1.n 3=n3o.

γ'sFn+1 ≤n+3+fK1.n 3=n3o+23.

γ'sFn+1 ≤n3o.

情况2.4 当f(K1.n)≤-4时,若n=6k+2，则由引理4知若n=6k+4,则若n=6k+6,则由引理4知综合以上两种情况有

γ'sFn+1 ≤n3o.

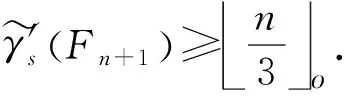
γ'sFn+1 ≥n3o.

接下来证明下面仅需定义f使得

fFn+1 ≤n3o.

(1)当n为偶数时，若n≡0,1(mod 3)，定义一个函数f：

若n≡2(mod 3)，定义一个函数f：

(2)当n为奇数时，若n≡1,2(mod 3)，定义一个函数f：

若n≡0(mod 3)且n≡9(mod 12)，定义一个函数f：

f(e)=-1,当e=v0vn2',(-1)i+1,当e=v0vi或e=v0vn-i+1,1≤i≤n-12,+1,当e=vjvj+1或e=vn-jvn-j+1,j≡0,1(mod 3),1≤j≤n-12,-1,当e=vjvj+1或e=vn-jvn-j+1,j≡2(mod 3),1≤j≤n-12..

若n≡0(mod 3)且n≡3(mod 12)，定义一个函数f：

f(e)=+1,当e=v0vn2,(-1)i+1,当e=v0vi或e=v0vn-i+1,1≤i≤4,(-1)i,当e=v0vi或e=v0vn-i+1,5≤i≤n2,+1,当e=vjvj+1或e=vn-jvn-j+1,j=1,3,4,-1,当e=vjvj+1或e=vn-jvn-j+1,j=2,+1,当e=vjvj+1,j=4+k,k≡0,1(mod 3),-1,当e=vjvj+1,j=4+k,k≡2(mod 3). k=1,2,…,n-9

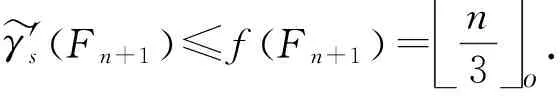
γ'sFn+1 ≤fFn+1 =n3o.

容易验证故有

γ'sFn+1 =n3o.

[参 考 文 献]

[1] Bondy J A and Murty U S R.Graph theory with applications [M]. London and Elsevier: Macmillan, 1976.

[2] Dnbar J. Hedetniemi S,.Henning A, Slater J. Signed domination in graphs[C]. New York: Wiley. Graph Theory, Combinatorics and Applications. 1995.

[3] Hattingh J H, Ungerer E, Henning M A. Partial signed domination in graphs[J]. Ars Combinatoria, 1998,48:33-42.

[4] Zhang Z, Xu B, Li Y, Liu L. A note on the lower bounds of signed domination number of a graph[J]. Discrete Mathematics, 1999,195(1):295-298.

[5] Zelinka B. Signed total domination number of a graph[J]. Czechoslovak Mathematicical Journal, 2001,51(2): 225-229.

[6] Xu Baogen . On signed edge domination numbers of graphs[J]. Discrete Math., 2001,239(1-3):179-189.

[7] Xu Baogen. On signed edge domination numbers of graphs[J].Discrete Math, 2005,294(3):311-316.

[8] Huang Zhongsheng , Xing Huaming Xing, Zhao Yanbing. The upper bounds of inverse signed edge domination numbers of graph[J]. ActaMathematicaeApplicataeSinica, 2010,33(5):840-846.