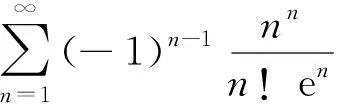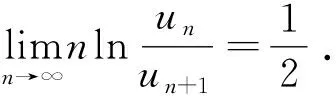交错级数收敛性判别法
房庆祥, 刘雪山, 杨伟能, 张 媛
(1.中国计量学院理学院, 浙江杭州310018; 2.山东省嘉祥县职业中专,山东济宁272400)
1 引 言
对于交错级数的审敛准则,一般高等数学教材[1]上仅介绍莱布尼茨判别法. 对于很多交错级数,应用莱布尼茨定理判别散敛性计算繁琐. 近几年来,很多学者对交错级数的审敛准则进行了深入研究. 2006年,杨万必[2]提出关于判定交错级数收敛性的两个结论. 2010年,刘志高[3]研究了交错级数的对数判别法. 此外,文献[4-7]也提出一些新的交错级数判别法及应用实例. 这些研究工作对判别交错级数的收敛性提供了新的依据. 本文进一步研究交错级数收敛性判别法,提出三个与正项级数的比值判别法和根式判别法类似的收敛性判据,并举例说明它们的应用.
2 交错级数收敛性判据
定理1对于交错级数
(1)
如果存在常数λ,μ,p,l1,l2和数列{θn},满足λ>0,0 (2) 则 (i) 当λ>1时,级数(1)绝对收敛;当λ<1时,级数(1)发散; (ii) 当λ=1时,若μ>0,则级数(1)收敛;若μ≤0,则级数(1)发散. 由于 (3) 当λ=1时,若μ≤0,则由(2)知, 由于 (4) 所以 由定理1,可得如下推论: 推论1对于交错级数(1),如果存在常数λ,μ,p满足λ>0,0 (5) 则 (i) 当λ>1时,级数(1)收敛;当λ<1时级数(1)发散; (ii) 当λ=1时,若μ>0,则级数(1)收敛;若μ≤0,则级数(1)发散. 定理2对于交错级数(1),如果存在常数λ,μ,p,θ,m,λ>0,0 (6) 则 (i) 当λ>1时,级数(1)发散;当λ<1时,级数(1)绝对收敛; (ii) 当λ=1时,若μ≥0,则级数(1)发散;若μ<0,则级数(1)收敛. 证(i) 当λ>1时,由(6)知n充分大时, (7) (ii)当λ=1时,若μ>0,由(6)知 因此,交错级数(1)发散. 若μ=0,由(6)知 因此,交错级数(1)发散. 若μ<0,令 (8) 则 (9) 再令 (10) 和 (11) 则 (12) 且当x→+∞时,g(x)和h(x)同号. 又因为 (13) 所以当x→+∞时,h(x)<0. 由(12)知f′(x)<0. 因此,当n充分大时,{un}单调递减. 由于μ<0,故 根据莱布尼茨判别法知交错级数(1)收敛. 由定理2,可得如下推论: 推论2对于交错级数(1),如果存在常数λ,μ,p,使得0 (14) 则 (i) 当λ>1时级数(1)发散;当λ>1时级数(1)收敛; (ii) 当λ=1时,若μ≥0,则级数(1)发散;若μ<0,则级数(1)收敛. 定理3的证明要用到下面的引理. 引理1(拉贝对数判别法)[8]对于正项级数∑un,若 则 (i) 当l>1时,级数∑un收敛; (ii) 当l<1时,级数∑un发散. 定理3对于交错级数(1),如果存在常数p,l,使得0 (15) 则 (i) 当l>0时,级数(1)收敛. 特别地当p=1且l>1时,级数(1)绝对收敛;当p=1且0 (ii) 当l<0时,级数(1)发散; (iii) 当l=0时,级数(1)有可能收敛,也有可能发散. 从而 即 于是,对于任意正整数m>N1,有 即 当p=1时,由引理1知,若l>1,则级数(1)绝对收敛;若0 例1判断级数 的敛散性(p>0). 因为 [参 考 文 献] [1] 华东师范大学数学系. 数学分析[M]. 北京: 高等教育出版社, 2011. [2] 杨万必. 关于交错级数的审敛准则的改进和推广[J]. 大学数学,2006, 22(2): 138-141. [3] 刘志高. 交错级数的对数判别法[J]. 大学数学,2010,26(2):194-196. [4] 刘晓玲, 张艳霞. 交错级数收敛性的一个判别法[J]. 高等数学研究,2007,10(3): 51-53. [5] 林让起. 交错级数收敛性的两个补充判别法[J]. 红河学院学报,2008,6(2):44-46. [6] 蔡敏, 龚水法. 交错级数收敛的几个结果及其应用[J]. 高等数学研究,2009,12(3): 29-31. [7] 张建军, 宋业新. 关于交错级数收敛性判定的讨论[J]. 高等数学研究,2009,12(3): 38-40. [8] 姬小龙,王锐利. 正项级数的Raabe对数判别法[J]. 高等数学研究,2007 ,10 (3) : 7-9.






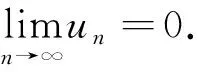
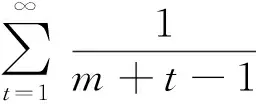
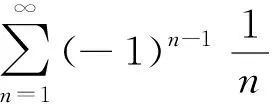

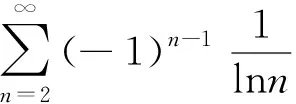
3 判别法的应用