闭连续函数的数列逆保持性

葛 洵， 葛恒武

(苏州大学数学科学学院,江苏苏州215006)

在文[1,2,3] 中, 我们有下述熟知的结论.

命题1设D⊂R,f(x) 是D上连续函数. 如果{xn} 是D中收敛数列, 则 {f(xn)}是f(D)中收敛数列.

作为上述命题的进一步讨论, 一个有趣的问题就是: 命题1是否可逆. 更精确地, 我们有下述问题.

问题1设D⊂R,f(x)是D上的连续函数, 考虑下述性质.

A 对于f(D) 中任一收敛数列 {yn}, 存在D中收敛数列{xn}, 使得{f(xn)}={yn}.

B 对于f(D)中任一收敛数列{yn}, 存在D中收敛数列{xn}, 使得{f(xn)} 是{yn}的子数列.

(i)f(x) 是否具有性质A?

(ii) 更弱一些,f(x) 是否具有性质B?

下面我们首先给出一个例子来说明问题1(i), (ii)的回答都是否定的.

例1设D={0}∪. 定义D上函数f(x)为

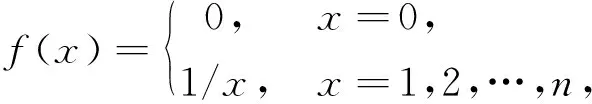
则f(x)是D上的连续函数, 且性质A,B均不成立.

(i) 首先证明f(x)是D上的连续函数.因为D中每一点都是孤立点，而任一函数在孤立点处总是连续的, 所以f(x)是D上的连续函数.

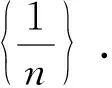
现在我们感兴趣于何种连续映射具有收敛数列的某种逆保持性. 考虑到"闭"与"收敛"的密切联系. 讨论闭连续映射是很自然的. 下述引理是已知的, 见[4, 定理 1.4.13].

引理1设D⊂,f(x) 是D上连续函数, 则f(x) 是闭函数当且仅当对于每一y∈f(D)及任一D中包含f-1(y) 的开子集U, 存在f(D) 中包含y的开子集V, 使得f-1(V)⊂U.

下面给出的例子说明D对于闭连续函数, 性质A不成立.

例2设

定义D上的函数f(x)为

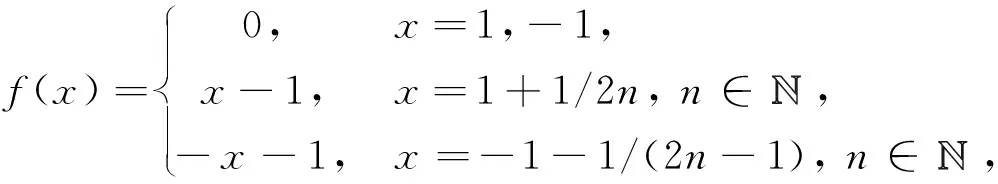
则f(x)是D上的闭连续函数, 但不具有问题1的性质A.

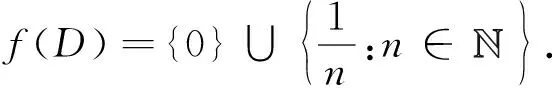
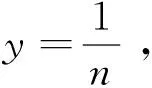
由引理1,f(x)是D上的闭函数.

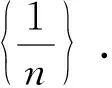
现在我们给出本文的主要定理.

定理1设D⊂.如果f(x)是D上闭连续函数, 则f(x)具有性质B.

证设f(x)是D上的闭连续函数, 任给{yn}为f(D)中收敛于y的数列.

(i) 如果存在无限个n∈, 使得yn=y.这样存在{yn} 的一个子数列{ynk},使得任给k∈,ynk=y. 取x∈f-1(y), 对每一k∈, 令xk=x, 则{xk} 是D中收敛数列, 且{f(xk)}={ynk} 是{yn} 的子数列.

(ii) 如果仅存在有限个n∈, 使得yn=y.不妨设任给n∈,yn≠y，令F={yn:n∈}, 则F不是f(D)中的闭子集. 因为f(x)是闭函数, 所以f-1(F) 不是D中闭子集, 从而存在f-1(F) 在D中的聚点x∉f-1(F). 对每一k∈, 令Fk={yn:n>k}. 下面首先证明, 任给D中包含x的开子集U, 有

U∩f-1(Fk)≠∅.

令Ek={yn:n≤k}, 则f-1(F)=f-1(Fk)∪f-1(Ek). 因为Ek是f(D)中的有限集, 所以Ek是f(D) 中闭子集. 注意到f(x)是连续函数, 且对于连续函数, 值域中闭子集的逆象是定义域中闭子集, 所以f-1(Ek)是D中闭子集且x∉f-1(Ek)⊂f-1(F). 这样对于D中包含x的开子集U,U-f-1(Ek) 仍然是D中包含x的开子集, 所以U-f-1(Ek)∩f-1(F)≠∅.由此得到

U∩f-1(Fk)⊃U∩(f-1(F)-f-1(Ek))=(U-f-1(Ek))∩f-1(F)≠∅.

现在利用归纳法构造收敛于x的数列{xk}. 对每一k∈, 令则Uk是D中包含x的开子集. 因为U1∩f-1(F1)≠∅, 所以存在n1∈, 使得U1∩f-1(yn1)≠∅. 取x1∈U1∩f-1(yn1). 假设已经得到x1,x2,…,xk, 使得对于每一i=1,2,…,k,xi∈Ui∩f-1(yni), 且n1nk,使得Uk+1∩f-1(Fnk+1)≠∅. 取xk+1∈Uk+1∩f-1(Fnk+1). 这样由归纳法, 得到了一个数列{xk}. 显然对每一k∈,f(xk)=ynk, 所以{f(xk)}={ynk}是{yn}的子数列. 此外由于每一xk∈Uk以及由Uk的构造, 容易看出数列{xk}收敛于x.

综上, 我们证明了f(x) 具有性质B.

由定理1的证明可知闭连续映射具有收敛数列性质B的逆保持性. 然而, 我们不知道何种连续映射具有收敛数列性质A的逆保持性. 这仍然是一个值得研究的后续课题.

[参 考 文 献]

[1] 菲赫金哥尔茨.微积分学教程第一卷第一分册[M].北京: 人民教育出版社,1959.

[2] 华东师范大学数学系.数学分析(上册)[M].3版.北京: 高等教育出版社, 2001.

[3] 同济大学数学系.高等数学(上册)[M].6版.北京: 高等教育出版社, 2007.

[4] Engelking R. General topology[M]. Berlin: Heldermann,1989.