分析一道线性代数例题的解法

李志明， 李宏伟

(中国地质大学数理学院，湖北武汉430074)

线性代数是大学的一门基础课程，该课程内容抽象，理论性强，在教学中存在许多难点．国内外线性代数教材种类繁多，各具特色和优点．其中同济大学数学系编、高等教育出版社出版的《工程线性代数》是一本很有代表性的教材. 该教材目前已是第五版，历经数次修编，在结构体系、内容阐述等方面具有主线明确、逻辑清晰、过渡自然、易教易学等特点，因而在全国高校使用广泛，影响深远．

该教材的第123页有如下一道例题，在教材中是第五章的例11．

教材中的解答如下．

得λ1=-1，λ2=λ3=1．

对应单根λ1=-1，可求得线性无关的特征向量恰有1个，故矩阵A可对角化的充分必要条件是对应重根λ2=λ3=1，有2个线性无关的特征向量，即方程(A-E)x=0有2个线性无关的解，亦即系数矩阵A-E的秩R(A-E)x=1．

由

要R(A-E)x=1，得x+1=0，即x=-1．因此，当x=-1时，矩阵A能对角化．

此解法中“矩阵A可对角化的充分必要条件是对应重根λ2=λ3=1，有2个线性无关的特征向量”这一理论在该教材的内容体系中欠周密．

关于矩阵对角化问题的研究，该教材分别在第120页和第123页给出了如下两条定理并予以证明．下面的定理1、定理2分别是教材中第五章的定理2、定理4．

定理1设λ1，λ2，…，λm是方阵A的m个特征值，p1，p2，…，pm是依次与之对应的特征向量. 如果λ1，λ2，…，λm各不相等，则p1，p2，…，pm线性无关．

定理2n阶矩阵A与对角矩阵相似(即A能对角化)的充分必要条件是A有n个线性无关的特征向量．

例1中，对应重根λ2=λ3=1，假设矩阵A有2个线性无关的特征向量p2，p3，同时设对应单根λ1=-1，A的特征向量为p1，那么p1，p2，p3的线性相关性如何呢？这个根据定理1并不能直接得出，因为定理1只是描述了对于每个特征值仅有单个特征向量的情形．由定理1可以得到的是，p1与p2线性无关，p1与p3线性无关．

例1的解法可完善如下．

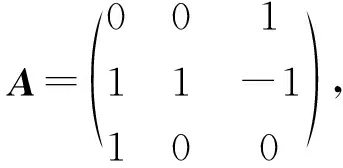
λ1=-1时，解方程(A+E)x=0．由

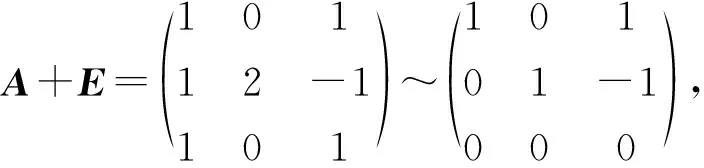
得基础解系p1=(-1,1,1,)T，p1是对应于λ1=-1的特征向量．

λ2=λ3=1时，解方程(A-E)x=0．由

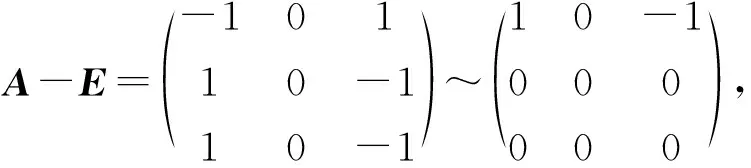
得基础解系p2=(0,1,0)T，p3=(1,0,1)T，p2，p3是对应于λ2=λ3=1的特征向量．而

所以p1，p2，p3线性无关，从而矩阵A有3个线性无关的特征向量，故A能对角化．

也即是在求解中加入了充分性的验证．

实际上，定理1可推广为下面的定理3．

定理3设λ1，λ2，…，λm是方阵A的不同特征值，而pi1，pi2，…，piri是对应于特征值λi的线性无关的特征向量 (i=1,2,…,m)，那么向量组p11，p12，…，p1r1，p21，p22，…，p2r2，…，pm1，pm2，…，pmrm线性无关．

此定理在不少代数教材中有陈述和证明，如文献[2]．

若基于此定理，则教材中的解法是完全正确的．

因为本文讨论的教材没有介绍这一定理，所以例1的解法还是周全严谨为宜．

[参 考 文 献]

[1] 同济大学数学系．工程线性代数[M]．5版.北京：高等教育出版社，2013：117-124．

[2] 邱森．高等代数[M]．2版.武汉：武汉大学出版社，2012：210-216．