随机变量积的分布函数及其应用

刘 洋， 何 璐， 孙丽英， 许贵桥

(天津师范大学数学与应用数学系，天津300387)

1 引 言

统计推断是根据带随机性的观测数据(样本)以及问题的条件和假定(模型)而对未知事物作出的以概率形式表述的推断.统计推断的应用已经遍及几乎所有科学技术领域，在质量管理活动中应用尤其普遍.因此，如何提高推断的准确性，是国内外研究的一个热点问题.随机变量的分布函数是统计推断的理论基础，现在各种推断方法中均假定随机变量为连续型分布，而实际问题有许多都是连续型随机变量与离散型随机变量的积，如单个电器的寿命为指数分布(连续型)，而工厂随机生产的电器数量为泊松分布(离散型)，提供的总服务时间实际为连续型分布与离散型分布的积，把它用连续型随机变量来处理是失真的，因此推断所得结果的准确性也是有问题的.注意到目前为止,文献[1，2]得到了利用Lebesgue-Stieltjes积分给出的一般随机变量的和的分布函数，而文献[3]给出了一般随机变量的差的分布函数，但有关随机变量积的分布函数计算公式仅限于两个随机变量均为离散型或均为连续型，因此我们将利用Lebesgue-Stieltjes积分给出一般随机变量的积的分布函数计算公式，并由此公式处理一些实际问题.下面具体叙述问题.

设ξ是一个随机变量，x是任意实数，称函数

F(x)=P{-∞<ξ≤x}

为ξ的分布函数，其满足性质：

1.F(x)在(-∞,+∞)上单调不减；

2.F(x)任意点x处皆右连续；

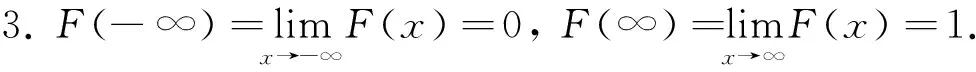
(1)

若ξ，η均为连续型随机变量且互相独立，则容易得出其积的分布密度函数；若ξ，η均为离散型随机变量且相互独立，则容易得出其积的分布列.但当ξ，η分别是连续型随机变量和离散型随机变量时，其积的分布问题尚未见到导论.本文将利用Lebesgue-Stieltjes积分给出相应的分布函数，并用实例说明其应用.

2 随机变量积的分布函数

定理1设ξ是一个连续型随机变量，分布函数为F(x)，η是一个随机变量，分布函数为G(x).若ξ，η是互相独立的，则随机变量ζ=ξη的分布函数为

其中G(x-)表示函数G(x)于x处的左极限，而

证由ξ，η的独立性及F(x) ，G(x)的定义可知在二维随机变量(ξ,η)中，事件a<ξ≤b,c<η≤d的概率为

P(a<ξ≤b,c<η≤d)=(F(b)-F(a))(G(d)-G(c)).

(2)

由(2)及二重积分的定义可知，对任意二维空间的Lebesgue可测集E,有

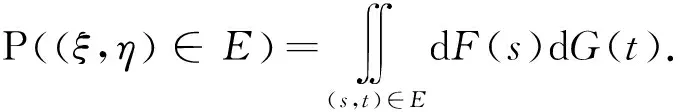
(3)

由(3)可得对任意x∈(-∞,∞)

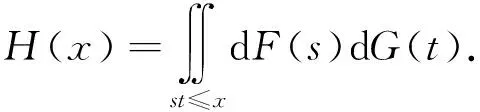
(4)

由Fubini定理可知此二重积分可先化为关于s再关于t的二次积分，即

(5)

其中

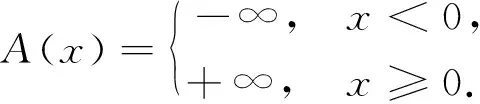
(6)

由分布函数的定义及(1)可得

(7)

由F(x)的连续性及(1)可计算得

(8)

由Lebesgue-Stieltjes积分的定义及(1)可得

(9)

由(5)-(9)可得

注1 若ξ,η均为连续型随机变量且互相独立，其概率密度分别为f(x),g(x)，则

(10)

此时由定理可知ζ=ξη的分布函数为

(11)

由(11)可知ζ=ξη的概率密度为

即定理1是连续型随机变量积的密度函数求积公式的推广.

注2 若η为离散分布，其分布列为

(12)

则由定理可知ζ=ξη的分布函数为

(13)

注3 对任意两个随机变量，定理1不一定成立.例如，若ξ,η分别为取值为1和-1的单点分布，则

(14)

由(14)直接计算可得

(15)

由于其不是右连续的，因此其不等于ζ=ξη的分布函数.

3 随机变量积的相关实例

例1 学校教务处欲建立一办公室为学生提供咨询服务，经调查知道单位时间内的学生平均咨询次数量为λ，每次咨询的平均服务时间为μ，在此情况下办公室至少安排几名工作人员，才能使得学生咨询无须等候的概率不小于0.9？

解由于学生的咨询是随机的，故由概率知识知道每次服务的时间ξ服从均值为μ的指数分布，其分布函数为

(16)

由概率知识知道单位时间内的咨询次数η服从均值为λ的泊松分布，其分布列为

(17)

办公室在单位时间内需要的总咨询为ζ=ξη.因此由(13)，(16)和(17)可得ξ的分布函数为

(18)

由H(x)的严格单调性知方程

的根是唯一的.求出其根A.当工作人员的个数大于A时，才能保证学生咨询无须等候的概率不小于0.9.

例2某养羊牧场每年冬天出售成羊，同时选择种羊供下年用.现已知每只母种羊平均生λ只羊羔，羊群每年秋天的个体食草量的需求服从正态分布N(μ,σ2).牧场每年秋天的蓄草量是稳定的，其值为A.当羊群的总食草量需求超过牧场的蓄草量时，羊群就会由于饥饿大批死亡且引发一系列环境问题.问冬天应如何保留种羊，才能保证羊群安全过秋的概率不小于0.95？

解假设羊群第二年无意外死亡，则若保留n头公种羊与m头母种羊，则由概率知识知第二年秋天羊的数量η的分布列为

(19)

记ξ为正态分布N(μ,σ2)，则其分布函数为

(20)

羊群的总食草量需求为ζ=ξη，因此由(13)，(19)和(20)可得ζ的分布函数为

(21)

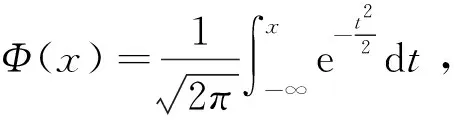
(22)

再令

(23)

当n,m满足(23)式时，才能保证羊群安全过秋的概率不小于0.95.

[参 考 文 献]

[1] 王梓坤.概率论基础及其应用[M].北京：科学出版社.1976.

[2] 杨丰凯.离散型随机变量与连续型随机变量之和的分布[J].吉林师范大学学报(自然科学版).2005，11(4)：95-96.

[3] 田贵辰,高印芝,胡景明.随机变量的差的分布函数的积分表达式[J].大学数学.1998，14(4)：125-127.

[4] 魏宗舒，等.概率论与数理统计教程[M]. 北京：高等教育出版社.1983.

[5] 周民强.实变函数[M].北京：北京大学出版社.1995.