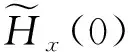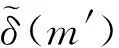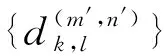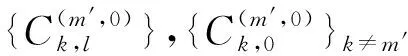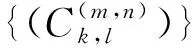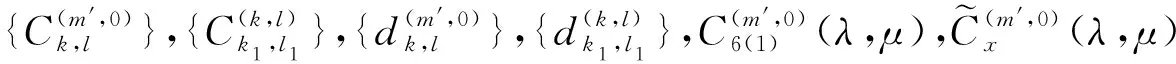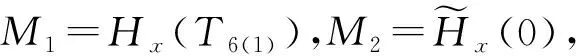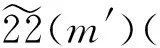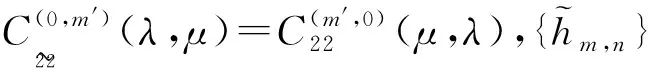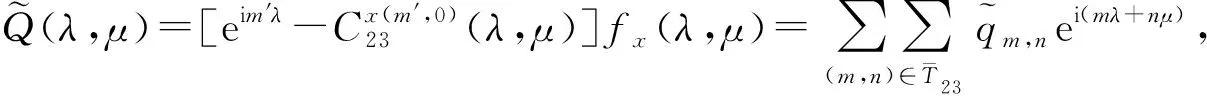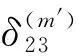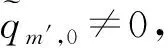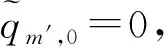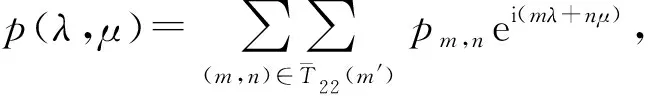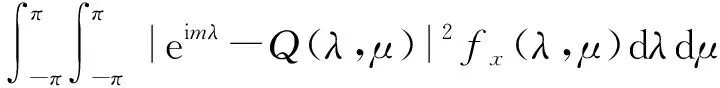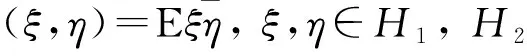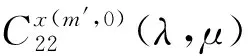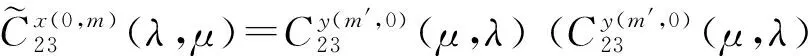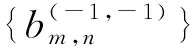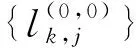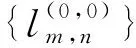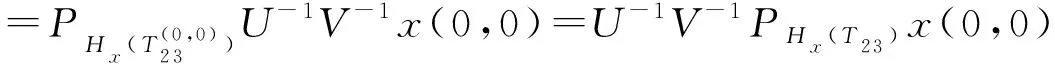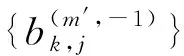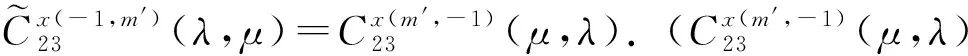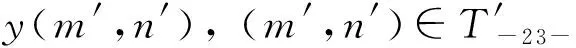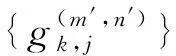具有离散参数齐次随机场的线性预测(XVII)
徐业基
(复旦大学管理学院统计系,上海200433)
设齐次随机场{x(m,n)}是含有两个取整数值m,n的齐次随机场,Ex(m,n)=0,它的线性预测问题的一般提法是:设T及T′是平面上格子点的两个集合,当(m,n)∈T时,{x(m,n)}值已观察到,而当点(m′,n′)∈T′时,{x(m′,n′)}值未知,现在要以已观察到的值的线性组合及均方意义下的极限去预测未观察到的值{x(m′,n′),(m′,n′)∈T′},使均方误差最小.熟知,其预测值是PHx(T)x(m′,n′),其中P是正交投影算子,Hx(T)是由{x(m,n),(m,n)∈T}所张成的线性闭包.
江泽培[1,2]首先研究了半平面的线性预测理论(即T={(m,n),-∞ 引理1[1,2]设齐次随机场{x(m,n)}的谱函数绝对连续,谱密度为fx(λ,μ),且为垂直正则 dZx(λ,μ)是{x(m,n)}的随机谱测度,则 (1) (2) (3) (4) 若进一步设f(λ,μ)有正的上、下界,则 (5) 引理2[4]设齐次随机场{x(m,n)}的谱函数绝对连续,谱密度fx(λ,μ)有正的上、下界,则预测问题6(1) (即T={(m,n),-∞ (6) (7) (8) {φ(λ)}由下列式决定 (9) (10) 又预测问题6(1)线性预测x(m,n), (n≥1),其预测值为 (11) 引理3[5]设H1是Hilbert空间,H2是H1中的一个子空间,x,y∈H1.若x-y正交于y及H2,则‖x-y‖≤‖x-PH2x‖,且这式等号成立的充分必要条件是y=PH2x. 引理4(Neumann) 设P1,P2及P分别是Hilbert空间M1,M2及δ(M1,M2)的正交投影算子,其中δ(M1,M2)是由M1,M2所张成的线性闭包,则 P1+P2-P2P1,P1+P2-P2P1-P1P2+P1P2P1, P1+P2-P2P1-P1P2+P1P2P1+P2P1P2-P2P1P2P1… 强收敛于P. 定理1设齐次随机场{x(m,n)}的谱函数绝对连续,谱密度fx(λ,μ)有正的上、下界,则预测问题22(m′)(即T={(m,n),m≤0或n≤0}{(m′,0)}(m′>0)T′22(m′))线性预测x(m′,0)的预测值为 (12) 其中 (13) 预测误差为δ22(m′): (13′) 用以上方法可计算P1P2P1,P2P1P2,…,一起代入,即证明定理1. (14) 证作x(m,n)=y(n,m),则x(m,n)仍为齐次随机场,谱函数绝对连续,谱密度fx(λ,μ)=fy(μ,λ),且有正的上、下界,随机谱测度dZx(λ,μ)=dZy(μ,λ),再由定理1知 定理2证毕. 定理3设齐次随机场{y(m,n)}的谱函数绝对连续,谱密度fx(λ,μ)为正,且有界,则预测问题23线性预测x(m′,0)的预测值为 (15) 其中Hx(T23)是由{x(m,n),m≥1,n≥1}所张成的线性闭包,而预测误差为 (16) (17) (18) 证由正交投影的性质知,当(m,n)∈T23时 (19) 再由 得 (20) (21) 结合(20),(21)得 (22) (23) qm,n=pm,nqm′,0(m,n)∈T22(m′), (23′) 则容易验证qm′,0{qm,n}满足关系式 (24) 又记 (25) (26) 则有 事实上,若qm′,0≠0,则 即知E|Q|2<∞.若qm′,0=0,则 关于x(m′,0)-Q与Q及Hx(T23)的正交性可直接由Q的定义来验证. 下面记HQ是(23),(23′),(25)中变动{pm,n}所得的Q全体,对HQ中任意一个元素Q,若qm′,0≠0,则 若qm′,0=0,则由qm′,0的定义得 由此推出 (28) 结合(22)与(28)式,即证得(16). (29) 定理4设齐次随机场{y(m,n)}的谱函数绝对连续,谱密度fy(λ,μ)有正的上、下界,记Zy(λ,μ)是{y(m,n)}的随机谱函数,则预测问题23线性预测y(m′,0) (m′>0)的预测误差为 (30) 其中δ22(m′)是谱密度为fx(λ,μ)的齐次随机场{x(m,n)}的预测问题22(m′)线性预测x(m′,0)的预测误差,由定理1中的(13′)决定. 预测值为 (31) (32) (33) (34) 利用上面的结果及方法,即可证明定理4. 定理5设齐次随机场{x(m,n)}的谱函数绝对连续,谱密度fx(λ,μ)有正的上、下界,则预测问题23线性预测x(0,m′) (m′>0)的预测值为 (35) 结合定理4,证法类似定理2,故证明从略. 今后我们称PHx(T23)x(0,0)为顶一步预测值,PHx(T23)x(m′,0) (m′>0)为右一步预测值,PHx(T23)x(0,m′) (m′>0)为左一步预测值.它们总称为一步预测值.下面我们讨论二步预测问题,即要求得PHx(T23)x(-1,-1) (顶二步预测值),PHx(T23)x(m′,-1) (m′≥0) (右二步预测值),PHx(T23)x(-1,m′) (m′≥0) (左二步预测值).它们总称为二步预测值.我们定义推移算子U-1为U-1x(m,n)=x(m-1,n),V-1为V-1x(m,n)=x(m,n-1). 定理6设齐次随机场{x(m,n)}的谱函数绝对连续,谱密度fx(λ,μ)有正的上、下界,则预测问题23线性预测x(-1,-1)的预测值(预二步预测值)为 (36) (37) 证预测问题23线性预测x(0,0)的预测值为 (38) (39) 再结合(38)得 (40) 故结合(38),(39),(40)及定理4,定理5得 PHx(T23)x(-1,-1) 定理6证毕. 定理7设齐次随机场{x(m,n)}的谱函数绝对连续,谱密度fx(λ,μ)有正的上、下界,则预测问题23线性预测x(m′,-1),m′≥0的预测值(右二步预测值)为 (42) (43) 证明类似于定理6的证明,故从略. 定理8设齐次随机场{x(m,n)}的谱函数绝对连续,谱密度fx(λ,μ)有正的上、下界,则预测问题23线性预测x(-1,m′),m′≥0的预测值(左二步预测值)为 (44) 证法类似于定理2,故从略. 注 由定理6,定理7,定理8,我们求得了预测问题23的二步预测值,从而以此类推,同法可求得任意步预测值. (45) (46) 证作x(m,n)=y(-m,-n),则{x(m,n)}仍为齐次随机场,谱函数绝对连续,谱密度f(λ,μ) =f(-λ,-μ),随机谱测度dZk(λ,μ)=dZy(-λ,-μ), 定理9证毕. [参 考 文 献] [1] CHIANG T P. On linear extrapolation of a discrete homogeneous field[J]. Dokl. Nauk SSSR, 1957, 112: 207-210. [2] 江泽培.平稳随机场的预测理论(I):半平面预测[J].北京大学学报,1989,25(1): 25-50. [3] 徐业基.具有离散参数齐次随机场的线性预测(X)[J].高校应用数学学报A辑,2002,12(1):74-82. [4] 徐业基.具有离散参数齐次随机场的线性预测(XIII)[J].纯粹数学与应用数学,2005,21(2):172-179. [5] 徐业基.具有离散参数齐次随机场的线性预测(II)[J].复旦学报,1983,22(3):307-315. [6] 徐业基.具有离散参数齐次随机场的线性预测与马氏性(III)[J].科学研究月刊,2007,31(7):57-59. [7] 徐业基.具有离散参数齐次随机场的线性预测与马氏性(V)[J].科学研究月刊,2008,45(10):67-72.