基于特征值理论求分式线性递推数列极限
李 颖, 周 敏, 倪谷炎
(国防科学技术大学理学院数学与系统科学系,长沙410073)
1 引 言
分式线性递推数列是高等数学的研究对象之一,它在理论与实际问题中有着广泛的应用.目前求分式线性递推数列的通项表示形式常用的方法有不动点方法[1]、矩阵方法[2]以及换元解法[3].本文将利用系数矩阵的特征值以及映射的不动点对分式线性递推数列敛散性进行研究.
2 基本概念

定义2[5]设X是度量空间,T是X到X中的映射.若x∈X,有Tx=x,则称x为T的不动点.
定义3[6]设方阵A=[aij]n×n∈n×n. 若存在数λ和非零的n维列向量ξ,使得Aξ=λξ,则称λ为A的特征值,向量ξ为A的对应于特征值λ的特征向量.
3 矩阵特征值与映射不动点的关系

(i)λ1≠λ2的充要条件是ξ1≠ξ2;λ1=λ2的充要条件是ξ1=ξ2;
(ii)λ1-d=cξ1,λ2-d=cξ2,cξ2=a-λ1,cξ1=a-λ2.
证系数矩阵A的特征方程为
|λE-A|=λ2-(a+d)λ+(ad-bc)=0.

注1 定理1给出了系数矩阵A的特征值与映射f(x)的不动点之间的关系式.
注2 定理1中系数矩阵的特征值即为文献[3]换元解法中的二阶常系数齐次线性差分方程yn+2-(a+d)yn+1+(ad-bc)yn=0的特征根.
4 判断分式线性递推数列敛散性方法
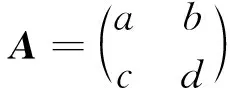

接下来,基于矩阵方法与矩阵理论分析特征值对分式线性递推数列敛散性的影响以及与极限值、不动点之间的关系.基于定理1和定理3可得

当x1=ξ1时,数列{xn}为常数列并收敛于ξ1;当x1=ξ2时,数列{xn}为常数列并收敛于ξ2.


当|λ1|=|λ2|且x1≠ξ1,ξ2时,数列{xn}发散.

证由定理3 可知,若λ1≠λ2,与系数矩阵An对应的分式线性递推数列的通项公式为
整理后可得

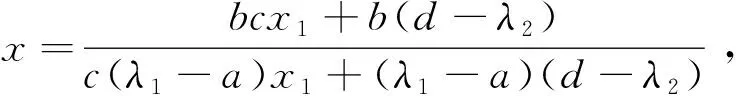

易知数列极限不存在,因此数列{xn}发散.



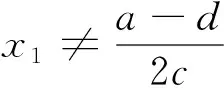
注1 当λ1≠λ2时,数列{xn}的通项公式为
将特征值与不动点的关系式代入整理,可得由不动点、初始值以及系数表示的通项公式如下
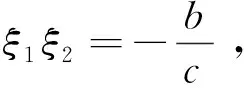
与文献[1]利用不动点方法所得的通项公式一致.

同样利用特征值与不动点的关系式以及cξ2=-b,可得
与文献[1]所得的通项公式一致.




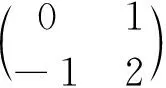
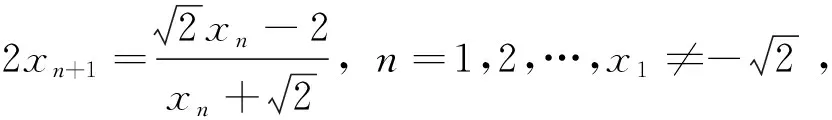

[参 考 文 献]
[1] 郑隆炘. 归纳与递推[M]. 武汉:湖北教育出版社,1984.

[3] 孙胜先,余丙森. 分式线性递推数列极限的换元解法[J]. 高等数学研究,2011,14(4): 72-74.
[4] 石岩. 关于分式递推数列的若干研究[D]. 华南师范大学硕士学位论文,2010.
[5] 张玲. 关于压缩映射原理的某些应用[J]. 科技通报,2011,27(4):474-478.
[6] 冯良贵,戴清平,李超,谢端强. 线性代数与解析几何[M]. 北京: 科学出版社,2008.


