需求依赖销售努力和销售价格的库存模型

李 彤， 李清艳， 杨志林

( 合肥工业大学数学学院，安徽合肥230009)

1 引 言

随着经济的飞速发展，商业竞争的越发激烈，许多企业相继加大销售努力来刺激消费者的需求.根据美国国家统计局提供的数据显示，美国企业的广告费用投入从1990年的1300亿美元增加到2000年的2360亿美元.众多研究者也用数据证明了经过适当的促销手段能增加商业利润.例如文献[1]和[2]对供应商提供临时价格折扣时的销售商的最优库存决策问题进行了研究，并且获得了一些有价值的成果，但其研究均基于如下假设：零售商的需求是固定不变的. [3](第6章)简述了需求只依赖销售努力的情况下销售商的最优库存决策. [4]探讨了考虑努力及价格因素的易逝品供应链协调问题. [5]研究了随机需求是关于价格和广告费用的一般函数的前提下，提出了一个一般的newsboy模型，给出了寻求最优广告费用、销售价格及订货量的分析方法.2007年，何勇、吴清烈和赵林度在需求不确定且与努力水平和零售价格具有相关性的前提下, 建立了弹性数量契约模型, 并重点探讨以下两个主要内容，一是如何确保供应链协作，二是如何确定最优的努力水平、零售价格和订购量.2010年，汪峻萍，周永务，杨剑波[7]提出了同时考虑了需求依赖销售价格和销售努力的决策模型，给出了寻求最优销售努力投入、销售价格及订货量的分析方法.这是在假定随机需求的前提下建立的决策模型，并分析了需求的不确定性对最优销售价格和销售努力的影响.

虽然现有文献已建立了需求依赖价格以及广告费用的模型，但在假设确定性需求的前提下，很少有文献涉及销售价格和销售努力投入同时决策的问题，原因是同时考虑这两个因素难以给出分析解.而实际的市场运作当中同时采用这两种营销手段的商品比比皆是.比如爱国者、金士顿等移动闪存盘，各类品牌服装等.本文则在假定销售商的需求函数同时依赖价格和销售努力的前提下，以最优的销售努力来刺激消费，帮助销售商制定最优的最优订购量，实现利润最大化.最后通过数值实例验证了模型的求解过程并得到相关启示：增加销售努力是非常有必要的.而在增加销售努力的同时，销售量也大大增加了，这对制造商也是非常有利的.

2 记号与假定

本文提出的数学模型所用的记号与假设如下：

记号

(i)Q表示销售商在销售期初的订购量.

(ii)w表示销售商的单位进价，p表示销售商的单位产品的销售价格.

(iii)A表示销售商每次固定的订货费用，h表示销售商单位时间单位产品的库存费用占购买的百分比.

(iv)I表示销售商在每个销售周期所作的销售努力投入.

假定

(i) 假设系统运行在无限周期水平上，不允许缺货，补货率是瞬时的；

(ii)供应商与销售商之间实行“批对批”策略，因此在制造商处不考虑库存费用；

3 模型的建立与分析

根据以上假设，本章的决策问题变为：怎样同时决定销售商的最优销售投入、最优销售价格以及最优订购批量. 下面本章据此建立以下模型.

3.1 增加销售努力

令ATP(p,I,Q)表示销售商在一个周期内的平均总利润函数， 根据上面的记号与假定，平均总利润可表示为

ATP(p,I,Q){销售收入-购买成本-库存成本-订购成本-销售努力投入}

(1)

令

(2)

即

(3)

得

即证明I*为式(2)关于I的最大值.

同时令

(4)

即

(5)

得p*. 而

(6)

式(6)说明p*为式(4)关于p的最大值.

下面证明对于给定的Q,I*和p*可使式(1)取得最大值.

即说明I*和p*是Q的最优函数，把I*和p*代入式(1)后，函数就成为关于Q的一维函数ATP(p*(Q),I*(Q),Q).令ATP1(Q)=ATP(p*(Q),I*(Q),Q)，下面求最有订购批量Q*，以使得ATP1(Q)取得最大值.

首先，由ATP1(Q)的一阶最优性条件得

(7)

将上式进一步化简可得

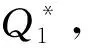
(8)

预分析式(8)的根的情况，我们先研究ATP1(Q)的二阶导数.

(9)

令式(9)为零，即有

(10)

其中D(I,p)=a-bp+αIβ.

3.2 没有增加销售努力

(11)

对p求一阶偏导并令其等于零，

(12)

令ATP(p*(Q),Q)=ATP2(Q)，下面求最优销售价格Q*,以使得ATP2(Q)取得最大值.

由ATP1(Q)关于Q的一阶最优性条件得

(13)

令上式等于零，有

(14)

(15)

3.3 两种情形下利润函数的比较

增加销售努力情形下利润函数为

(16)

没有增加销售努力情形下利润函数为

(17)

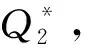
3.4 最优解分析

命题1目标函数1中，当α,β一定时，Q值只与I有关.

证已知需求函数为D(I,p)=a-bp+αIβ,α,b>0,p>a/b, 0<β<1，故有

D′I=αβIβ-1.

由式(3)和式(5)得

b=QD′I=QαβIβ-1，

即Q值只与I有关.

命题2当其它参数已知时，目标函数1的最优值只与α,β有关.

证由命题1得

(18)

由式(5)和式(18)得

(19)

代入式(10)，得

两边同时平方，化简，得

(20)

因此，式(20)中计算所得的I值只与α,β有关.又由式(5)和式(19)知，p,Q只与I值有关，故整个最优目标函数1的值只与参数α,β有关.

3 实例分析

下面结合实例给出最优解的数值分析及关于参数α,β的灵敏度分析.

例1假定销售商所面临的需求函数为D(p)=36000-4000p，每次订购货物所需的固定费用为A=150元，购买单位产品的成本为c=3元，单位产品在单位时间内平均库存持有成本占销售商单位购买成本的百分比为h=0.4.试问销售商如何制定其订购策略以及销售价格？

解首先利用迭代算法2可得最优订购批量Q*=1719(单位)，然后再利用式(12)得出最优销售价格p*=6.04(元)，将所得的Q*和p*代入式(11)可得销售商的最优平均利润为ATP*(p,Q)=33929(元).

例2假定销售商在投入销售努力以后所面临的需求函数为

D(I,p)=a-bp+αIβ,α,b>0,p>a/b,0<β<1，

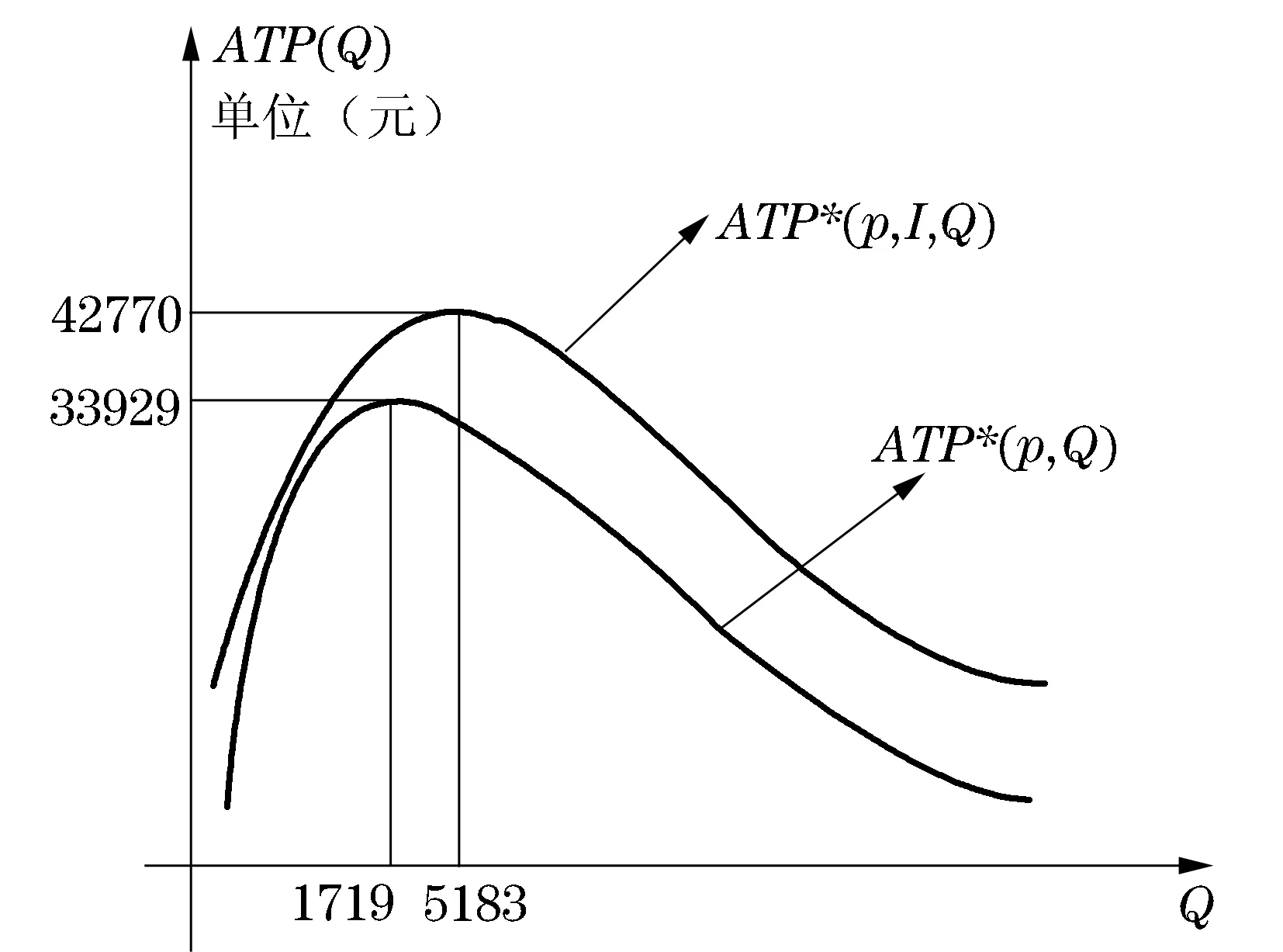
图1 表示目标函数ATP*(p,I,Q)和ATP*(p,Q) 的图像

其他参数与例1相同，即

a=36000,b=4000,c=3,A=150,

h=0.4,α=1000,β=0.2，

试问该销售商又该如何制定其订购策略以及销售价格？

解用上述同样方法得出I*=1040(元),Q*=5183(单位),p*=6.62(元), 代入式(19)可得销售商的最优平均利润为ATP*(p,I,Q)=42770 (元).与例1比较可参照图1 .

由上图很明显可以看出

ATP*(p,I,Q)>ATP*(p,Q).

经过对比即可看出，加入销售努力会给销售商带来较为客观的收益.

例3假定其他条件不变，讨论参数α,β的变化对最优解的影响.

表 1

由表1可以看出，当α=1000，β=0.2时，销售价格，订购量最接近实际.而由图2和图3可以看出，函数ATP*(p,I,Q)随着α的增大而增大，随着β的增加而减小.故综合比较来看，取α=1000，β=0.2比较合适.

图2 表示目标函数ATP*(p,I,Q)关于α的图像 图3 表示目标函数ATP*(p,I,Q)关于β的图像

图 4 表示两个目标函数利润的差值

4 结 论

企业在市场运作过程中通常会使用价格和广告这两个重要手段，本文也证明了在适当增加了销售努力以后企业的平均利润有所增大， 但是由图1和图4可以看出其收益的差距不是太大.

这是因为由于实际运行中，增加销售努力会同时给供应商与销售商带来收益，一般情况下供应商会通过对销售商进行销售补贴来共同分担销售努力投入.本文的进一步的研究方向是，通过制定完善的销售契约来促使供应商与单个甚至多个销售商协调分担销售努力的投入，以此来达到供应链整体的最优利润.

[参 考 文 献]

[1] Arcelus F S, Srinivasan G . Price discounts for extraordinary purchases[J]. Opsearch, 1992. 29(3): 203-215.

[2] Goyal S K, Srinivasan G, Arcelus F J. One time only incentives and inventory poliaies [J]. European Joural of Operational Research, 1991. 54(1):1-6.

[3] 吴广谋，吕周洋. 博弈论基础及其应用[M].南京：东南大学出版社, 2009.

[4] 何勇,吴清烈,赵林度. Quantity flexibility contract with effort and price-dependent demand[J]. Systems Engineering and Electronics，2007, 29(12): 2056-2059.

[5] 周永务，等. 库存控制理论与方法[M].北京：科学出版社，2009.

[6] 闵杰，周永务. 库存水平影响需求变化的供应链协调[J]. Journal of Fudan University，2007. 0427-7104 (2007) 04-0523-09.

[7] 汪峻萍,周永务,杨剑波.需求依赖广告费用和销售价格的newsboy型产品库存模型[J].控制与决策,2010,25(1):89-92.

附录Ⅰ：

算法1

步骤1：输入参数值，并令k=0和Q0=∞.

步骤2：利用式(3)得出I*(Qk)=∞.

步骤3：利用式(5)得出p*(Qk)=∞.

附录Ⅱ：

算法2

步骤1：输入参数值，并令k=0和Q0=∞.

步骤2：利用式(14)得出p*(Qk)=∞.

步骤4：如果|Qk+1-Qk|<ε停止；否则，令k=k+1，转入步骤2.