SPSS在数学建模中的应用实例

周 静

（天津冶金职业技术学院，天津 300400）

在数学建模中，由现实数据建立模型，通常采用的方法是回归分析。回归分析是通过规定因变量和自变量来确定变量之间的因果关系，建立回归模型，然后根据模型参数来评价该模型的拟合情况，并可根据自变量作进一步预测。较之Matlab数学软件中的回归分析功能，SPSS统计软件的优势在于其图形交互式用户界面更易于操作，且数据结果可读性强、容易导出。下面，以某公司生产的牙膏销售量为例，利用SPSS18．0进行回归分析，建立牙膏的销售量与其它因素的回归模型，说明SPSS在解决数学建模中预测问题时更具优越性。

一、数据来源

某大型牙膏制造企业为了更好地拓展产品市场，有效地管理库存，公司董事会要求销售部门根据市场调查，找出公司生产的牙膏销售量与销售价格、广告投入等之间的关系，从而预测出在不同价格和广告费用下的销售量。为此销售部的研究人员收集了过去30个销售周期（每个销售周期为4周）公司生产的牙膏的销售量、销售价格、投入的广告费用，以及其他厂家生产同类牙膏市场的平均销售价格。

二、数据分析

因消费者在购买牙膏时，更关心的是不同品牌之间的价格差，所以在研究各个因素对销售量的影响时，采用价格差代替公司的销售价格和其他厂家平均价格作为影响因素之一。因此，将价格差和广告费用作为自变量，牙膏的销售量作为因变量，采用SPSS18．0中文版进行数据分析。

（一）绘制散点图

打开数据文件窗口的对话框，在菜单栏依次单击“图形”→“旧对话框”→“散点／点状”，选择“简单分布”，并分别将广告费用和价格差作为自变量选入X轴，销售量作为因变量选入Y轴，绘制散点图。

图1 广告费用与销售量的散点图

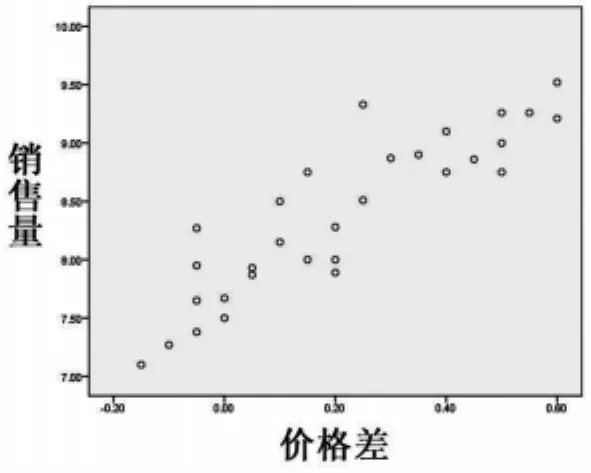
图2 价格差与销售量的散点图

（二）曲线估计

从散点图来看，价格差与销售量呈现较明显的线性趋势，而广告费用和销售量呈现较明显的曲线趋势，但要判定两个变量更适合于哪个模型，则需要进行曲线估计。在菜单栏依次单击“分析”→“回归”→“曲线估计”，分别将广告费用和价格差选入自变量，销售量选入因变量，在模型选项组勾选“线性曲线”、“二次项曲线”和“立方曲线”三种曲线回归模型。

表1 广告费用与销售量曲线估计的模型摘要

由表1可以看出，三个曲线估计的回归模型中，二次项曲线模型与立方曲线模型的拟合度显著优于线性模型，其中拟合度最好的是二次项曲线模型，其R2值为0．838，并且从F值来看，二次项曲线模型比立方曲线模型拟合的更为显著。因此，选择二次项曲线模型最为理想，即y＝β0＋β1x1＋β2x12＋ε，其中x1为广告费用，y为销售量，ε为随机误差，βi为回归系数。

表2 价格差与销售量曲线估计的模型摘要

由表2可以看出，三个模型的拟合度基本相同，其中拟合度最好的是立方曲线模型，其次是二次项曲线模型，但立方曲线模型的参数比另外两种模型的参数多，更为复杂。若从F值来看，线性模型拟合的最为显著。但以上的结果还不足以作出判断，还需要对各模型系数作显著性检验。重复上述操作，并且在曲线估计对话框勾选“显示ANOVE表格”。

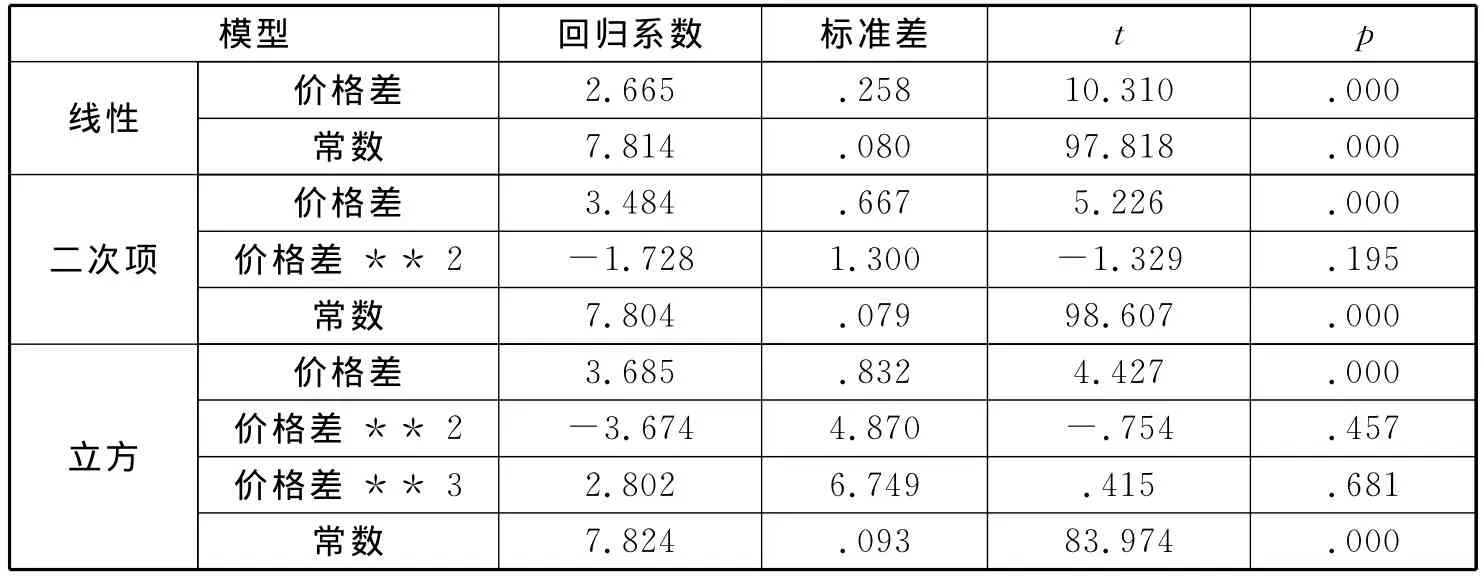
表3 价格差与销售量的曲线估计的模型系数

由表3可以看出，对三个模型系数进行显著性检验后，只有线性模型的系数均达到显著水平，而另外两种模型系数的p值至少有一个大于0．05。因此，选择线性模型最为理想，即y＝β0＋β1x2＋ε，其中x2为价格差，y为销售量，ε为随机误差，βi为回归系数。

三、模型建立与求解

（一）模型一

由曲线估计知，价格差与销售量适合线性模型，而广告费用与销售量更适合二次项曲线模型。但因二次函数可以转化为线性函数，所以可将广告费用的平方作为一个新的自变量引入，从而采用多元线性回归分析，建立价格差、广告费用、广告费用的平方与牙膏的销售量的回归模型一，即y＝β0＋β1x1＋β2x2＋β3x3＋ε，其中x1为广告费用，x2为价格差，x3为广告费用的平方，y为销售量，ε为随机误差，βi为回归系数。

多元回归分析之前，需引入新的变量。从“转换”菜单中，打开计算变量对话框，输入新的目标变量名，即广告费用的平方，然后在数字表达式中编辑函数，生成新的变量。接下来在“分析”菜单中，打开线性回归对话框，将广告费用、价格差和广告费用的平方同时选为自变量，将销售量选为因变量；单击“统计量”按钮，在弹出的对话框中勾选“置信区间”。

表4 回归模型一的模型摘要

由表4可以看出，以广告费用、广告费用的平方和价格差共同作为自变量时，能显著预测销售量，其联合解释90．5%的变异量，因此模型一从整体上来看是可用的。

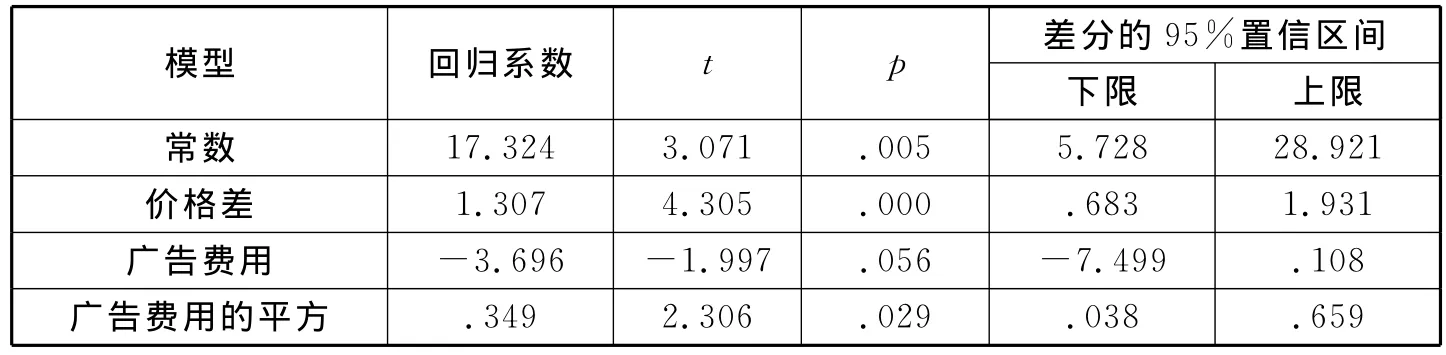
表5 回归模型一的模型系数

由表5可知，模型一的回归方程为y＝17．324－3．696x1＋1．307x2＋0．349x3＋ε。该模型显示，广告费用对销售量的影响不太显著，p值大于0．05，但广告费用的平方对销售量的影响是显著的，因此将广告费用作为回归变量仍保留在模型中。

（二）模型二

尽管模型一从整体来看较为理想，但表5显示的置信区间［－7．499，0．108］包含零点，这说明广告费用对销售量的影响导致该模型不稳定，还需要进一步改进。模型一中，广告费用和价格差对于销售量的影响是相互独立的，而由现实经验可知，广告费用和价格差之间的交互作用也可能会影响牙膏的销售量。

考察变量间的交互作用，须先对变量作定性分析。

若变量均为分类变量，则采用方差分析来检验自变量对因变量的影响以及各自变量间的交互作用；若变量均为连续变量，则采用在回归方程中纳入变量的乘积项，通过检验其回归系数的显著性来判断变量间是否存在交互作用，如果回归系数为正，则变量间存在正交互作用，如果回归系数为负，则变量间存在负交互作用；若变量包含分类变量和连续变量，可将分类变量转换为虚拟变量后，当成连续变量再进行回归分析。

考虑到广告费用和价格差均为连续变量，因此采用在回归方程中纳入二者的乘积x4来代表广告费用和价格差的交互作用，记为广告费用×价格差。具体操作如前，并在线性回归对话框中，单击“绘制”按钮，在弹出的对话框中将“＊ZPRED”选入X轴，“＊SRESID”选入Y轴，绘制标准化残差的散点图，同时勾选“直方图”，绘制标准化残差的频数分布图。

表6 回归模型二的模型摘要

表7 回归模型二的模型系数

由表6和表7知，再引入广告费用×价格差后，联合解释92．1%的变异量，较模型一有所提高，并且所有置信区间均不含零点，这说明模型二较模型一有所改进，更符合实际。模型二的回归方程为y＝29．113－7．608x1＋11．134x2＋0．671x3－1．478x4＋ε，其中x1为广告费用，x2为价格差，x3为广告费用的平方，x4为广告费用×价格差，y为销售量，ε为随机误差。表7还显示，x4的回归系数估计值为－1．478，即广告费用和价格差存在负交互作用。当价格差较大时，可以较少地依赖广告投入的增加来提高销售量；当价格差较小时，则需要投入较大的广告费用来提高销售量。

图3 残差的直方图

图4 残差的散点图

由图3可以看出，标准化残差呈正态分布。图4显示，各点围绕残差等于0的直线上下随机分布，说明当前的回归模型对原始数据拟合情况良好。

［1］姜启源，谢金星，叶俊．数学模型［M］．北京：高等教育出版社，2003．

［2］张苏江，陈庆波．数据统计分析软件SPSS的应用（五）——相关分析与回归分析［J］．畜牧与医，2003，（09）．