浅谈耗散结构理论

王晓松

（天津市南开社区学院，天津 300100）

一．问题的来源——热力学

耗散结构理论是在热力学理论处于困境的情况下提出来的，那么首先我们应当回顾一下热力学的基本理论。

（一）热力学第一定律

一个系统在不受外界影响的情况下其宏观性质不随时间变化，这个系统就被定义为热力学平衡态。系统达到了平衡态以后，仍有可能发生离开平衡态的微小偏差，这种现象叫做涨落。

如果一个系统完全不受外界影响，我们便称其为孤立系统或封闭系统。受到外界影响的系统叫做开放系统。封闭系统在经过一定时间后，势必达到热力学平衡态并长期保持下去，除非有外界影响。

如果以ΔU表示系统内能的变化，Q表示系统吸收的热量（吸收的热量为正，放出的热量为负），W为系统对外所做的功。则热力学第一定律的数学表达式为

在文字上可以表述为：在任何一个过程中，系统所吸收的热量等于系统内能的增加与对外所做功之和。

如果将系统内能扩展为一切能量，则热力学第一定律就是能量守恒与转化定律。这是因为“一切能量”必然存在于整个宇宙，“宇宙”之外无宇宙，无法流出或进入任何东西，因此就不存在吸收与释放多少热量的问题。Q＝0，因此（1）式变为：

即有多少能量，就做多少功。不存在只做功不耗能的第一种永动机。

（二）热力学第二定律

热力学第二定律说明了热力学运动的不可逆性。这一定律有两种典型的文字表述。其一是克劳修斯表述：不可能把热从低温物体传到高温物体而不引起其他的变化。其二是开尔文表述：在任一循环过程中不可能从单一热源取热使之完全转化为功而不引起其他变化。热力学第二定律所确定的热力学运动的方向是在不受外界影响下的自发过程。

热力学理论体系中还有热力学第三定律，其内容是：不能用有限的手段使系统的温度达到绝对零度。以及热力学第零定律，其内容是：如果两个热力学系统中的每一个系统都与第三个热力学系统处于热平衡（温度相同），则它们彼此也必定处于热平衡。但这些内容与本文的主题关系不大，不拟在此讨论。

（三）熵的概念及其意义

卡诺定理指出：任何一个热机的效率均不能大于工作于两个同样温度热源之间的可逆热机的效率。如果以Q1，T1表示热源1的热量和温度，以Q2，T2表示热源2的热量和温度。则根据卡诺定理，工作于两个相同热源之间的不可逆热机（适用小于号）以及可逆热机（适用等于号）的效率统一表示为：

规定吸收的热量为正，放出的热量为负，则上式可以写为

对于若干个热机，上式演变为

在更普遍的情况下，上式可以写为

1．可逆循环下熵的概念的引入

可逆循环就是完成循环而不引起其他任何变化的一种循环过程，在这种循环下（6）式演变为设循环路径中有任意两点A和B，循环从L1：AB，再经过L2：BA，就有：

也可以写成：

或者是：

这说明积分的值与积分路径无关，系统有一态函数——熵，这个态函数与上述积分的关系为：

2．可逆循环与不可逆循环的综合考量

根据

设计一个任意的不可逆循环过程，循环路径中有任意两点A和B，循环从L1：AB是不可逆过程，从L2：BA是可逆过程，这样就有：

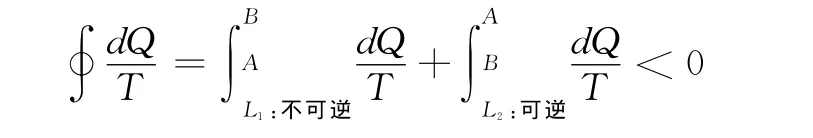
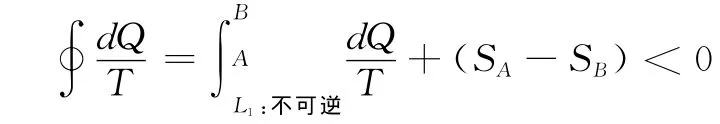
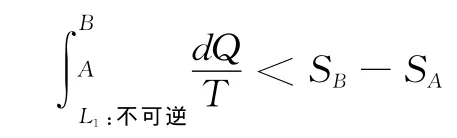
综合可逆循环和不可逆循环两种情况，总是有

3．熵增加原理

如果是绝热系统（孤立系统），无热量出入于系统，导致dQ＝0，就有

这说明在绝热过程中，系统的熵永不减少，可逆循环系统的熵不变；不可逆循环系统的熵总在增加。这就是熵增加原理。

（四）熵的概念所带来的结论

熵的概念的引入说明了不可逆过程的实质。因为如果外界对系统做功，且系统是绝热的，则外界的功转化为系统的内能。如果系统不是绝热的，外界的功可以以热量的形式传递给热源。上述一切过程中系统的熵决不可能减少，至多是不增加。宏观的规则运动（机械运动或热量的有方向的传递）转化为无序的分子热运动。即所谓的不可逆过程，就是运动向混乱度增加的方向进行，而无法向规则运动的方向回归，因此不可逆。熵就是系统混乱度的量度。从克劳修斯开始，就将热力学第二定律简单运用到了整个宇宙，得出了“宇宙的能量是不变的，但宇宙的熵趋于极大值”的结论。极大值就是宇宙达到“平衡”的状态，这时宇宙就“热死”了。也就是说，宇宙作为一个系统，由于熵的不断增加，最后也会达到无限混乱而无法发展的境地，从而灭亡。然而，所谓的能量守恒，不仅包含数量上守恒的意义，还有在其存在形式上有质的转换意义。如果能量仅能在数量上守恒而不能在存在形式上转换，就不能叫做守恒。而熵不能依靠自然界的运动来减少，却可以因为自然界的运动不断增加。要让宇宙不被“热死”，只有靠上帝。这就是恩格斯反对“热寂说”的原因。

二．对热寂说的怀疑

克劳修斯的观点使人们对宇宙的看法变得悲观，但这种观点的被瓦解并不是人们感情用事的结果。而是“热寂说”本身的非客观性造成的。

首先对“热寂说”提出诘难的是詹姆斯·克拉克·麦克斯韦（James Clerk Maxwell）。他设想有一个能被无摩擦的活门分隔成两半的容器中盛有气体。开始时，两边气体的温度和压强都相等。有一“小精灵（Maxwell Damon）”监守在活门上，他让快速分子通过活门到容器的一边，而让慢速分子到另一边。于是一边的温度越来越高，另一边的温度越来越低。“小精灵”并没有对系统做功，却使原来处于热平衡的系统有了温差，系统的熵降低了，热力学第二定律受到了挑战。1929年匈牙利物理学家西拉德（L·Szilard，1898—1964）强调指出：机器作功的关键在于妖精取得分子位置的信息，并有记忆的功能。在引入信息等于负熵的概念后，对此解释：小妖精虽未作功，但它需要有关飞来气体分子速率的信息。在它得知某一飞来分子的速率，然后决定如何操作活门后，它已经运用有关这一分子的信息。信息的运用等于熵的减少。

在“热寂说”提出后的数十年中，对其构成最大挑战的科学假说是波尔兹曼（L．Boltzmann）的“涨落说”。波尔兹曼抓住统计理论中的几率观点来批判“热寂”说。实际上他以宇宙的平衡态作为一种合理状态，但围绕着平衡态的“涨落”总是存在的。这种涨落现象并不遵从热力学第二定律。如果我们认为，这种涨落实际上是宇宙平衡态的表现形式，那么宇宙也就不可能产生“热寂”。但天文学观测表明，至今没有任何有说服力的证据证明现在的宇宙是处在热平衡态并存在着上下“涨落”。由于缺乏事实依据，“涨落说”并没有真正从科学上解决宇宙“热寂”的问题。

三．耗散结构理论的提出及其意义

由普列高京在上世纪七十年代提出的耗散结构理论显然给不可逆却没有出路的系统演化进程找到了合理的出口。这一理论指出：一个远离平衡态的非线性的开放系统（不管是物理的、化学的、生物的乃至社会的、经济的系统）通过不断地与外界交换物质和能量，在系统内部某个参量的变化达到一定的阈值时，通过涨落，系统可能发生突变即非平衡相变，由原来的混沌无序状态转变为一种在时间上、空间上或功能上的有序状态。这种在远离平衡的非线性区形成的新的稳定的宏观有序结构，由于需要不断与外界交换物质或能量才能维持，因此称之为“耗散结构”（dissipative structure）。

（一）出现耗散结构的前提条件

产生耗散结构的前提条件是系统远离平衡态。所以首先我们必须明确什么样的系统才是远离平衡态的系统。

1．处于平衡态的系统

如果系统各处可测的宏观物理性质均匀（从而系统内部没有宏观不可逆过程）的状态，我们就说这一系统处于平衡态。处于平衡态的系统有如下特性：

（1）遵守热力学第一定律。

（2）遵守热力学第二定律。上述两条定律在前面已有详细阐述，不再重复。

（3）遵守波尔兹曼有序性原理：即

即温度为T的系统中内能为Ei的子系统的比率为pi。这里是波尔兹曼因子，其物理含义是某量子态出现的热力学几率。这一因子归一化之后即为此量子态出现的数学几率。由其表达式可以看出：在一定温度下，微观运动状态出现的几率与能级有关，能级愈高，出现的几率愈小。

2．接近平衡态的系统

系统接近平衡态是指系统处于离平衡态不远的线性区，它遵守昂萨格（ONSAGER）倒易关系和最小熵产生原理。昂萨格倒易关系是不可逆过程热力学理论中的一个基本关系，其内容是：

如果我们把单位时间内通过物体单位面积所迁移的一切量（如质量、能量、动量、电量等等）统一定义为通量，以J表示，把引起迁移现象的原因统一定义为动力，以X表示，那么通量与动力成正比，即

当上述各种迁移同时发生时，通量与各种动力维持线性关系，即

如果指标i和k互换，上式也可以写作

但是对于上面两式中的系数来说，有

即只要和不可逆过程i相应的流Ji受到不可逆过程k的力Xk的影响，那么，另外一股迁移流Jk也会通过相等的系数Lik＝Lki受到力Xi的影响。后者意味着，当给定的边界条件阻止系统达到热力学平衡态（即零熵产生）时，系统就落入最小耗散（即最小熵产生）的状态。即在热平衡态下孤立系统的熵达到极大，熵产生为零。在定常耗散过程（输运、化学反应）中熵产生恒正，在线性区定常输运过程中熵产生最小，这就是最小熵产生原理。由它可推出线性区不可能形成耗散结构。

3．远离平衡态的系统

以前的物理理论认为，只有能量最低时，系统最稳定，否则系统将消耗能量，产生熵，而使系统不稳定。耗散结构理论认为在高能量的情况下，开放系统也可以维持稳定。例如生物体，以前按照热力学定律，是一种极不稳定的结构，不断地产生熵而应自行解体，但实际上生物体能不断自我完善。因为生物体是一种开放结构，能够不断从环境中吸收能量和物质，而向环境放出熵，以此保持自身系统的稳定。

（二）子系统间的非线性相互作用

这是系统产生耗散结构的内部动力学机制，正是子系统间的这种相互作用，使在临界点处，微涨落被非线性机制放大为巨涨落，使热力学分支失稳，在控制参数越过临界点时，非线性机制对涨落产生抑制作用，使系统稳定到新的耗散结构分支上。如果没有非线性机制，系统将平稳地通过临界点，继续进行缓慢的变化而不会产生质变。

（三）开放系统

热力学第二定律告诉我们，一个孤立系统的熵一定会随时间增大，熵达到极大值，系统达到最无序的平衡态，所以孤立系统绝不会出现耗散结构。那么开放系统为什么会出现本质上不同于孤立系统的行为呢？这是因为在开放的条件下，系统的熵增量dS是由系统与外界的熵交换dSe和系统内的熵产生dSi两部分组成的，即：

热力学第二定律只要求系统内的熵产生非负，即dSi≥0，然而外界给系统注入的熵dSe可为正、零或负，这要根据系统与其外界的相互作用而定，在dSe!0的情况下，只要这个负熵流足够强，它就除了抵消系统内部的熵产生dSi外，还能使系统的总熵增量dS为负，总熵S减小，从而使系统进入相对有序的状态。所以对于开放系统来说，系统可以通过自发的对称破缺从无序进入有序的耗散结构状态。

（四）子系统的涨落

一个由大量子系统组成的系统，其可测的宏观量是众多子系统的统计平均效应的反映。但系统在每一时刻的实际测度并不都精确地处于这些平均值上，而是或多或少有些偏差，这些偏差就叫涨落，涨落是偶然的、杂乱无章的、随机的。在正常情况下，由于热力学系统相对于其子系统来说非常大，这时涨落相对于平均值是很小的，即使偶尔有大的涨落也会立即耗散掉，系统总要回到平均值附近，这些涨落不会对宏观的实际测量产生影响，因而可以被忽略掉。然而，在临界点（阈值）附近，情况就大不相同了，这时涨落可能不自生自灭，而是被不稳定的系统放大，最后促使系统达到新的宏观态。

（五）耗散结构理论的现实意义

耗散结构理论在自然科学和社会科学诸多方面均有广泛应用，在此无法逐一陈述。就我们所在的成人教育与职业教育系统而言，耗散结构理论就有明显的现实意义。近年来，随着人口出生率的下降和教育事业的迅速发展，成人教育和职业教育院校普遍面临招生难，发展缓慢的问题。学校就是一个典型的耗散结构，如果无法与社会进行人员、资金、设备和信息的交换，变成了“孤立系统”，必将导致其内部熵的有增无减，管理难度越来越大，后果不好预测。要想改变这种局面，必须改变教学思维，提高教学质量，重新赢得生源。同时整合教学资源。尤其是要改变教师的“单位所有制”，使教师队伍能够真正流动起来。总之，要使成职教院校真正变成“开放系统”，这些学校才有健康发展的可能性。

［1］熊吟涛著．热力学［M］．北京：人民教育出版社，1982．

［2］马文蔚著．物理学［M］．北京：高等教育出版社，2011．