储油罐的变位识别与罐容表标定之建模与分析

董春芳

（天津冶金职业技术学院，天津 300400）

一、引言

（一）问题简介

2010年全国大学生数学建模竞赛A题所提出的问题实际是一个对产生变位的油罐的罐容表重新标定的问题，即建立模型计算油罐变位对罐内油量测定的影响，然后再给出油位高度间隔为定值的罐容表标定值。问题一是研究小椭圆型储油罐，分别对罐体无变位和倾斜角为α＝4．1°的纵向变位两种情况建立模型，再对罐体变位后油位高度间隔为10cm的罐容表进行标定。问题二是研究实际模型，通过建立模型，确定所给数据的罐体倾斜和横向旋转角度α和β，再对罐体变位后油位高度间隔为10cm的罐容表进行标定。本文将主要处理上述两个问题。

（二）模型假设及其符号说明

1．基于所考虑的问题，建立如下合理的假设

（1）油罐有变位和无变位时，单位油位高增长进出油管、油位探针被油浸没体积增长量相同。

（2）油罐的倾斜角度α和油罐的旋转角度β都很小。

（3）油罐位移过程中形状不发生变化。

2．符号说明

（1）a－椭圆柱底面长轴长（单位：m）

（2）b－椭圆柱底面短轴长（单位：m）

（3）d－椭圆柱高（单位：m）

（4）h－油罐油高（单位：m）

（5）S－椭圆柱罐体理论油柱底面积（单位：m2）

（6）V－油罐体理论储油体积（单位：m3）

（7）ΔV－椭圆柱罐体储油体积误差值（单位：m3）

（8）V修无变位椭圆柱罐体修正储油体积（单位：m3）

（9）V出椭圆柱罐体出油体积（单位：m3）

（10）α－变位油罐纵向变位角度（单位：°）

（11）V变－变位椭圆柱罐体理论储油体积（单位：m3）

（12）V变修－变位椭圆柱罐体修正储油体积（单位：m3）

（13）R－球罐体圆柱横截面半径（单位：m）

（14）r－球罐体两边球冠球半径（单位：m）

（15）h0－变位球罐体实测油面高（单位：m）

（16）β－变位油罐横向变位角度（单位：°）

（17）V实－球罐体实际储油体积（单位：m3）

二、简化小椭圆型储油罐模型的求解

本章主要分析简化模型，即小椭圆型储油罐在不同情况下罐内储油量与油位高度的理论及实际关系。采用的主要方法是多重积分及曲线拟合。假设底面椭圆的长轴，短轴，柱体的高及油高分别为a，b，d，h，其中a＝0．89m，b＝0．6m，l＝2．45m

（一）罐体无变位时罐内储油量与油位高度关系

1．理论模型建立

当罐体无变位时，罐内的油量所呈现的形状仍是很直观很规则的柱体，其高仍是d。下面通过分析其侧切面面积，进而得到其体积。在椭圆柱体罐体的一侧切面上建立平面直角坐标系，坐标原点取做椭圆的中心，x轴沿长轴方向，y轴沿短轴方向。设油面与y轴相交于点（0，l），如图2．1所示。显然l＝h－b。

易知油柱体截面面积为

从而可知无变位时油罐体积V为：

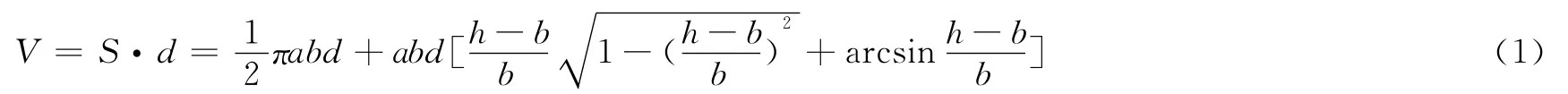
2．模型修正及误差分析

（1）式即为理论上的无变位罐内储油量随着油位高度而变化的模型。但实践中由于受到许多外在因素的影响，使得实测的结果与理论算出的结果会产生一定的误差，下图2．2即为在同一组油位高度数据下，式（1）得到的（h－V）曲线与已知实测进油数据得到的（h－V）曲线的误差比较图2．2。

通过图2．2可以看到计算得到的数据与测量数据确实有误差，并且误差随油位高度的增长而增大，我们分析这些误差应该是因为忽略了测量探针，输油管和出油管的体积所导致。为修正这些误差，我们采用三次多项式进行拟合，得到一个误差的补偿函数，运用Matlab软件及已知的实测数据和理论数据，拟合出误差函数如下：

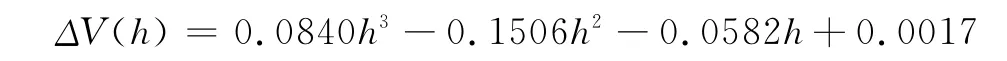
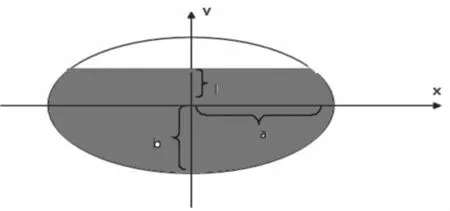
图2．1 罐体截面示意图

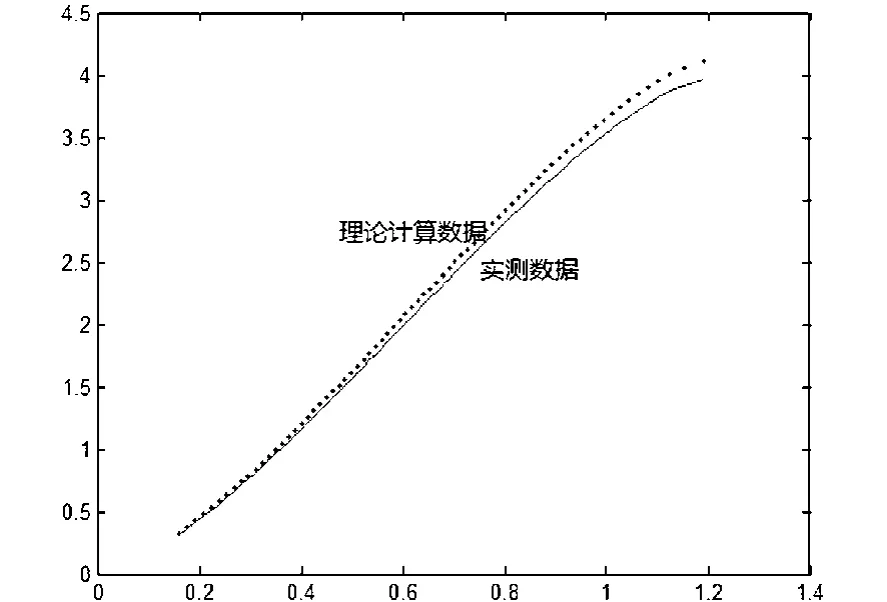
2．2 无变位计算数据和实际测量进油数据误差比较图

于是可以得到无变位时储油量与油位高度关系的修正模型：

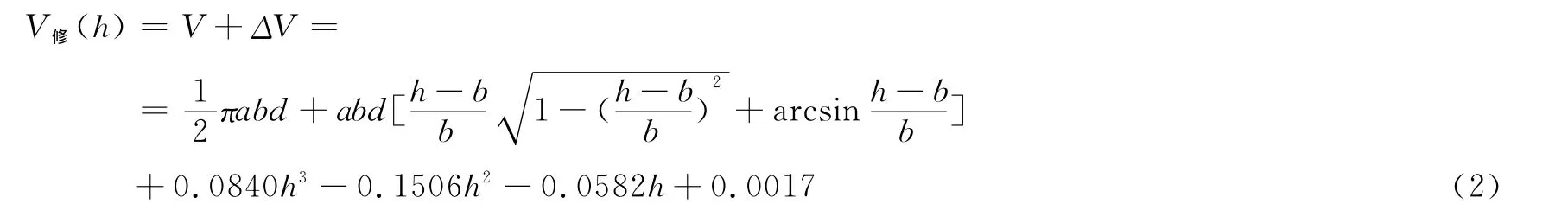
为了验证模型（2）的有效性，我们采用出油数据进行检验，计算并作图，修正后模型（2）

计算的数据与实测出油数据（h－V出）的比较图为图2．3。

从图2．3中可以看到两组数据十分接近，最大误差为4．4722e－004，可见模型（1）通过增加补偿函数确实得到了很好的修正，是合理的。

（二）罐体发生变位时罐内储油量与油位高度关系

1．模型建立

当储油罐发生纵向倾斜变位，其倾角为α＝4．1°时，建立三维直角坐标系，使得z轴沿油位探针竖直向上，y轴沿储油罐各横截椭圆面中心，x轴过油位探针所在椭圆截面的长轴，构成右手系，如图2．4所示的yoz平面

储油罐底面的椭圆方程为

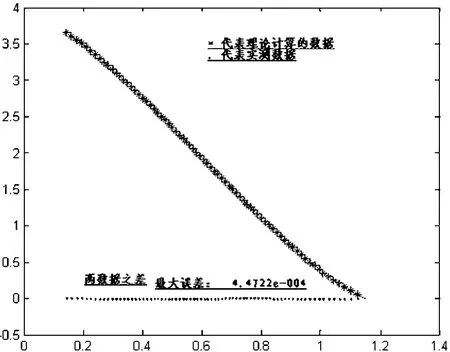
图2．3 修正模型无变位测量数据和实际测量出油数据误差比较图

图2．4 平面示意图

其中a＝0．89，b＝0．6。由2．4图可知，右面与yoz平面相交的线段所在yoz平面上的直线方程是

注意到，当直线过 （0，z），z!－0．6时，h＝0，易知当油面过点 （0，0，－0．6）时的油量体积为

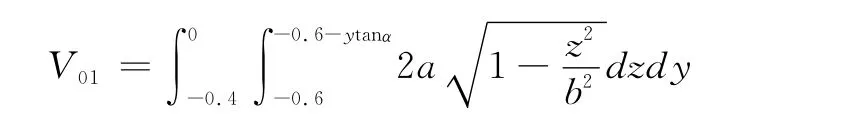
从而易知，当V!V01时均有h＝0。

而当直线过（0，z），z≥0．6时，h＝1．2，此时的临界体积将分不同的情况讨论给出结论

由于储油罐纵向发生变位，罐内油所占部分形状因油位高度变化而变化，使得一般油量体积不能轻易求得，因此必须对油位高度分段考虑，为方便计，我们以油面与z轴相交位置分段考虑，分三种情况讨论，得到V随h的变化而变化的理论公式为：

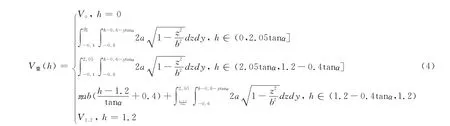
2．模型修正与误差分析

实际中有很多种因素会造成油罐测量体积的误差，如压力变化、温度变化、测量仪器磨损以及输油管和油位计排开部分体积等因素，一般可以认为误差是由以上几方面因素共同作用的结果，但有资料数据显示，产生误差的主要因素是储油罐内油的自重对储油罐的压力过大使其产生了形状的改变。

修正模型时将以实测数据中的进油数据做为修正模型的依据，最后以出油数据来检测我们的修正模型是否可行。

注意到，实测进油数据里，进油前油罐里有一定的油量，油罐计量显示为215L，但这并不是油罐里的实际油量值，而是油罐无倾斜时的油位所显示的油量值。因此，我们需要做一个转换。首先我们运用数值筛选法及2－1中的修正模型，得到215L所对应的油位刻度近似为123．3mm，将其带入模型（4）即可得油罐里的实际有油量约为105．8L。在油罐发生倾斜角为α＝4．10的纵向变位情况下，油罐由于非均匀变形以及2－1中分析的一些因素影响下，理论模型（4）计算所得数据难免与实测数据之间存在一定的误差。下图即为理论计算数据与已知实测进油数据之间的误差对比图2．5。

图2．6表明计算得到数据与测量进油数据确实有误差。为修正这些误差，我们采用三次多项式拟合，给出一个误差的补偿函数。运用Matlab及已知实测数据和理论数据，拟合出函数如下：

ΔV（h）＝0．2881h3＋1．0257h2－1．0224h＋0．1129于是可以得到变位时储油量与油位高度关系的修正模型：

为了验证模型（5）的有效性，利用模型（5）和出油数据计算并作出修正后计算的数据与实测出油数据（h－V出）的比较图2．6。

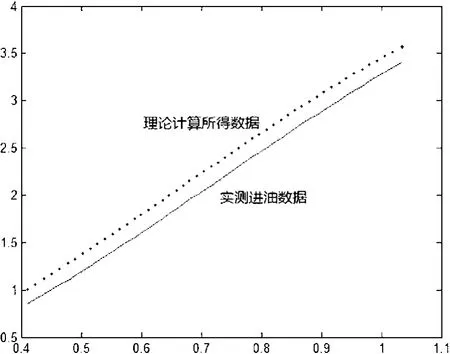
图2．5 变位时计算数据和实际测量进油数据误差比较图

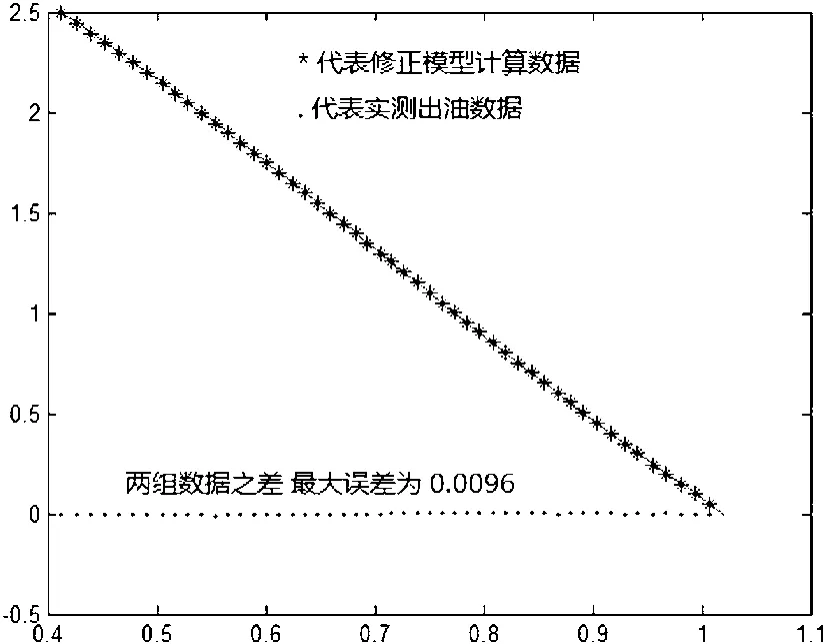
图2．6 补偿后变位测量出油数据和计算数据2误差比较图

从图2．6中可以看到两组数据十分接近，最大误差为0．0096，可见模型（4）确实得到了很好的修正，进一步说明增加补偿函数是合理的。

三、实际带球冠储油罐模型

本章将对实际油罐模型，即带球罐的储油罐模型分析其罐内储油量与油位高度的理论及实际关系。采用的方法是多重积分，数值积分及曲线拟合。记圆桶横截圆半径，两边的球罐球半径，实测油面高度，油面实际高度，纵向角度及横向角度分别是R，r，h，h0，α，β。

（一）罐体变位时罐内储油量与油位高度及横向、纵向角度的理论模型

此时的问题多了一个横向偏斜。对此我们建立三维直角坐标系，使得z轴过油位探针所在横截圆圆心垂直于油面竖直向上，y轴沿圆桶各横截圆面圆心，x轴过油位探针所在圆截面指向横向偏斜向上的方向，构成右手系，如图所示yoz平面图及xoz平面图。

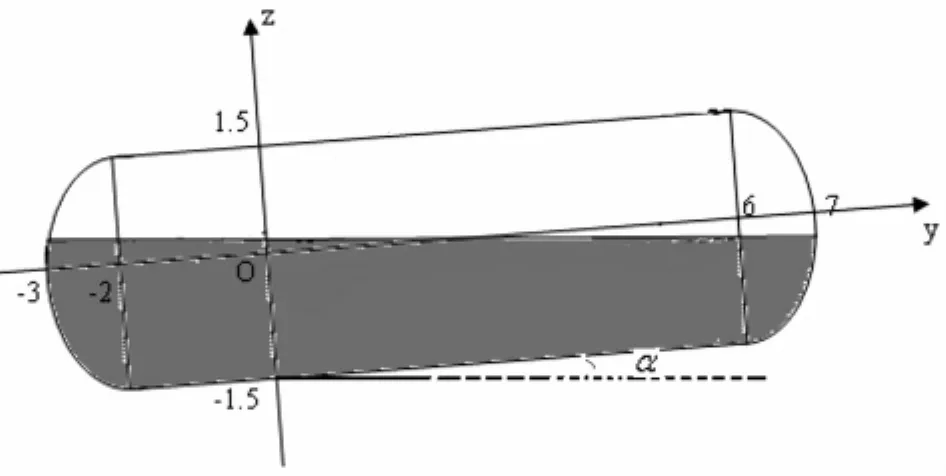
图3．1 油罐纵向变位后的平面图

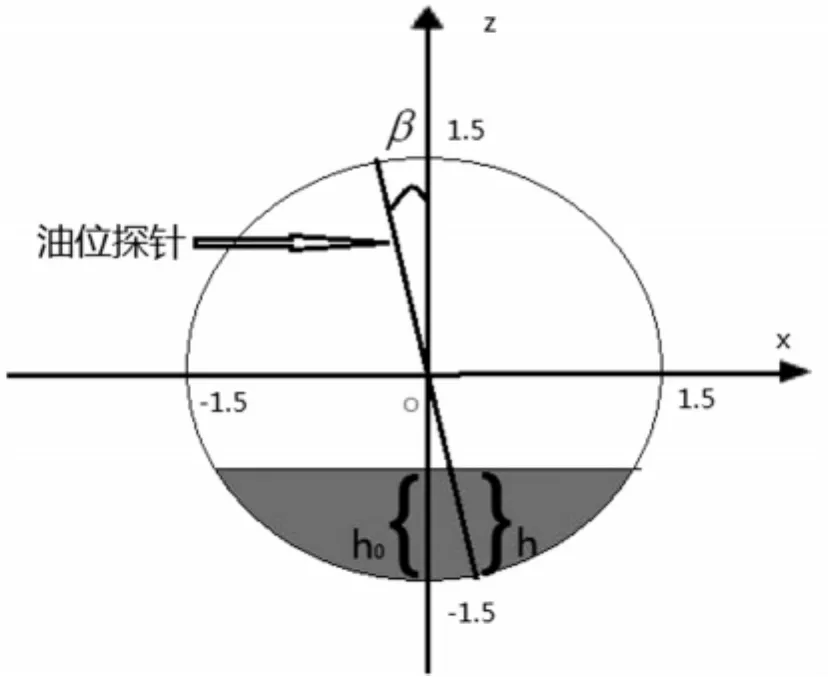
图3．2 油罐纵向变位后的平面图

经简单分析可知此时油面与平面相交的线段所在平面上的直线方程是

其中h0＝R－（R－h）cosβ。

当直线（6）过 （0，z），z!－Rcosβ时，h＝0，且易知当油面过点 （0，0，－Rcosβ）时的油量体积为

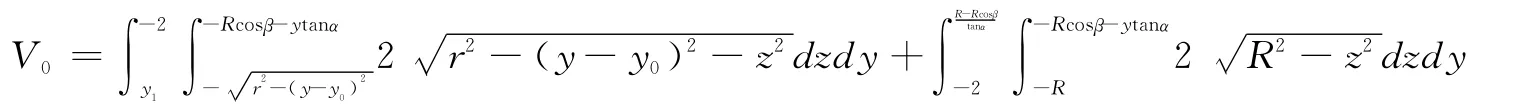
其中

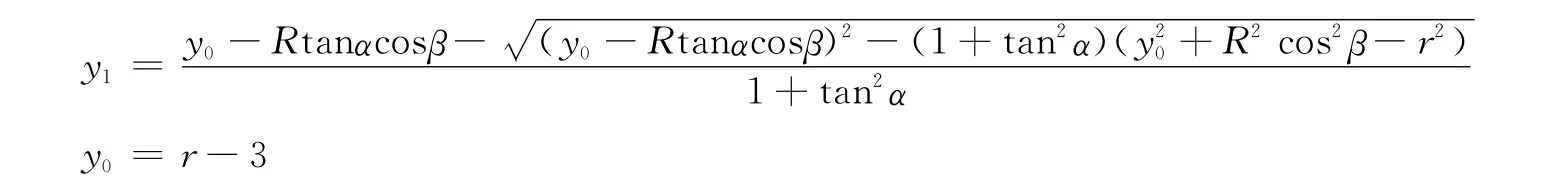
从而可知，当V!V0时均有h＝0。

而当直线过（0，z），z≥Rcosβ时，h＝3，此时的临界体积将分不同的情况讨论给出结论。

与第一章中的简化模型一样，由于储油罐纵向发生变位，罐内油所占部分形状因油位高度变化而变化，使得一般油量体积不能统一求得表达公式，因而得对油位高度分段考虑，为方便计，我们仍以油面与z轴相交位置分段考虑，分六种情况讨论，给出在发生纵向和横向变位时，实际油罐储油量V随油位高度h，纵向偏斜角度α及横向偏斜角度β变化的理论模型（7）。

（二）理论模型的修正及误差分析

本节中，我们将运用最小二乘法，及分段分步长搜索法，结合实测数据对上节中得到的理论模型（7）找到实测模型的偏斜角度α，β。最后再将得到的角度带回模型（7）并将其应用到另一组实测数据中检验所得结果的有效性。

由于实际罐内油量初值未知，所以罐内储油量的准确值是未知的。由实测数据可以知道不同时刻出油的出油量ΔVi＊，同时可以由模型（7）的V＝V（α，β，h）计算得到相应的实际储油量的改变量ΔVi＝V（α，β，hi－1）－V（α，β，hi），该问题可以归结为求解非线性最小二乘问题：

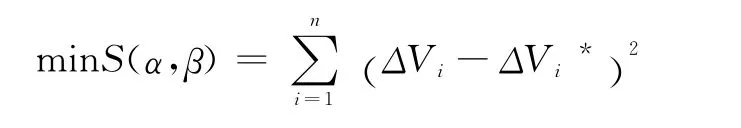
其中

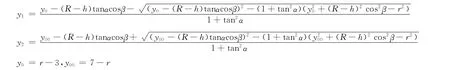
用分段搜索与变步长搜索相结合的算法，运用Matlab编程最后计算得到α＝2．1°，β＝4．4°。且此时

将α＝2．1°，β＝4．4°带入模型（7），即得到实际球罐的真实模型

为了进一步验证模型（8）的有效性，我们结合第二段实测数据，运用Matlab作出下面的理论与实测出油数据比较图，由图3．3可以看出，理论计算的结果与实测数据也是相对吻合的，最大误差控制在0．0028范围内，因此说明实际模型（8）是有效的。

四、结论

本文中，我们先后研究了椭圆型储油罐和实际油罐模型分别在不变位和发生变位时，罐中储油量与油位高度及偏斜角度之间的关系，并给出了初始理论模型，然后结合实测数据得到最后的能够用于实践的修正模型。

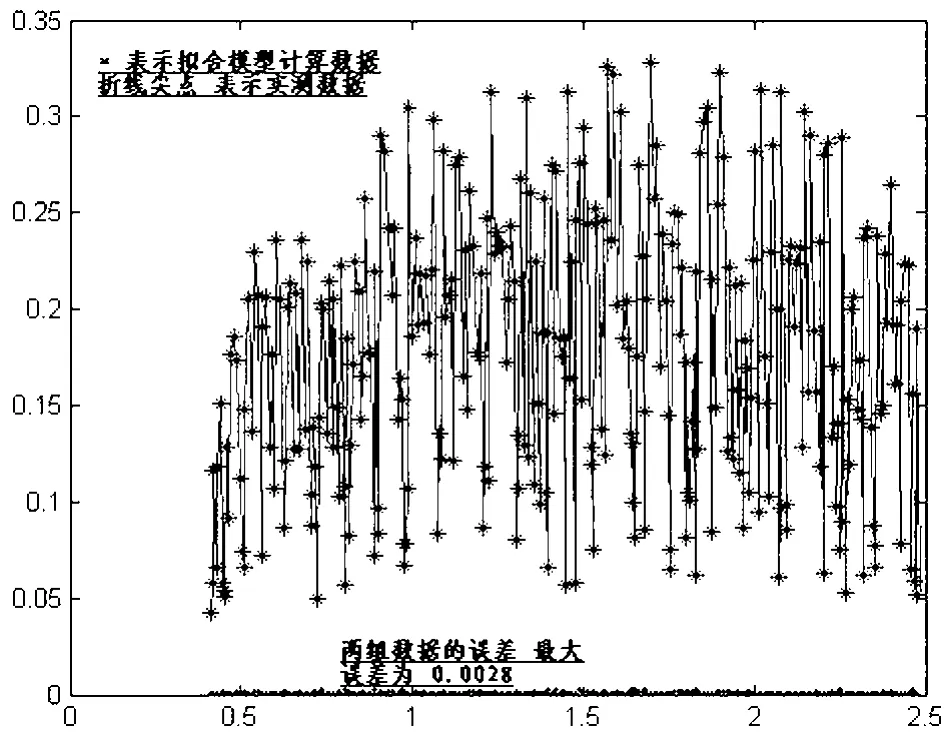
图3．3 模型（8）的有效性验证图

在第二章中，我们给出了简化油罐的理论分析模型，结合进油的实验数据，对理论模型进行了误差修正，从而得到了比较准确的实际模型（2），并利用出油的实验数据对模型（2）进行了检验，得到误差为4．4722×10－4，说明修正模型合理。

当椭圆储油罐罐体发生纵向变位α＝4．1°时，油位高度间隔为10cm的罐容表标定值。

表1 小椭圆罐的修正罐容表的部分结果（α＝4．1°）

实际带球冠罐体变位后（α＝2．1°，β＝4．4°）油位高度间隔为10cm的罐容表标定值。

表2 变位后储油罐的修正罐容表部分结果（使用参数α＝2．1°，β＝4．4°）

值得指出的是，由前所述，实际储油罐在使用过程中，由于各种因素相互作用总会发生变位（主要是横向和纵向的变位），而且这些因素是随着时间而一直持续着的。因此长时间使用总是需要对油位高度进行定期重新标定的。

我们的模型只是给出了在定期某次标定的一种标定的方法，为了更科学地给出储油罐的油量准确标定方法，我们提出下面更为系统的方法：

（1）定期对油罐的进出油量和油高做好对应记录，保持实测数据的持续性。

（2）定期利用本文建立的模型（7）计算出相应的横向和纵向变位角度，以便于观察对油罐进行重新标定的周期和时间。

（3）一般来说，重新标定的周期是稳定的，如果短时间发现算出的变位角度变化波动很不稳定时，说明储油罐受到了某些因素的较大影响，此时是需要对其进行全方位的检查和整修。

［1］乐经良．数学实验［M］．北京：高等教育出版社，1999．

［2］田乐军．倾斜式罐椭圆部分容积近似计算［J］．现代测量与实验室管理，2004，（01）．

［3］王宪杰，侯仁民．高等数学典型应用实例与模型［M］．北京：科学出版社，2005．