Fejer不等式的注记
程海来
(合肥工业大学数学学院,安徽合肥230009)
1893年Hadamard提出了如下著名不等式[1],即
定理1若f(x)为区间a,b上的凸函数,则有
(1)
国内外很多学者对此不等式做过研究和推广,如[2-5]等,其中Fejer得到了如下结果(可见[2]).
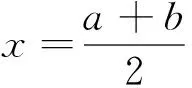
(2)
本文在较弱条件下得到了(2)的加强形式,亦即有如下的
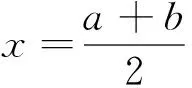

(3)
证先证明左边不等式.由f(x)带Lagrange余项的Taylor公式,
(4)
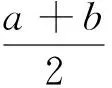
于是有
(5)
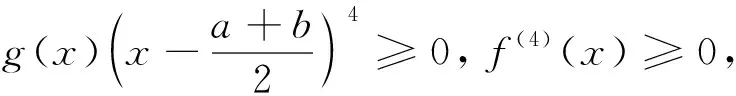
(6)
由带积分余项的Taylor公式,
(7)
(7)式两边同乘以g(x)并对x从a到b积分,由对称性可知,
故有
(8)
再由(7)知
(9)
于是
(10)
8-10,得
(11)
由于

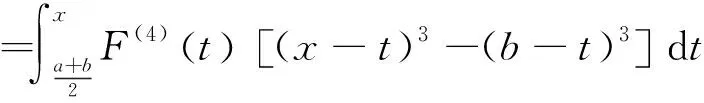
而F(4)t≥0,(x-t)3-(b-t)3≤0,(b-t)3≥0,所以
从而由(11),有
(12)
由(6),(12)知不等式(3)成立.
若在a,b上f″(x)≥0,则f(x)为a,b上的凸函数,在定理3的条件下,由(3)可知
故不等式(3)为(2)的加强形式.
特别在不等式(3)中取g(x)≡1,则有
推论设函数f(x)在a,b上有连续4阶导数且f(4)(x)≥0,则有
(13)
若在a,b上f″(x)≥0(此时f(x)为a,b上的凸函数),易知不等式(13)为(1)的一个加强.
[参 考 文 献]
[1] Hadamard J.Etude sur les propriétés des fonctions entières et en particulier d’une fonction considérée par Riemann[J]. J Math. Pures Appl.58 (1893), 171.
[2] Fejér L. Uber die Fourierreihen, II[J]. Math. Naturwiss Anz. Ungar. Akad. Wiss,1906,21:369-390 (In Hungarian).
[3] Wang Zhong-li and Wang Xiang-hua. On an extention of Hadamard inequalities for convex functions[J]. Chin.Ann of Math,1982,3(5):567-570.
[4] 冯慈璜.关于关于凸函数的 Hadamard 不等式[J].数学年刊(中文版),1985,6 (A ):4,443-446.
[5] 于永新,刘证. 凸函数的几个Hadamard型不等式[J]. 数学的实践与认识, 2005,35(1):201-207.

