爆炸荷载下盾构管片的动力响应分析

刘 扬， 宋春明， 卢 浩

(解放军理工大学 国防工程学院, 南京 210007)

地铁反恐问题研究已成为全球的热点问题，对于地铁隧道管片结构，超过60%的威胁来自爆炸袭击。鉴于此，开展地铁隧道管片结构抗爆问题研究，具有很重要的理论及实际应用意义。

当前对爆炸荷载作用下隧道结构的动力响应、变形和破坏分析方面的研究已取得了一定的进展，主要方法有模型试验、理论分析和数值模拟。孔德森等[1]针对南京地铁区间隧道的实际工程地质条件，建立了地铁隧道的冲击反应计算模型和各种材料的模型，采用流固耦合算法，对10kgTNT炸药作用下地铁隧道的冲击反应进行了全面研究。刘齐建等[2]对径向谐和激励下圆形隧道的动力稳定性进行了研究，从动荷载下衬砌结构的振动方程出发，得到了隧道衬砌动力失稳临界频率计算公式，对可能影响隧道衬砌动力稳定性的因素进行了参数分析，探讨了系统参数对衬砌动力稳定性的影响。刘沐宇等[3]以武汉长江隧道为工程依托，通过ANSYS/LS-DYNA软件建立爆炸荷载作用下盾构隧道的动力响应模型，对行车道板中部上缘不同孔径的接触爆源发生爆炸事故时盾构隧道衬砌结构各部位的动力响应进行分析。马立秋等[4-5]采用清华大学50g-t土工离心机进行浅埋圆形结构物在地表爆炸条件下的试验研究，研究不同炸药量、不同结构物埋深、不同覆盖层材料、不同土层含水量等情况下地下结构物的动力响应。刘干斌等[6]以拟建宁波轨道交通建设工程盾构隧道为背景，在设定爆炸当量的基础上，通过数值模拟获得爆炸应力波在软土中的传播规律、隧道周围不同点压力、隧道衬砌结构速度和加速度时程曲线。Karinski等[7]建立了地下连续介质中多段衬砌动态弹塑性分析模型，将衬砌看作由碳素性铰链连接的刚性管片连接，考虑了围岩介质的粘弹性，得到了管片角加速度递推方程，分析了地基参数对管片结构动力响应的影响。

求解地铁管片结构在爆炸荷载下的破坏响应时，管片结构及其周围介质在初始地应力场作用下的应力和变形形态至关重要。罗昆升等[8-9]将模型简化为二维模型进行计算，并将模拟计算结果映射到相应三维模型中，再考虑锚固螺栓初始预紧力的影响，求解得到了地铁管片结构的初始应力和应变状态，并对不同埋深状态的管片结构初始地应力进行了计算比较。王苏等[10]基于ABQUS软件，将极限剪应变作为破坏标准，采用生死单元法模拟了地下结构的地震破坏过程，通过结构埋深考虑了初始地应力对地下结构抗震性能的影响。

本文在文献[7]的基础上，考虑管片间及管片与土体间的相互作用，通过静力分析求得初始地应力，将所得内力作为动力分析的初始状态，之后进行动力响应分析，通过与有限元分析结果的对比验证了方法的合理性。

1 计算模型

1.1 基本假设

管片连接螺栓是管片结构在爆炸荷载作用下最易发生破坏的部位，单个管片的刚度比连接处的螺栓刚度要大许多，因此可以忽略管片的变形，将管片假设为刚体。

1.2 爆炸荷载的确定

土中爆炸荷载作用在结构上荷载的计算，要考虑介质与结构的相互作用。根据荷载确定方法，首先计算作用在地下结构上的应力自由场分布形式和规律，然后依据介质与结构相互作用原理，利用综合反射系数，得到作用在结构上的荷载。

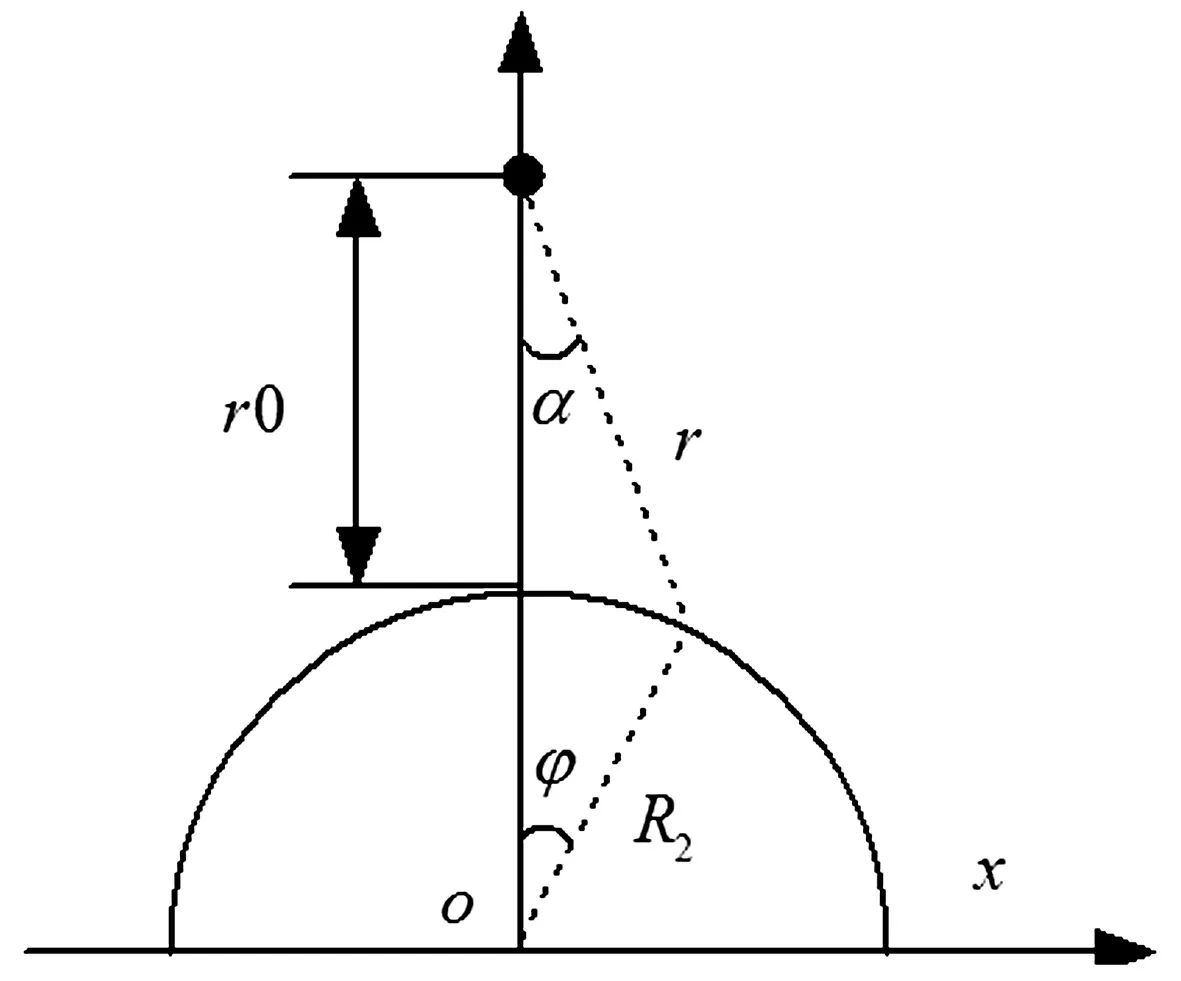
图1 模拟工况示意图

图1为迎爆面示意图，图中R2为管片外半径，r0为爆心至管片拱顶点垂直距离，r为爆心至管片环向各点的距离。

TM5-855-1公式[11]能够反映不同介质中的耦合效应、不同介质波传播特性差异以及地冲击衰减的差别，是较常使用的自由场峰值应力计算公式。本文采用该公式进行计算：

(1)

(2)

(3)

式中，p0为峰值压力；β为系数(与介质材料有关)，取0.47；f为爆炸耦合系数；ρ为介质密度；c为波速；ρc为介质材料的声阻抗；R为装药距所求点的距离；W为装药重量；n为衰减系数；t0为爆炸应力波传播到某一给定点的时间；tr为压缩波升压时间。

对于管片外表面上任意一点，荷载到达的时间、压力峰值与正压时间均不同，应力峰值沿管片表面分布表达式为[12]

pm=p0KeKOTPKσ

(4)

式中，Ke为衰减系数；Kσ为侧压力系数；KOTP为广义反射系数。KOTP的表达式如下

(5)

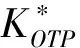
(6)

式中τi为荷载的持续作用时间。

2 初始静力分析

求解隧道管片结构在爆炸荷载作用下的动力响应时，管片结构及其周围介质在初始地应力场作用下的应力和变形状态至关重要。许多情况下，此类问题中围岩在未受到动力荷载作用以前可能已经出现了变形，还有一些情况，地下结构原来是按静力荷载条件进行设计的，后来需要考虑其在动力荷载作用下的变形与破坏问题，所有这些问题都要求在进行动力分析以前，准确的确定围岩和结构的初始应力和变形状态。

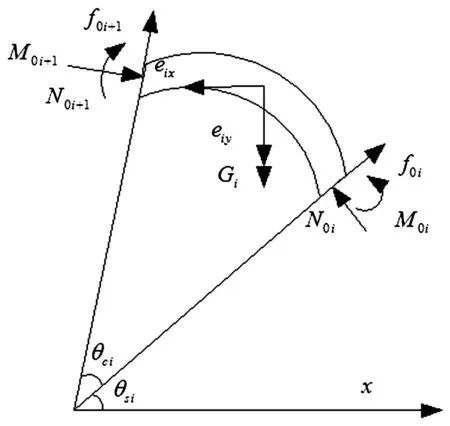
图2 管片静力分析示意图

没有施加动荷载以前，螺栓上的应变很小，没有达到屈服极限，因此，在管片初始平衡状态时，忽略环向螺栓的剪切力。管片i初始静力平衡状态的受力情况如图2所示，由x和y方向力的平衡和弯矩平衡，得到

-(F0+N0i)sinθsi+(F0+N0i+1)sin(θsi+θci)+f0icosθsi+f0i+1cos(θsi+θci)-eix=0

(7)

(F0+N0i)cosθsi-(F0+N0i+1)cos(θsi+θci)+f0isinθsi+f0i+1sin(θsi+θci)-Gi-eiy=0

(8)

M0i+1-M0i-eixR0sin(θsi+θci/2)+N0i+1R0-N0iR0+(eiy+Gi)Rcos(θsi+θci/2)=0

(9)

式中，θci为管片圆心角；θsi为管片右端轴线与x轴的夹角；R0为中心半径；N0i为管片环间压力；f0i为管片环向接触面上的静摩擦力；F0为环向螺栓的初始紧固力；Gi为管片的自重；eix、eiy为管片上所受土压力在x和y方向的分量。

静摩擦力f0i与管片环向间的压力N0i的关系可表示为

f0i=k1×(N0i+F0)

(10)

k1为静摩擦系数。

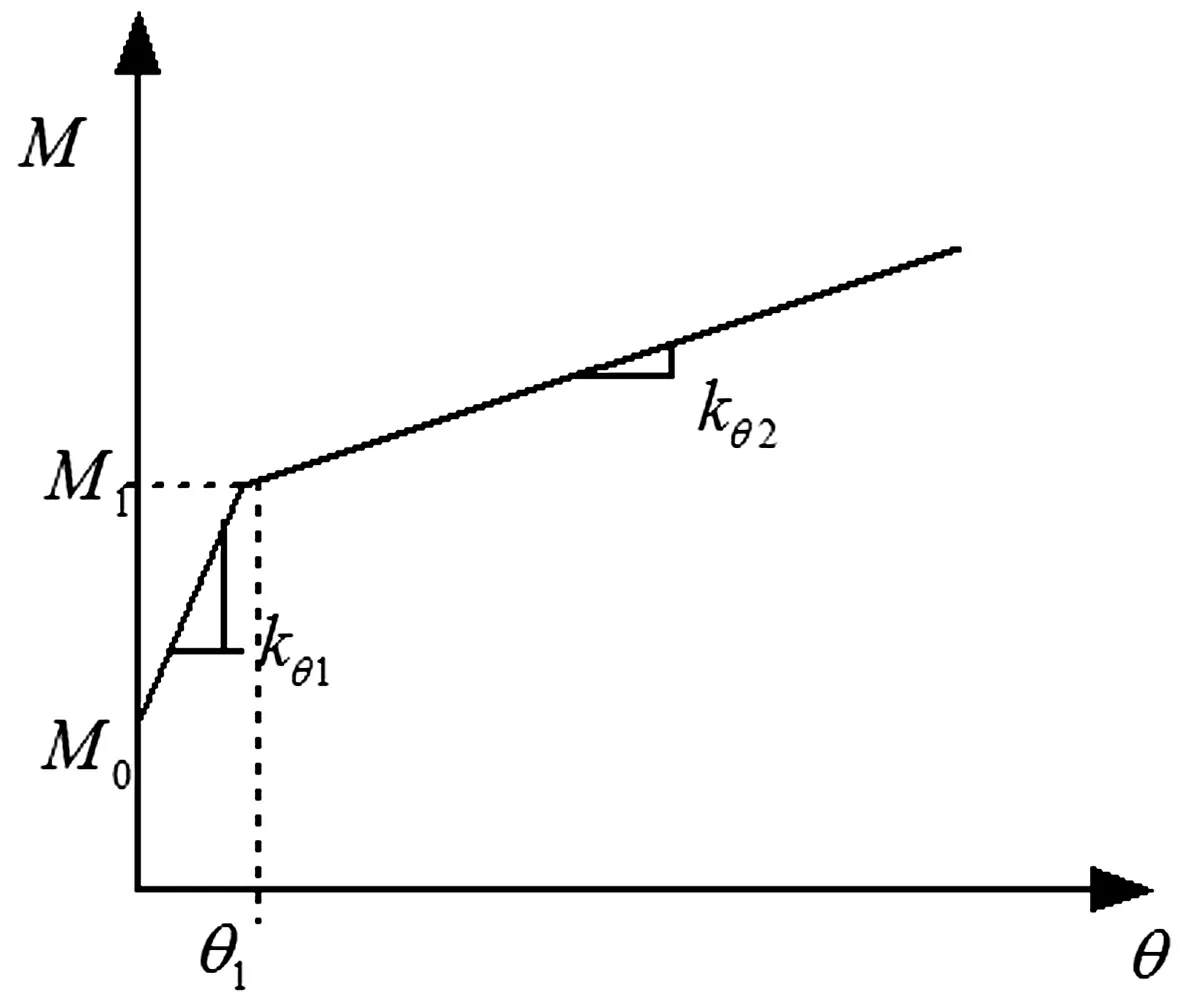
图3 双直线接头刚度模型

管片间的弯矩由管片间的相对转角决定，基于文献[13]提出的双直线模型(图3)可得

(11)

式中，kθ为接头抗弯刚度，根据定义求得；M0为初始转动弯矩；M1为转折点弯矩。在接头构造已知的情况下，M0、M1都是轴力N的函数，根据以下公式求得：

M0=a0N+b0

M1=a1N

(12)

式中，a0、a1、b1为待定参数，与接头轴力N，管片接头构造，传力衬垫尺寸和变形模量，螺栓预紧力等因素有关。

由式(7)～式(9)可算出初始状态下管片间的接触力，可直接作为初始条件加入到后续管片运动微分方程中。

3 爆炸荷载作用下管片受力分析

3.1 管片受力分析

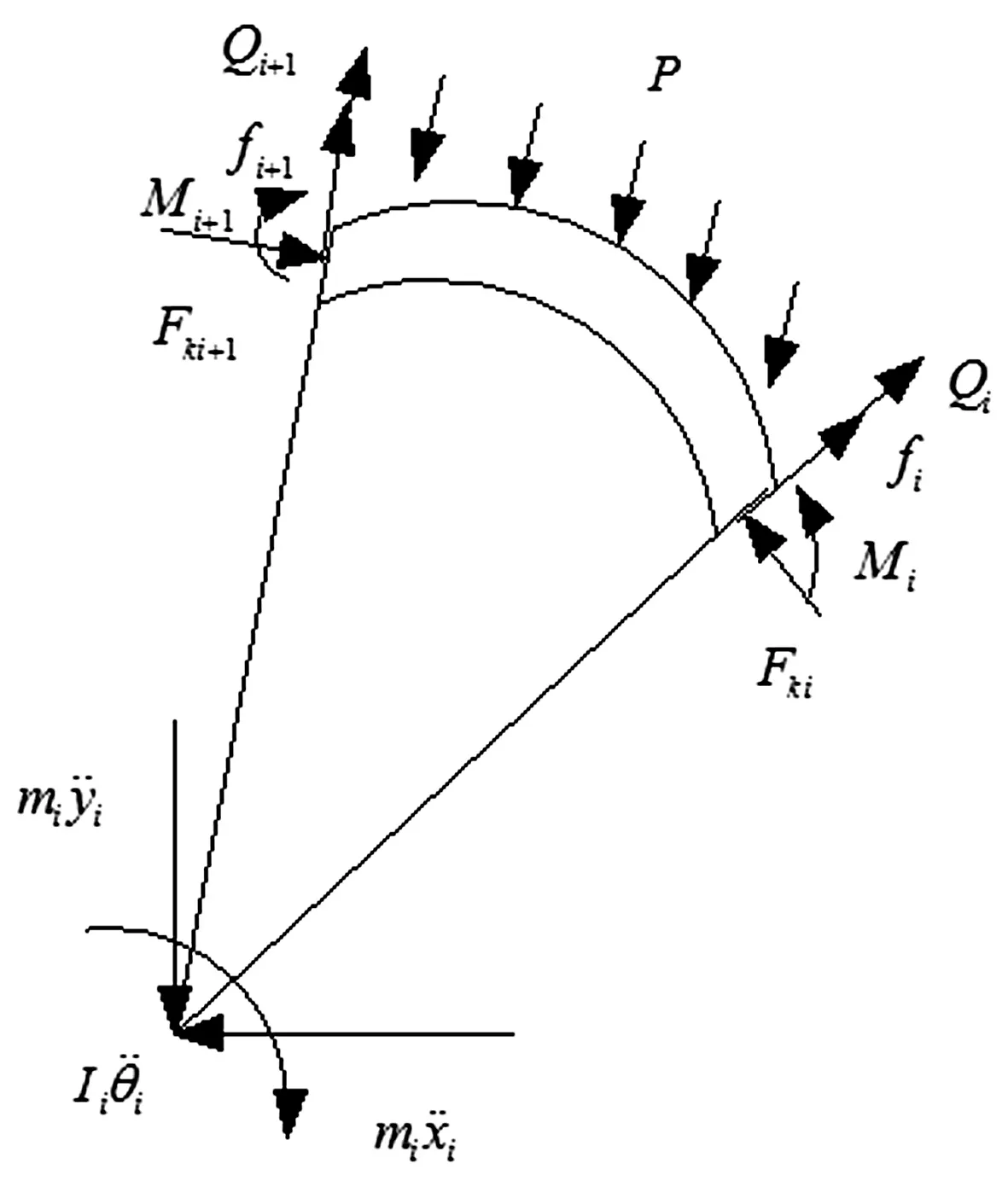
图4 管片结构受力示意图

在土中爆炸冲击波的作用下，管片与管片、管片与螺栓、管片与土体间都将产生相互作用。另外，管片和螺栓对冲击荷载的抵抗作用方式也不同，管片主要受惯性作用，其变形不大；而螺栓与管片相比由于刚度很小，因此其变形相对较大(包括螺栓的拉伸变形和管片之间错缝引起的剪切变形)。单个管片在爆炸荷载作用下的受力情况如图4所示，图中p(t)为管片外表面作用的入射爆炸荷载，沿管片径向作用。管片环间的相互作用力为：

Fki=N0i+kn[r(t)-r0]

(13)

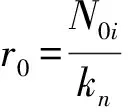
螺栓和管片间相互作用力为：

Qi=τA=GAγ

(14)

管片与围岩接触时，在接触面将传递切向力和法向力，在分析中应考虑阻止表面相对滑动的摩擦力。环向管片间的动摩擦力为：

fi=k2Fki

(15)

式中,k2为接触面间的动摩擦系数。

管片间的弯矩由上节提出的双直线模型可得。对于管片外表面上任意一点，荷载到达时间、压力峰值和正压时间均不同，为了求解管片外爆炸荷载随时间的变化关系，采用数值积分的方法求解。p(t)为管片上任一点荷载，管片上作用力在x、y方向的分量为：

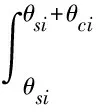
(16)

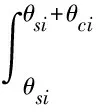
(17)

R2为管片外半径。

管片上作用力对管片中心的力矩为：

(18)

di2为管片中心点到管片上点与圆心的连线。在每一个时间单元dt内对整个管片进行一次空间上的积分，得到该时刻作用在管片上的合力，最后通过编程计算得到每块管片在各种工况下的径向合力、切向合力及对各管片中心力矩的时程曲线。

3.2 控制方程的建立与求解

综合管片位移几何关系和接头受力关系，可得管片在x,y方向的平动及转动微分方程为：

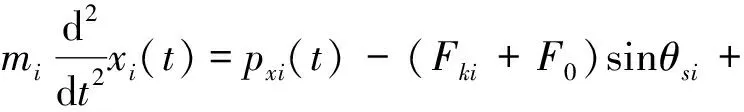
(Fki+1+F0)sin(θsi+θci)+(fi+Gi)cosθsi+

(fi+1+Gi+1)cos(θsi+θci)

(19)

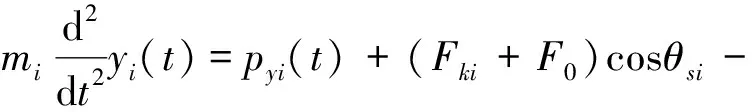
(Fki+1+F0)cos(θsi+θci)+(fi+Qi)sinθsi+

(fi+1+Qi+1)sin(θsi+θci)

(20)

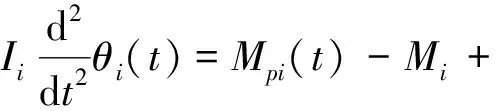
Mi+1-(Fki-Fki+1)R0

(21)

式中，mi、Ii分别是第i管片的质量和绕管片外弧中心的转动惯量，xi(t)、yi(t)、θi(t)分别为管片在x，y方向的位移函数及转动的角位移函数。

根据管片在静力状态下的方程求解出管片的初始状态，再用龙格—库塔法求解(19)～(21)微分方程组，可求得管片结构在爆炸荷载下的位移和内力。

4 算例及分析

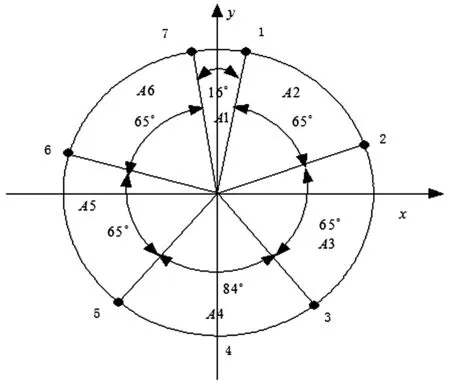
图5 管片横向接头示意图

以南京地铁为研究对象，管片接头布置如图5所示，隧道衬砌外径为6.2 m，管片厚度为0.35 m，管片宽度为1.2 m。采用C50钢筋混凝土管片，衬砌材料密度为2.5 t/m3，泊松比为0.2，弹性模量为3.45×104N/mm2。管片接头刚度采用kθ=3.45×107N·m/rad,环向接头刚度为kn=3.93×1010N/m,接头刚度模型法采用双直线接头刚度模型。隧道埋深为14 m，在隧道衬砌正上方6 m处设置TNT炸药，炸药当量为5 kg，土层的动力计算参数如表1所示。

表1 土层参数表

4.1 方法验证

为了验证方法的正确性，将本文计算结果与通用有限元软件LS-DYNA计算结果进行对比，管片采用壳单元模拟，用接头单元来模拟管片接头效应，考虑了管片与螺栓之间、管片与管片之间、管片与土体之间的相互作用，围岩采用Drucker-Prager屈服条件。

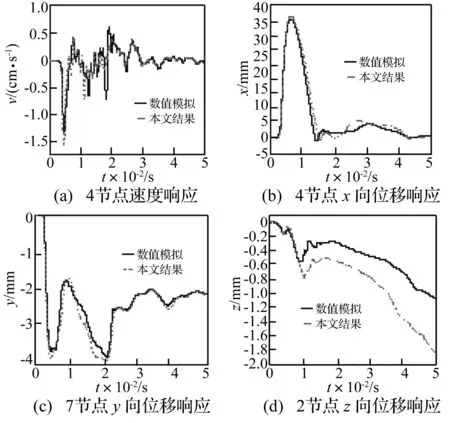
图6 两种方法求解的比较

管片上不同节点响应数值模拟计算结果和简化计算方法对比结果见图6。从图中可以看出，简化计算的速度时程曲线和位移时程曲线与数值计算的变化规律基本一致，采用简化计算方法算出的速度偏大，位移偏小。引起偏差的原因：一方面是爆炸荷载作用下管片结构会产生弯曲变形，而简化计算中将管片简化为刚体，忽略管片自身的变形，只考虑单个管片的运动；另一方面是没有考虑荷载作用下管片材料自身的变形。

4.2 管片厚度的影响

分别采用4种管片厚度：200 mm、300 mm、400 mm、500 mm，管片外直径取6.2 m，其它参数不变。图7为管片厚度对拱顶位移和弯矩的影响。可以看出：管片厚度越大，拱顶位移和弯矩越大，相应峰值滞后，振动频率减小，尤以弯矩的变化最为显著，此外，增加相同的厚度，厚度大的时候，位移和弯矩增加的相对小一些，可见随着厚度的增加它们的变化趋势趋向于平缓状态。这表明管片厚度的增大对爆炸荷载作用下隧道管片的受力是不利的，这与日本学者冈本舜三的调查结果是一致的。衬砌的刚度与管片厚度的三次方成正比，厚度的改变直接改变了衬砌的整体刚度，以及衬砌与周围地层的刚度比，从而在地层参数不变的情况下改变管片环的受力情况。管片厚度是盾构法隧道设计中的一项重要参数，其取值大小不仅影响隧道的造价，而且还直接影响隧道受力及使用性能。厚度降低，可以节约材料、减小开挖量，降低工程造价，因此在确定管片厚度时应尽可能在满足结构承载力的前提下取规范的最小值。

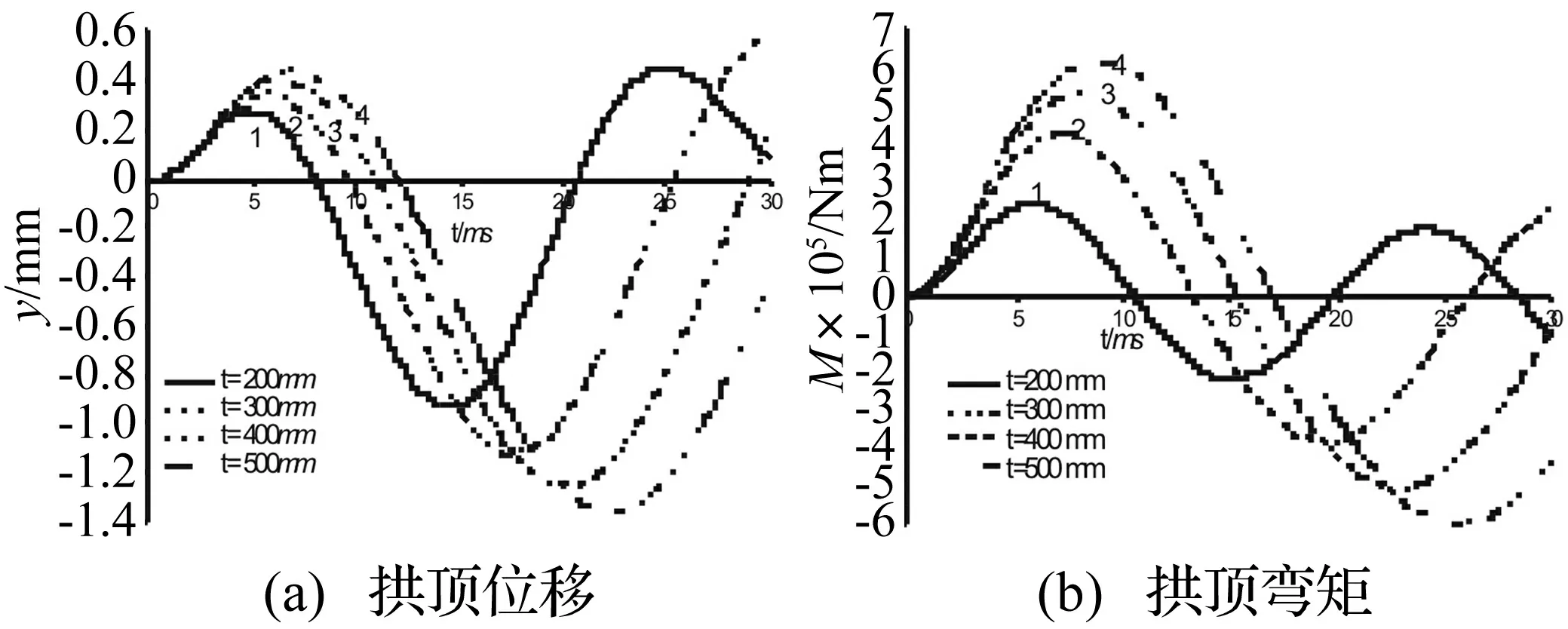
图7 管片厚度的影响

4.3 管片直径的影响

直径也是衬砌基本几何参数之一。分别采用3种管片直径：6 m、8 m、10 m，管片厚度取0.35 m，其它参数不变。图8为管片直径对拱顶位移和弯矩的影响。可以看出：拱顶位移和弯矩的响应随管片直径的增大而增大，尤以弯矩的变化最为显著，此外，管片直径越大，位移和弯矩增加的越小，可见随着直径的增加它们的变化趋势趋向于平缓状态。

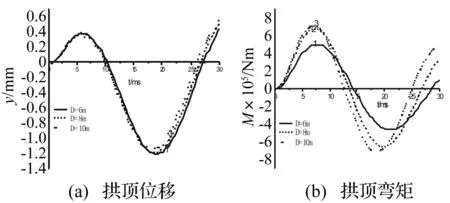
图8 管片直径的影响

5 结 论

针对地铁区间隧道面临的恐怖爆炸威胁，对爆炸荷载作用下地铁管片结构的动力响应问题进行了研究，主要结论有：

(1) 忽略管片的变形，将盾构隧道衬砌结构看作由弹塑性铰链连接的刚性管片组成，考虑土与结构的相互作用，提出了一种爆炸荷载作用下管片结构动力分析的简化计算方法。

(2) 通过算例对比，本文的简化计算方法与数值计算结果较为一致，而且本文方法简单实用。

(3) 管片厚度的变化对衬砌动力响应的影响显著，管片厚度越大，结构的内力反应越大。管片直径的增加使位移和弯矩峰值增大，但变化并不明显。改变管片厚度和管片直径等管片结构参数可以改变管片环的刚度，从而在地层参数不变的情况下改变管片环的受力情况，因此在设计中应该选取适当的厚度和直径。

爆炸荷载作用下管片结构会产生弯曲变形，同时强冲击荷载作用下管片材料自身也会产生变形，这些问题有待进一步研究。

参 考 文 献

[1]孔德森,孟庆辉,张伟伟,等.爆炸荷载作用下地铁隧道的冲击反应研究[J].振动与冲击,2012,31(12):68-72.

KONG De-sen, MENG Qing-hui, ZHANG Wei-wei, et al. Shock responses of a metro tunnel subjected to explosive loads [J]. Journal of Vibration and Shock, 2012,31(12):68-72.

[2]刘齐建,赵跃宇.径向谐和激励下圆形隧道衬砌的动力稳定性[J].湖南大学学报(自然科学版),2011,38(9):22-26.

LIU Qi-jian, ZHAO Yue-yu. Dynamic stability of circular tunnel linings subjected to radial harmonic excitation [J]. Journal of Hunan University(Natural Science),2011,38(9):22-26.

[3]刘沐宇,卢志芳.接触爆炸荷载下长江隧道的动力响应分析[J].武汉理工大学学报,2007,29(1):113-117.

LIU Mu-yu, LU Zhi-fang. Analysis of dynamic response of Yangtze River tunnel subjected to contact explosion loading[J]. Journal of Wuhan University of Technology, 2007,29(1):113-117.

[4]马立秋,张建民,张 嘎,等.爆炸离心模型试验系统研究与初步试验[J].岩土力学,2011,32(3),946-950.

MA Li-qiu, ZHANG Jian-min, ZHANG ga, et al. Research of blasting centrifugal modeling system and basic experiment [J]. Rock and Soil Mechanics,2011,32(3),946-950.

[5]马立秋,张建民,胡 耘,等.地面爆炸条件下浅埋地下结构响应的离心模型试验研究[J].岩石力学与工程学报,2010,29(z2):3672-3678.

MA Liqiu, ZHANG Jian-min, HU Yun,et al. Centrifugal model tests for responses of shallow-buried underground structures under surface blasting [J]. Chinese Journal of Rock Mechanics And Engineering,2010,29(z2):3672-3678.

[6]刘干斌,郑荣跃,周 晔.爆炸荷载作用下软土隧道动力响应数值模拟[J].宁波大学学报(理工版),2009,22(2):263-267.

LIU Gan-bin, ZHENG Rong-yue, ZHOU Ye. Numerical model for dynamic response of tunnel in clay [J]. Journal of Ningbo University (Natural Science & Engineering Edition),2009,22(2):263-267.

[7]Karinski Y S, Yankelevsky D Z. Dynamic analysis of an elastic-plastic multisegment lining buried in soil [J]. Engineering Structures, 2007,29(1):317-328.

[8]罗昆升,赵跃堂,罗中兴,等.地铁盾构隧道管片结构初始状态的数值模拟分析[J].土木工程学报,2013,46(4):78-84.

LUO Kun-sheng, ZHAO Yue-tang, LUO Zhong-xing, et al. Numerical simulation on initial stress and strain state of subway segmented tunnel[J]. China Civil Engineering Journal ,2013,46(4):78-84.

[9]罗昆升,王 勇,赵跃堂,等.地铁区间隧道在店面爆炸荷载作用下的数值模拟[J].解放军理工大学学报(自然科学版),2007,8(6):674-679.

LUO Kun-sheng, WANG Yong, ZHAO Yue-tang, et. Numerical simulation of section subway tunnel under surface explosion [J]. Journal of PLA University of Science and Technology , 2007,8(6):674-679.

[10]王 苏,路得春,杜修力.地下结构地震破坏静-动力耦合模拟研究[J].岩土力学,2012,33(11):64-69.

WANG Su, LU De-chun, DU Xiu-li. Research on underground structure seismic damage using static-dynamic coupling simulation method [J]. Rock and Soil Mechanics,2012,33(11):64-69.

[11]TM5-855-1. Fundamentals of protective design for conventional weapons[S]. Vicksburg: US army engineers waterways experimental station, 1986.

[12]B.A.柯略列夫斯基,B.и.加努希金,A.A.柯斯金.民防掩蔽部[M].南京：中国人民解放军工程兵工程学院,1989.

[13]朱 伟,钟小春,秦建设.盾构隧道管片接头力学分析及双直线模型研究[J].岩土力学,2006,27(12):2155-2158.

ZHU Wei, ZHONG Xiao-chun, QIN Jian-she. Mechanical analysis of segment joint of shield tunnel and research on bilinear joint stiffness model [J]. Rock and Soil Mechanics,2006,27(12):2155-2158.