基于气流激振的离心式压缩机管道破坏机理研究

李宏坤， 郭 骋， 张晓雯， 赵鹏仕， 张学峰

(大连理工大学 机械工程学院，大连 116024)

大型压缩机组是关系国民经济的关键设备，管道是保证石化企业生产的重要传输途径。随着压缩机朝着大型化、高速化的发展，压缩机组管道振动的问题越发频繁。管道振动会造成管道结构的疲劳破坏，管道连接件松脱，引起管道泄漏以及严重的事故。如何降低管道疲劳破坏，具有很高的理论研究价值和重大的现实意义。对管道振动的研究，引起众多学者的广泛关注。Norton[1]提出了工程中的管道振动问题，Fahy[2]对管道的振动问题进行了进一步研究，Eisinger[3-5]对管道内部声模态引起的声疲劳现象进行了深入研究。管道及其支架连同与之相连的设备构成了一个复杂的机械系统，在有激振力的情况下，这个系统就会产生振动。管道振动的原因主要归结为：①动力平衡性差，机械结构不平衡及基础结构设计不合理引起的振动。通常情况下，管路和机组连接在一起运行，如果机组的动力平衡不满足设计要求，或者在安装时出现偏差，以及转子在长时间运行后，由于腐蚀，磨损，零件损坏，造成机组结构的不平衡，就会造成管道振动[6-8]。通过增加支承，改变支承位置等方式可以改变管道系统的刚度矩阵[9]，进而减小管道振动。②在压缩机组的运行过程中，由于叶轮的高速旋转，使得流体形成压力脉动，压力脉动是引起管道上振动的重要因素[10-11]。作为管道振动的主要激励源，降低压力脉动对应频率的幅值可以有效降低管道振动。本文研究基于声共振对管道内流体压力脉动的影响，分析在气流激振作用下的动态特性，进而研究有效抑制气流激振下管道疲劳破坏的方法。

1 声模态

声模态是空气介质的特有属性，声模态表现为空气在其固有频率下声压的振动分布情况。声模态主要与空腔结构的形状、位置特性等参数有关。可以通过声学有限元的方法计算获得结构空腔声模态的特征参数。当激励频率与管道空腔的声模态频率相近时，管道中的空气介质会产生共振现象，增大气流的脉动幅值和压力不均匀度。在设备运行过程中，由声模态引起的气流激振反复作用于管道，最终会导致管道的疲劳破坏。在声学理论中,亥姆霍兹方程(Helmholtz Equation)作为基本方程之一，对声学计算起指导作用。

2p(x,y,z)-k2p(z,y,z)=-jρ0ωq(x,y,z)

(1)

式中：k为波数，k=ω/c=2πf/c，ω为角频率，ω=2πf，对应的波长为λ=2π/k=c/f。

对于上式所表达的亥姆霍兹方程，可以通过利用声学有限元法获得其解。在线性空间中，任意一个声压分布向量均可以由一组线性无关的声压向量线性地表示出来。线性无关的声压向量通常取特征值向量，即声学模态[12]。声学模态是声学质量矩阵和声学刚度矩阵的特征值，即:

(Ka-ω2Ma){φ}={0}

(2)

任意一个声压向量{pi}可以由n个特征值{φi}线性地表示出来，即:

{Pi}=λ1{φ1}+λ2{φ2}+…+λn{φn}=φ{λ}

(3)

式中：φ=[φ1φ2…φn]称为模态矩阵，{λ}=[λ1λ2…λn]T称为模态参与因子[13]。

将式(3)代入式(2)得:

[Ka]+jω[Ca]-ω2[Mα]·φ{λ}={Fai}

(4)

在上式的两边同时乘以模态矩阵φT得:

φTKaφ+jωφTCaφ-ω2φTMaφ{λ}=φT{Fai}

(5)

2 声模态仿真计算与试验验证

为了对气流激振产生的机理进行有效分析，本文对大连理工大学能源与动力学院叶轮流体机械研究所实验室的流体机械设备管道进行分析。管道除去双扭线出口部分的总长为2 866 mm，内径为400 mm，外径为412 mm，管道底部通过钢架支座与地面固定连接。管道中部安放有一个由变频电机控制的具有6个叶片的风机，管道模型，传感器布置图及二维图分别见图1至图3。管道内的主要激励频率，即叶片通过频率为：

(6)

式中:f为激励频率(叶片通过频率)Hz；n为电机转速，转/分；m为叶片数。

图1 管道实物模型

图2 传感器布置图

图3 管道二维模型图

2.1 仿真计算

采用Solidworks软件按照管道内部空腔直径400 mm，长度2 866 mm，进行三维建模。采用高阶20节点的六面体Solid186单元对空腔模型进行全六面体网格划分，在网格划分时，根据声速和单元尺寸可以确定计算所得最大频率。为了保证声学单元在每个波长范围内最少有6个单元，有限元单元长度取0.05 m，声学计算结果的最高频率可达6 300 Hz，充分满足了计算要求。采用ANSYS软件网格划分离散后的有限元结构共得到12512个节点，28512个单元。如图4所示。

图4 管道空腔有限元网格模型

将有限元网格模型导入LMS Acoustic模块采用声学有限元模块进行分析，定义声速为v=340 m/s，流体介质的密度为ρ=1.225 kg/m3。通过声学前处理操作，形成的声学包络网格，如图5所示。LMS Acoustic模块将要计算的声场离散成一定数量的小声场，每个小声场即处理后每一个小的声学单元，所有离散后的单元转换构成了用于声学有限元计算的质量、阻尼、刚度矩阵。声学单元之间通过节点首尾相连，每个单元内的声场由属于这个单元的节点上的声压与单元之间的相关形函数确定。声学有限元通过调用特定求解器，即可计算得出特征值，随后根据形函数，将计算结果传递转换给每个单元。即可得出声模态的固有频率和声压振动分布情况。

图5 管道空腔声学包络网格模型

在实际现场，管道的入口和出口直接连着大气，声音通过出、入口直接传播到大气中。声学包络网格仅模拟的是全反射的环境，而实际情况声波会通过出、入口向外界传播。所以要对声学包络网格定义两端的阻抗属性，声阻抗是流体介质的一个重要参数，可表示为声波波振面某一面积上的声压与通过这个面积的质点速度的比值。在包络网格两端对材料添加空气声阻抗，以模拟管道空腔两端的全吸声边界。采用Block Lanczos方法(兰索斯法)将声学的对称矩阵通过正交相似变换为对称矩阵，计算管道空腔的声模态，得到前10阶的固有频率和共振时的声压分布。

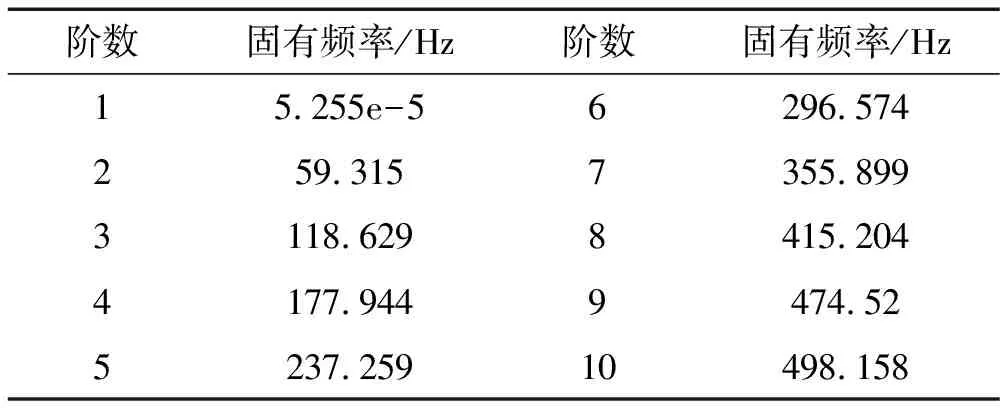
表1 管道空腔的声模态

第一阶固有频率时的声压分布为静态声压时的情况，相当于结构模态计算时的刚体模态，可以忽略不计。前二至五阶固有频率时的声压分布见图6(a)-图6(d)。

2.2 实验测试

为了验证空腔结构是否在固有频率处发生共振现象，采用杭州亿恒AVANT数据采集与分析系统对管道利用声压传感器以及加速度传感器对空腔的声压信号和管壁的振动信号进行测试分析。测试所采用声压传感器的灵敏度为40mv/pa，加速度传感器的灵敏度为96.49mv/g。测试采样点数为32768，采样频率为10 240 Hz。

图6 声压分布

在管道孔壁上安装声压传感器，测量管道空腔声压值的变化。在相同位置的壁面吸附加速度传感器以采集振动信号。由于电机转速范围有限，测试时的采取调速范围从450-3000 r/min，连续升速的方法进行声、振信号的测试分析。从测试的时域波形图7中可以看出在波形幅值存在明显的波动部分。对测试所得时域波形进行频谱分析，当频谱波形的特征频率与仿真计算的固有频率相近时，其所对应的频域波形会出现大幅度的波动。

为了对空腔计算结果进行进一步的验证，采取对电机划分为520-590 r/min、1100-1200 r/min、1700-1800 r/min、2300-2400 r/min这四段转速范围，按照缓慢、平稳升速的方法，对管道内部空腔的声压值和管壁加速度幅值的变化进行测试分析。对结果进行频谱分析，声压频谱幅值在电机转速为580 r/min，1170 r/min，1760 r/min，2363 r/min，即激励频率为58、117、176、236 Hz时出现幅值波动，以一段转速范围为例，电机转速为520-590转/分时的管道内部声压幅值变化见图8，频率分布与仿真模拟结果近似，在激励频率为58Hz时，频谱声压结果出现最大值。电机转速为520-590转/分时的管壁振动幅值变化见图9，与空腔声压测试结果出现相同的情况，在电机转速为580rpm时出现幅值激增的现象。117，176与236 Hz也有相同的测试结果，分析表明理论仿真与实际测试具有较好的吻合。

图7 管道空腔的声压时域波形

图8 转速为520-590转/分时声压幅值变化

图9 电机转速为520-590转/分时振动幅值变化

通过比较仿真结果与试验测试所得空腔的固有频率相差不到3%。仿真计算结果与实际测试基本一致，证明了仿真计算的可靠性。激励频率与空腔声模态固有频率相近时，频谱声压幅值比其它频率时的幅值有明显的增大，管道壁面振动加强，气流激振作用加强，管道内部的空腔出现声共振现象。

表2 管道固有频率

根据管道的实际情况，对管道支撑部分进行位移全约束。对管道模态计算结果如表2所示，可以得出实验中管道内气流脉动增大现象与管道固有频率无关，但与声模态的频率密切相关。为了减小管道在运行过程中由于激振频率与声模态频率相近而引起流体介质气流激振，可以在设计阶段改进设备结构，以达到改变空腔固有频率的目的，从而使这些激振频率与管道声模态频率之间留存较大的幅值裕度，降低气流激振幅度，以免引起管道产生高频振动，进而造成疲劳破坏。

3 压缩机管道改进设计

某离心式空气压缩机管道因为振动剧烈造成多次破裂，该离心式压缩机中由16个叶片的叶轮运转，其转速为6 300 r/min，在加固管道结构后，情况并没有改善，管道修补后的情况见图10。

通过对压缩机及管道的现场测试，与传统的低频振动相比，此次压缩机组主要为高频振动，并且与气流的通过频率相一致，也就是转频×叶片数。如图11(a)所示。此主要表现为气流激励下的高频振动，也就是一种强迫振动，而振动来源就是气流激励。

为此，从气流激振产生的激励进行分析，从声场与流场的耦合作用入手，分析管道高频破坏原因，可以得出管道振动主要是因为叶轮激振频率与空腔声模态频率相近，从而产生了较大强度的气流激振，进而使管道产生疲劳破坏。并在此基础上， 进行气流激振产生机理溯源，从压缩机结构进行改进方案研究，改变了系统的声模态，避免了气流激振的产生，从根本上抑制了气流激振的产生，有效抑制了管道的振动。改进后的管道振动频谱如图11(b)所示，其明显降低，满足工程实际要求。由于篇幅的限制，这里不做详细介绍。

图10 修补后的管道

4 结 论

本文研究管道振动与声共振之间的关系，研究了气流激振对管道疲劳破坏的作用机理，当激励频率与声模态固有频率相近时，空气介质产生声共振现象，使得管道内的压力脉动增大，管道振动增强，即气流激振作用增大，空腔声压和管道振动幅值急剧变化。从而导致压力脉动幅值和不平均度增大，由于管道刚度不能抵御强烈的气流激振，故而造成疲劳破坏失效。本文的研究为预防管道高频振动的产生提供了借鉴意义。

参 考 文 献

[1]Norton M P. Fundamentals of noise and vibration analysis for engineers[M]. Cambridge University Press, Cambridge, U.K. 1989.

[2]Fahy F J, Sound and structural vibration[M]. Academic press, London, New York.1998.

[3]Eisinger F L. Designing piping systems against acoustically induced structural fatigue[J]. Journal of Pressure Vessel Technology,1997,119(3): 379-383.

[4]Eisinger F L, Francis J T, Acoustically induced structural fatigue of piping systems[J]. Journal of Pressure Vessel Technology,1999,121(4):438-443.

[5]Eisinger F L, Sullivan R E, Acoustic vibration in a stack induced by pipe bends[J]. Journal of Pressure Vessel Technology,2003,125:228-232.

[6]陈海峰.往复压缩机管道振动特性及安全评定研究[D].中国石油大学，2009.

[7]任建亭,姜节胜.输流管道系统振动研究进展[J].力学进展，2003,33(3),313-324.

REN Jian-ting, JIANG Jie-sheng. Advances and trends on vibration of pipes conveying fluid[J].Advances in Mechanics, 2003,33(3):313-324.

[8]王乐勤,何秋良.管道系统振动分析与工程应用[J].流体机械，2002,30(10):28-42.

WANG Le-qin, HE Qiu-liang. Reciprocating compressor pipeline vibration and engineering application[J]. Fluid Machinery, 2002, 30(10):28-32.

[9]赵力电.压力管道振动分析[J].管道技术与设备，2006,6,31-32.

ZHAO Li-dian. Analysis of pressure pipeline vibration causes[J]. Pipeline Technique and Equipment, 2002,6:31-32.

[10]李 鹤,杨铎,闻邦椿,等.大型压缩机管道系统振动现场测试与控制[J].振动与冲击,2007,26(4):158-160.

LI He, YANG Duo, WEN Bang-chun, et al. Vibration measurement and control of a large scale compressor-pipeline system[J].Journal of Vibration and Shock,2007,26(4):158-160.

[11]税朗泉,刘永寿,顾致平,等.轴向周期激励下含脉动流体的简支管道横向振动的稳定性分析[J].振动与冲击,2012,31(7):133-136,141.

SHUI Lang-quan,LIU Yong-shou,GU Zhi-ping,et al.Stability of transverse vibration for a pinned-pinned pipe conveying pulsing fluid under axial periodic excitation[J].Journal of Vibration adn Shock,2012,31(7):133-136,141.

[12]付东旭.车内振动噪声分析与优化控制技术的研究[D].合肥:合肥工业大学，2011.

[13]李增刚,詹福良.Virtual.Lab声学仿真计算高级应用实例[M].北京：国防工业出版社，2010.