圈的无重复分数染色

朱绪鼎， 钟亚玲

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

如果一个偶长度的序列x1x2…x2l的前一半和后一半是一样的,即对任意的1≤i≤l,xi=xi+l,那么就称该序列为一个重复.如果一个序列不含有重复的子序列,那么就称该序列为一个无重复的序列.1906年，Thue[1]证明了仅用3个符号可以写出一个无限长的无重复序列.Thue的这个结果在数学的很多分支中有重要的影响,它催生了一个新的学科：符号动力学.Thue定理及其推广在数学和计算机科学的不同领域中有许多重要的应用.

2002年，Alon等[2]将无重复序列的概念和图的染色结合起来,提出了图的无重复染色的概念.图G的一个顶点染色c是无重复的是指图G中的任何一条简单路v1v2…v2l的颜色序列c(v1)c(v2)…c(v2l)不是一个重复.称一个无重复染色所需要的最少颜色数为图G的Thue染色数，记为π(G),即

π(G)=min{n:图G存在一个无重复的n-染色}.

根据π(G) 的定义,Thue的结果等价于π(P∞)=3.

图的无重复染色数在文献[2-6]中已有大量的研究,得到了许多类图的无重复染色数的上下界.特别是在文献[4]中,Currie确定了所有圈图的无重复染色数.

定理1[4]设Cn是顶点数n≥3的圈图.若n=5,7,9,10,14,17,则π(Cn)=4;否则π(Cn)=3.

下面给出图G的无重复分数染色的定义.

根据πf(G)的定义,对任意的图G,πf(G)≤π(G).一个很自然的问题是:哪些图G满足πf(G)=π(G)?如果πf(G)≠π(G),那么π(G)-πf(G)的差值有多大?笔者已另文(待发表)证明了,若图G是一条路或者是一棵没有2度点的树,则πf(G)=π(G)；同时还构造了一个树图T,它的无重复分数染色数是3.5,而它的无重复染色数是 4；对于圈图的无重复分数染色数,得出除了n=10,14,17之外的所有n的πf(Cn)值.

对于圈图Cn(n=10,14,17),πf(Cn)的研究更加困难.本文研究了这3个圈的无重复分数染色数的上下界.

图1 圈C10的一个无重复的2-重7-染色

1 圈C10

性质1 若Y是X-rich,Z 是Y-rich,则X∩Z≠Ø;若XYZ∈T,YZW∈T,则W 是X-rich.

在接下来的讨论中,若XYZ∈T,并且YZW∈T,则记XYZW∈Q.通过性质1,若XYZW∈Q,则W是X-rich.

引理1 令P=(v1v2v3v4)是一条含有4个顶点的路.若c是P的一个无重复的k-重n-染色,则c(v1)∩c(v3)=Ø,或者c(v2)∩c(v4)=Ø.

引理2 假设P6=(v1v2…v6)是圈C10的一条路.若X1X2X3∈T,并且X4X5X6∈T, 则

1)X4,X5,X6分别是X2,X1,X3-rich;或者

2)X4,X5,X6分别是X1,X3,X2-rich.

情形1 X4∩X1=Ø.即X2X1X3X4∈Q,由此可以推导出X4是X2-rich.由X4∩X2≠Ø,通过引理1就能推导出X5∩X3= Ø.现在可以根据X1X3X4X5∈Q, 推导出X5是X1-rich.根据X3X4X5X6∈Q, 推导出X6是X3-rich.故1)成立.

情形2 X4∩X2=Ø.因此,X1X2X3X4∈Q,可得X4是X1-rich.若X5∩X2= Ø,则可由X2X4X5X6∈Q推导得到X6是X2-rich.同理,X3X2X4X5∈Q,推导得到X5是X3-rich.若X5∩X2≠Ø,则X6∩X3=Ø.否则,令a∈X1∩X4,b∈X2∩X5,c∈X3∩X6,在路v1v2v3v4v5v6上可以找到形如abcabc的一个重复.因此,由X2X3X4X6∈Q推导出X6是X2-rich;由X3X4X6X5∈Q推导出X5是X3-rich.综上所述,得2)成立.

情形3 X4∩X1≠Ø,X4∩X2≠Ø.由引理1知,X5∩X3= Ø.因此,可以根据X3X4X5X6∈Q推导出X6是X3-rich.这样就有X5∩X2=Ø.否则,令a∈X1∩X4,b∈X2∩X5,c∈X3∩X6,可以在路v1v2v3v4v5v6上找到形如abcabc 的一个重复.此时就可以根据X1X2X3X5∈Q推导出X5是X1-rich,同时由X2X3X5X4∈Q推导出X4是X2-rich.因此，1)成立.引理2证毕.

引理3 不可能有X1X2X3∈T, X4X5X6∈T, X7X8X9∈T.

证明 反正法.假设X1X2X3∈T, X4X5X6∈T, X7X8X9∈T. 根据引理2和对称性,对于颜色序列X1X2X3X4X5X6,可以假设X4,X5,X6分别是X2,X1,X3-rich.

同样,对于颜色序列X4X5X6X7X8X9,应用引理2.若引理2的1)成立,即X7,X8,X9分别是X5,X4,X6-rich,则X7∩X1≠Ø(因为X7和X1都是X5-rich).同理,X8∩X2≠Ø,X9∩X3≠Ø.接下来证明

X10∩X4=Ø,X10∩X6=Ø.

若不然,则令a∈X1∩X7,b∈X2∩X8,c∈X3∩X9,d∈X10∩X4,或者a∈X1∩X7,b∈X2∩X8,c∈X3∩X9,d∈X10∩X6.因此，可在路v7v8v9v10v1v2v3v4上找到形如abcdabcd的一个重复,或者可在路v6v7v8v9v10v1v2v3上找到形如dabcdabc的一个重复.

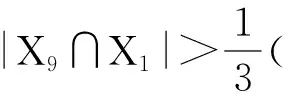
推论1 若X1X2X3∈T, 且X4∩X6≠Ø,则X2∩X4≠Ø.

证明 反正法.假设X2∩X4=Ø,则X2X3X4∈T, X5X6X7∈T. 根据引理3得X8∩X10≠Ø,X9∩X1≠Ø,故可令a∈X8∩X10,b∈X9∩X1,从而可以在路v8v9v10v1上找到形如abab的一个无重复.得到矛盾.推论1证毕.

引理4 存在一个整数i,使得对j=0,1,2,3,4,Xi+2j∩Xi+2j+2≠Ø.这里的下标运算是模10 加法.

证明 设i∈{1,2,…,10},令Ti=max{k:Xi+2j∩Xi+2j+2≠Ø, j=1,2,…,k}.这里的下标运算是模10 加法.显然,对任意的i,Ti≤4.令T=max{Ti:1≤i≤4}.

若T=0,不妨设T1=T=0,则X1∩X3≠Ø,X3∩X5=Ø,X9∩X1=Ø.同时由引理1知,X2∩X4=Ø.那么就有X10X1X2∈T, X3X4X5∈T, 通过引理3得,X6∩X8≠Ø.由引理1得,X5∩X7=Ø.故X2X3X4∈T,X5X6X7∈T.同样,根据引理3,有X8∩X10≠Ø,即与T=0矛盾.

若T=1,不妨设T1=T=1,则X1∩X3≠Ø,X3∩X5≠Ø,X5∩X7=Ø,X9∩X1=Ø.那么就有X9X10X1∈T, X2X3X4∈T, X5X6X7∈T, 与引理3矛盾.

若T=2,不妨设T1=T=2,则X1∩X3≠Ø,X3∩X5≠Ø,X5∩X7≠Ø,X7∩X9=Ø.那么就有X4X5X6∈T,X7X8X9∈T,根据引理3,就有X10∩X2≠Ø.此时可令a∈X10∩X2,b∈X1∩X3,则在路v10v1v2v3上存在形如abab的一个重复.矛盾.

若T=3,不妨设T1=T=3,则X1∩X3≠Ø,X3∩X5≠Ø,X5∩X7≠Ø,X7∩X9≠Ø,X9∩X1=Ø.那么就有X6X7X8∈T, X9X10X1∈T, 根据引理3,有X2∩X4≠Ø.此时可令a∈X2∩X4,b∈X3∩X5,则在路v2v3v4v5上存在形如abab的一个重复.矛盾.

综上可得T=4.引理4证毕.

在以下的讨论中,不妨假设X1∩X3,X3∩X5,X5∩X7,X7∩X9,X9∩X1都是非空的.根据引理1得,X2X3X4,X4X5X6,X6X7X8,X8X9X10,X10X1X2∈T.

引理5 对任意的i,若Xi∩Xi+3=Ø,则Xi∩Xi-3≠Ø.

证明 根据i的奇偶性,分2种情形讨论.

情形1 i是偶数.根据对称性,不妨设i=6.假设X6∩X3=Ø,且X6∩X9=Ø.因此,X2X3X4X6∈Q⟹X6是X2-rich,X10X8X9X6∈Q⟹X6是X10-rich.则X10∩X2≠Ø.故可令a∈X10∩X2,b∈X1∩X3,从而在路v10v1v2v3上存在形如abab的一个重复.矛盾.

情形2 i是奇数.根据对称性,不妨设i=3.假设X3∩X6=Ø,且X3∩X10=Ø.因此,X4X2X3X10∈Q⟹X10是X4-rich,X1X2X10X3∈Q⟹X3是X1-rich,X5X4X6X3∈Q⟹X3是X5-rich,X2X3X4X6∈Q⟹X6是X2-rich.

若X3∩X9≠Ø,则可令a∈X9∩X3,b∈X10∩X4,c∈X1∩X5,d∈X2∩X6.因此,在路v9v10v1v2v3v4v5v6上存在形如abcdabcd的一个重复.所以X3∩X9=Ø.

若X3∩X7≠Ø,则可令a∈X3∩X7,b∈X10∩X4,c∈X1∩X5,d∈X2∩X6.因此,在路v10v1v2v3v4v5v6v7上存在形如bcdabcda的一个重复.所以X3∩X7=Ø.

综上可得X8X9X10X3∈Q, 所以X3是X8-rich.

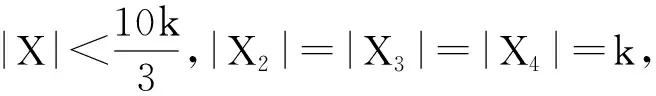
则

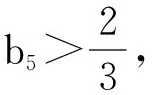
综上所述,X1,X5,X8都是X3-rich,X10和X7都是X4-rich,X6和X9都是X2-rich,这样可以推导出X10∩X7,X9∩X6,X8∩X5都非空.

现令a∈X10∩X7,b∈X9∩X6,c∈X8∩X5,在路v10v9v8v7v6v5上存在形如abcabc的一个重复.矛盾.引理5证毕.

引理6 不存在i,使得Xi∩Xi+3≠Ø,且Xi+1∩Xi+4≠Ø.

证明 假设存在i,不妨设i=1,使得X1∩X4≠Ø,且X2∩X5≠Ø.接下来证明X10∩X3=Ø,且X3∩X6=Ø.若不然,令a∈X10∩X3,b∈X1∩X4,c∈X2∩X5,或者令a∈X1∩X4,b∈X2∩X5,c∈X3∩X6.则在路v10v1v2v3v4v5上存在形如abcabc的一个重复,或者在路v1v2v3v4v5v6上存在形如abcabc的一个重复.矛盾.故存在i,使得Xi∩Xi-3=Ø,且Xi∩Xi+3=Ø.与引理5矛盾.引理6证毕.

引理7 不存在i,使得Xi∩Xi+3=Ø,且Xi+1∩Xi+4=Ø.

证明 假设存在i,使得Xi∩Xi+3=Ø,且Xi+1∩Xi+4=Ø.根据引理5,Xi∩Xi-3≠Ø,Xi+1∩Xi-2≠Ø,与引理6矛盾.引理7证毕.

由引理6和引理7,可再分2种情形进行讨论.

情形1 设X1∩X4,X3∩X6,X5∩X8,X7∩X10,X9∩X2都非空,则X2∩X5,X4∩X7,X6∩X9,X8∩X1,X10∩X3都是空集.这样推导出X2X4X5X6,X4X6X7X8,X3X2X4X5,X5X4X6X7,X7X6X8X9∈Q ,则X2∩X6,X3∩X7,X4∩X8,X5∩X9都非空.令a∈X2∩X6,b∈X3∩X7,c∈X4∩X8,d∈X5∩X9,则在路v2v3v4v5v6v7v8v9上存在形如abcdabcd 的一个重复.矛盾.

情形2 设X1∩X4,X3∩X6,X5∩X8,X7∩X10,X9∩X2都是空集,则X2∩X5,X4∩X7,X6∩X9,X8∩X1,X10∩X3都是非空.这样就推导出X10X2X1X4∈Q,X4X5X6X8∈Q,即X10和X8都是X4-rich,也就是X10∩X8≠Ø.令a∈X8∩X10,b∈X9∩ X1,则在路v8v9v10v1上存在形如abab的一个重复.矛盾.定理2证毕.

2 圈C14,C17

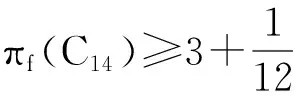
随着圈的长度增加,研究难度更大,笔者将采取另外的方法进行研究.

下面以X3,X4,X5,R 为参照,描述其他的颜色集Xj.令

Xj=(aj,bj,cj,rj)k,j=1,2,…,n,

则

aj≤1,bj≤1,cj≤1,rj≤ε,且aj+bj+cj+rj=1.

引理8 设P8=v1,v2,…,v8.若X3X4X5∈T, 则a6>ε和b6>ε不可能同时成立.

证明 反正法.假设a6>ε,b6>ε同时成立.因为相邻的颜色集不相交,所以X6∩X5=Ø,即根据前面的描述有c6=0.因为b6>ε,所以X6∩X4≠Ø.根据引理1,就有X7∩X5=Ø,即c7=0.

接下来证明a7>0,b7>0.因为r7≤ε,a7+b7+c7+r7=1,所以a7,b7不可能同时为零.

假设a7=0,则 b7=1-a7-c7-r7≥1-ε.因为b6+b7>1,所以X6∩X7≠Ø.矛盾.从而a7>0.同理可证b7>0.所以a7>0,b7>0.

下面证明c8=0,c2=0.若不然,则令a∈X3∩X6,b∈X4∩X7,c∈X5∩X8.因此,在路v3v4v5v6v7v8上就可找到一个重复abcabc;或者令a∈X3∩X6,b∈X4∩X7,c∈X5∩X2,在路v2v3v4v5v6v7上同样可以找到一个重复cabcab.

因为X3∩X2= Ø,所以a2=0.通过计算得b2=1-a2-c2-r2=1-r2≥1-ε.此时X2∩X4≠Ø,b2+b6>1.根据引理1,X1∩X3=Ø,即a1=0.因r1+r2≤ε,b1≤1- b2= r2,故c1=1-a1-b1-r1=1-b1-r1≥1-(r1+r2)≥1-ε>0,即X1∩X5≠Ø.

下面证明b8=0.若不然,则令a ∈X1∩X5,b∈X2∩X6,c∈X3∩X7,d∈X4∩X8.因此,可以在路v1v2v3v4v5v6v7v8上找到一个重复abcdabcd.综上所述,a8=1-r8.因为a7+a8≤1,所以a7≤1-a8=r8.故b7=1-a7-c7-r7=1-a7-r7≥1-r8-r7≥1-ε.因为b6>ε,所以b7+b6>1,即X6∩X7≠Ø.矛盾.引理8证毕.

引理9 设P8=v1,v2,…,v8.若X3X4X5∈T, 则

1)|X6∩X3|≥(1-2ε)k,且X4X5X6∈T; 或者

2)|X6∩X3|≥(1-2ε)k,|X7∩X4|≥(1-2ε)k,且X5X6X7∈T; 或者

3)|X6∩X4|≥(1-2ε)k,|X7∩X3|≥(1-2ε)k,且X5X6X7∈T.

证明 根据引理8,考虑下面2种情形：

情形1 b6≤ε.由X6∩X5=Ø知c6=0,从而得a6=1-b6-r6≥1-2ε(即|X6∩X3|≥(1-2ε)k ).接下来再分2种情形讨论.

①X6∩X4=Ø.因为X4∩X5=Ø,X5∩X6=Ø,所以X4X5X6∈T.因此,1)成立.

②X6∩X4≠Ø.由引理1知,X7∩X5=Ø,即c7=0,X5X6X7∈T.因为a7+a6≤1,b6=1-a6-c6-r6,所以a7≤b6+r6.又因为r6+r7≤ε,所以b7=1-a7-r7≥1-(b6+r6+r7)≥1-2ε.因此,2)成立.

情形2 a6≤ε.因为X6∩X5=Ø,所以c6=0,因而b6=1-a6-r6≥1-2ε.由X6∩X4≠Ø和引理1知,X7∩X5=Ø,即c7=0,X5X6X7∈T.

因为b7+b6≤1,所以b7≤1-b6=1-(1-a6-r6)= a6+r6.经计算得a7=1-b7-r7≥1-(a6+r6+r7)≥1-2ε.因此,3)成立.引理9证毕.

定义2 设φ:{v1,v2,…,vn}→{A,B,C}是路Pn的一个标号.若存在i, j(i

证明 不妨设X3X4X5∈T, 构造标号φ:{v1,v2,…,vn}→{A,B,C}.令φ(v3)=A,φ(v4)=B,φ(v5)=C.假设φ(vi),φ(vi+1),φ(vi+2)已定义,且c(vi)c(vi+1)c(vi+2)∈T. 根据引理9,下面三者之一成立:

1)|c(vi+3)∩c(vi)|≥(1-2ε)k,且c(vi+1)c(vi+2)c(vi+3)∈T;

2)|c(vi+3)∩c(vi)|≥(1-2ε)k,|c(vi+4)∩c(vi+1)|≥(1-2ε)k,且c(vi+2)c(vi+3)c(vi+4)∈T;

3)|c(vi+3)∩c(vi+1)|≥(1-2ε)k,|c(vi+4)∩c(vi)|≥(1-2ε)k,且c(vi+2)c(vi+3)c(vi+4)∈T.

若1)成立,则令φ(vi+3)=φ(vi);若2)成立,则令φ(vi+3)=φ(vi),φ(vi+4)=φ(vi+1);若3)成立,则令φ(vi+3)=φ(vi+1),φ(vi+4)=φ(vi).依此类推,可根据定义给出所有顶点的标号.由定义2知,对任意的同色伙伴vi,vj,|c(vi)∩c(vj)|≥(1-2ε)k.引理10证毕.

根据引理10,相邻的顶点所给的符号是不同的,所以对于顶点个数为4的路,同一个符号最多出现2 次;对于顶点个数分别为5和6的路,同一个符号最多出现3 次;对于顶点个数为7的路,同一个符号最多出现4 次;对于顶点个数为8的路,同一个符号也最多出现4 次,且这个符号必须标在路的起始顶点上,即形如ABACABCA,否则就有ABACABAC 出现.因此,对于顶点个数为9 的路,同一个符号也最多出现4 次;对于顶点个数依次为10,11,12 的路,同一个符号最多也只能出现5 次；对于顶点个数分别为13和14的路,同一个符号最多也只能出现6 次;对于顶点个数依次为15,16,17的路,同一个符号最多也只能出现7 次.

在圈C14上用3个符号进行标号时,同一个符号最多出现6 次.不妨设这个符号为A,则第1个A与第6个A的交集为[1-6×( 2ε)]k>0.也就是说,对任意的i

在圈C17上用3个符号进行标号时,同一个符号最多出现7 次.不妨设这个符号为A,则第1个A与第7个A 的交集为[1-7×(2ε)]k>0.也就是说,对任意的i

[1]Thue A.Über unendliche Zahlenreihen[J].SelecTed MaThemaTical Papers of Axel Thue,1906(7):139-158.

[2]Alon N,GryTczuk J,Hauszczak M,eT al.NonrepeTiTive colorings of graphs[J].Random STrucTures & AlgoriThms,2002,21(3/4):336-346.

[3]Brešar B,GryTczuk J,Klavžar S,eT al.NonrepeTiTive colorings of Trees[J].DiscreTe MaThemaTics,2007,307(2):163-172.

[4]Currie J D.There are Ternary circular square-free words of lengThnforn≥18[J].ElecTron J Combin,2002,9(1):N10.

[5]Kündgen A,Pelsmajer M J.NonrepeTiTive colorings of graphs of bounded Tree-widTh[J].DiscreTe MaThemaTics,2008,308(19):4473-4478.

[6]GryTczuk J.NonrepeTiTive colourings of graphs——A survey[J].InTernaTional Journal of MaThemaTics and MaThemaTical Sciences,2007,2007:74639.