广义Mycielski 图的边色数

王维凡, 杨灿权

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

本文中所考虑的图都是有限简单图.设V(G),E(G),Δ(G)分别表示图G的顶点集、边集和最大度,将Δ(G)简记为Δ.图的染色理论是图论研究的一个重要内容.图的染色就是对顶点、边等图的元素进行分类,使得它们满足某些特定性质.不同的性质和要求就导出不同的染色方式.图论染色理论中最经典的染色就是正常点染色和正常边染色.本文主要研究图的边染色.

图G的一个正常k-边染色是指一个映射φ:E(G)→{1,2,…,k},使得相邻的边染不同的颜色.图G的边色数χ′(G)定义为最小的正整数k,使得G有一个正常k-边染色.

任意一个最大度为Δ的图G,由于相邻的边需要染不同的颜色,自然可以得到χ′(G)≥Δ.1964年,Vizing[1]证明了下面的一个图论中最重要的结果之一：

定理1[1]对于任意简单图G,Δ≤χ′(G)≤Δ+1.

若χ′(G)=Δ,则称G是第一类的,否则称G是第二类的.对一般图而言,尽管只有2个选择,但要确定是否属于第一类是NP-完全的[2],于是,学者们开始寻找使图G是第一类或第二类图的充分条件.

给定一个最大度为Δ的图G,设GΔ表示由G的所有最大度点导出的子图.基于这个特殊的子图,Fournier[3]给出了下面十分有意义的结果：

定理2[3]对简单图G,若GΔ是一个森林,则G是第一类的.

对于平面图G,Vizing[4]证明了:当Δ≥8时,G是第一类图;而当2≤Δ≤5时,存在第二类的简单平面图G.文献[4]中提出猜想:当6≤Δ≤7时,简单平面图G是第一类的.Sanders等[5]和张利民[6]分别独立证明了当Δ=7时Vizing猜想成立.但当Δ=6时,该猜想至今悬而未决.很多学者给出了部分结果,如考虑不含特殊长度的圈且最大度为6的平面图[7-11].更多关于平面图边染色的结果可以参考文献 [12].

为了研究图的团数与色数之间的关系,Mycielski[13]构造了一类图,称之为Mycielski图,使得它不含三角形但色数可以任意大,从而否定了图的色数会被其团数界定的一个猜想.文献[14-15]提出了广义Mycielski图的概念,并且研究了它的圆环色数、圆环团数、全控制数等若干性质和参数.Tardif[16]也研究了广义Mycielski图的分数染色,给出了一个很漂亮的结果.

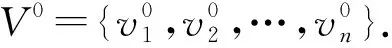
V(μm(G))=V0∪V1∪…∪Vm∪{w};

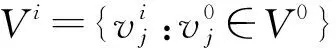
图1 广义Mycielski图μm(G)的示意图

Kwon等[17]证明了：若G是一个不同于K2的连通图,则μ1(G)是第一类图.本文将这个结果推广到广义Mycielski图μm(G),其中m≥2.

1 主要结果

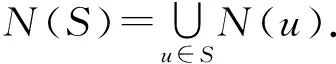
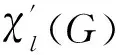
Galvin[18]证明了下面结果:

在定理4的证明之前,需要引入一个重要的引理.

引理1[17]对于整数n≥3,若图G(X∪Y;E)是一个二部图,且满足:

1)|X|=|Y|=n+1;

2)N(X)=Y;

则G含有一个完美匹配.

定理4 设G(≠K2)是一个n-阶简单连通图且m≥2是整数,则χ′(μm(G))=Δ(μm(G)).

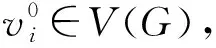
|L(e)|≥|C|-1=Δ+1-1=Δ=Δ(G12).

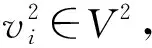
重复以上步骤,并依照奇偶性逐层进行染色,直到μm(G)-w的所有边被正常染色.此外,对第Vk层的顶点标号要求有特殊性质.其中:若m是偶数,则k=m;若m是奇数,则k=m-1.对1≤i≤Δ+1,设Si表示Vk中标颜色ci∈C的顶点集合,且令si=|Si|.于是,类似于文献[17]中引理3.3 的证明,可以要求Vk的标号满足下列附加条件:

(*)对任意2个颜色ci,cj∈C,有|si-sj|≤2.

令s=max{si|i=1,2,…,Δ+1}.由n≤2Δ,n=s1+s2+…+sΔ+1和条件(*),易推出s≤3.

分以下2种情形证明:

1)m是偶数.若对所有i=1,2,…,Δ+1满足si≥1,则选择Si中的某个顶点xi,用颜色b(xi)给边wxi染色.注意到b(xi)∈C,于是与w关联的Δ+1条边被正常染色.剩下的n-(Δ+1)≤2Δ-(Δ+1)=Δ-1条边分别染颜色Δ+2,Δ+3,…,2Δ.进而得到G的一个正常的2Δ-边染色.否则假设存在某些i∈{1,2,…,Δ+1},使得si=0.由条件(*)推出s≤2.对1≤j≤2,定义

Tj={Si: |Si|=j,1≤i≤Δ+1}.

若|T1|+|T2|=Δ+1,则对每一个Si∈T1∪T2,选择Si中的某个顶点xi,用颜色b(xi)给边wxi染色,与w关联的其余n-Δ-1条边分别用Δ+2,Δ+3,…,2Δ染色,从而得到G的一个正常的2Δ-边染色.

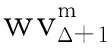
下面将通过改染来完成对与w关联的边染色.主要分2个步骤:

若Δ=3,则n≤2Δ=6.除了|X1|=3外,其余|Xi|均小于3,而|Z∩X1|≤2,故Δ-|Z∩Xi|≥1,其中1≤i≤4.若Δ≥4,因为|Z∩Xi|≤|Xi|≤si≤3,所以对于所有1≤i≤Δ+1,都有Δ- |Z∩Xi|≥1.因而无论哪种情况,对1≤i≤Δ+1,都有Δ-|Z∩Xi|≥1.故对任意颜色ci∈C,都有

d(ci)≥Δ+1-(|Z∩Xi|+1)≥Δ-|Z∩Xi|≥1.

其中括号里的1表示步骤1中换色可能增加的ci-边,而增加的ci-边最多只有一条.这就满足了引理1的条件2),即N(Z)=C.

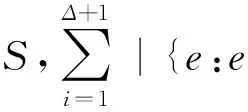
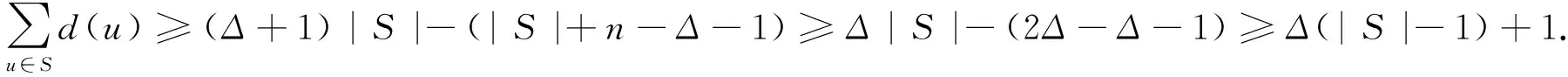
2 结 语

本文证明了:若G是一个不同于K2的连通图,则广义Mycielski图μm(G)(m≥2)是第一类的,即χ′(μm(G))=Δ(μm(G))=max{2Δ(G),|V(G)|}.这个结果推广了文献[17]中m=1时的结论.特别地,当m=0时,若Δ(G)≤n-2,则μ0(G)是第一类的;若Δ(G)=n-1,且n是一个奇数,则μ0(G)也是属于第一类的;但是,若Δ(G)=n-1,且n是一个偶数,问题就变得不那么简单,因为奇阶完全图是属于第二类的.此外,容易看到,当G是K2时,μm(G)是一个奇圈,因此是第二类的.

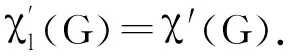
[1]Vizing V G.On an estimate of the chromatic class of ap-graph[J].Metody Diskret Anal,1964,3(7):25-30.

[2]Holyer I.The NP-completeness of edge colorings[J].SIAM J Comput,1981,10(4):718-720.

[3]Fournier J C.Méthode et théorème générale de coloration des arêtes[J].J Math Pures Appl,1977,56(4):437-453.

[4]Vizing V G.Critical graphs with a given chromatic class[J].Diskret Analiz,1965,5(1):9-17.

[5]Sanders D P,Zhao Yue.Planar graphs of maximum degree seven are class I[J].J Combin Theory Ser B,2001,83(2):201-212.

[6]Zhang Limin.Every planar graph with maximum degree 7 is of class one[J].Graphs Combin,2000,16(4):467-495.

[7]Zhou Guofei.A note on graphs of class I[J].Discrete Math,2003,262(1/2/3):339-345.

[8]Bu Yuehua,Wang Weifan.Some sufficient conditions for a planar graph of maximum degree six to be class 1[J].Discrete Math,2006,306(13):1440-1445.

[9]Li Xuechao,Luo Rong,Niu Jianbing.A note on class one graphs with maximum degree six[J].Discrete Math,2006,306(13):1450-1455.

[10]Wang Weifan,Chen Yongzhu.A sufficient condition for a planar graph to be class 1[J].Theoret Comput Sci,2007,385(1/2/3):71-77.

[11]Huang Danjun,Wang Weifan.Planar graphs of Maximum degree six without 7-cycles are class one[J].Electr J Comb,2012,19(3):17-21.

[12]Borodin O V.Coloring of plane graphs:A survey[J].Discrete Math,2013,313(4):517-539.

[13]Mycielski J.Sur le coloriage des graphes[J].Colloq Math,1955,3(161/162):9-12.

[14]Lam P B,Lin Wensong,Gu Guohua,et al.Circular chromatic number and a generalization of construction of Mycielski[J].J Combin Theory Ser B,2003,89(2):195-205.

[15]Lin Wensong,Wu Jianzhuan,Lam P B,et al.Several parameters of generalized Mycielskians[J].Discrete Appl Math,2006,154(8):1173-1182.

[16]Tardif C.Fractional chromatic numbers of cones over graphs[J].J Graph Theory,2001,38(2):87-94.

[17]Kwon Y S,Jee J,Zhang Zhongfu.Edge-chromatic numbers of Mycielski graphs[J].Discrete Math,2012,312(6):1222-1225.

[18]Galvin F.The list chromatic index of a bipartite multigraph[J].J Combin Theory Ser B,1995,63(1):153-158.