变电站电压无功立体模糊控制

张宝杰， 张 超， 杜爱民

(北京电研华源电力技术有限公司，北京 102200)

0 引 言

随着我国电力网络结构的日趋复杂和用户对电能质量要求的不断提升，在系统运行中必须进行电压和无功功率的优化调节.变电站作为联接电网和用户的枢纽，提高变电站电压无功综合控制水平，对保证供电系统电压质量有着现实的重要意义[1].针对现有各种控制策略未综合考虑电压、无功、功率因数3个因素相互影响的缺点，本文利用模糊控制理论善于处理非线性及多因素复杂控制等问题的优点，结合电压、无功变化的特点，提出了变电站电压无功立体模糊控制策略[2-3],其工作原理为：依据电压偏差、无功偏差、功率因数偏差3个输入量的论域，得出它们所对应的模糊词集，再根据模糊词集在模糊控制规则库的位置，得出变压器分接开关调节、电容器组投切2个输出量的模糊词集来控制变压器分接开关的升级和电容器组的投切，以达到调节变电站电压和无功的目的.

1 变电站电压无功立体模糊控制器设计

1.1 模糊输入、输出量

变电站电压无功立体模糊控制器具有电压偏差、无功偏差、功率因数偏差3个输入量和变压器分接开关调节、电容器组投切2个输出量[4].3个出入量关系如图1所示，其中:Eu为电压偏差;Eq为无功偏差;Pf为功率因数偏差.控制目标是使电压无功工作点运行在由Eu,Eq和Pf组成的立体区域内，在该区域内变电站2次侧电压和1次侧功率因数均符合工作要求，具体控制策略详见表1.

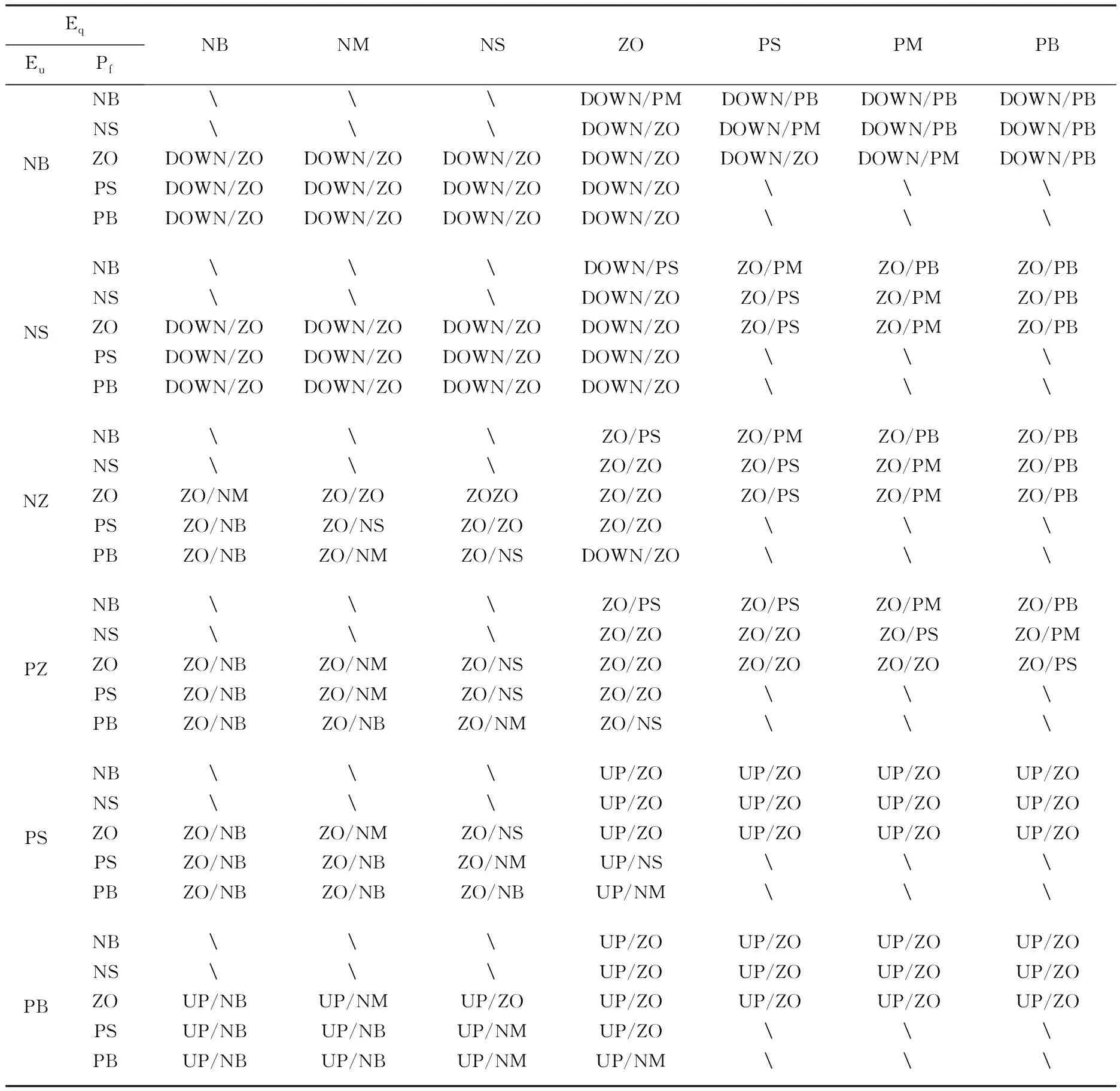
表1 模糊控制规则表

1.2 论域和模糊集的确定

图1 立体模糊输入量模型

模糊控制器的输出变量为变压器分接开关变化量Ut和电容器组的投切量Ct.根据变压器的分接头数，分接开关变化量Ut的基本论域为{-3,-2,-1,0,+1,+2,+3}，论域上的值代表变压器分接开关调节的偏差量，负数定义为降压，正数定义为升压.设电容器组共有3组，则电容器组输出控制变量Ct的基本论域为{-3,-2,-1,0,+1,+2,+3}，论域上的值表示投切电容器的组数，负数定义为切，正数定义为投.

取电压偏差Eu的模糊词集为{NB，NM，NZ，PZ，PM，PB}，其中:NB表示负大;NM表示负中;NZ表示负零;PZ表示正零;PM表示正中;PB表示正大.无功偏差Eq的模糊词集为{NB，NM，NS，ZO，PS，PM，PB},其中:NB表示负大;NM表示负中;NS表示负小;ZO表示零;PS表示正小;PM表示正中;PB表示正大.功率因数偏差Pf的模糊词集为{NB，NS，ZO，PS，PB}，其中:NB表示负大;NS表示负小;ZO表示零;PS表示正小;PB表示正大.由于变压器分接开关严禁发生滑档动作(分接开关连续调节2档以上称为滑档)，因此,变压器每次只能调1档，升降档位的调节量是固定的，对其调节只需要指明分接头是升、降还是不动作，所以分接开关变化量Ut的模糊词集为{DOWN，ZO，UP},其中:UP表示升分接头增大变比(减小电压);ZO表示分接头不动作;DOWN表示降分接头减小变比(增大电压).电容器组的投切量Ct的模糊词集为{NB，NM，NS，ZO，PS，PM，PB}，其中:NB表示负大;NM表示负中;NS表示负小;ZO表示零;PS表示正小;PM表示正中;PB表示正大.考虑模糊集对论域有较好的覆盖程度，按论域中元素总数为模糊词集总数的2～3倍的规律，将模糊输入变量Eu(电压偏差)、Eq(无功偏差)、Pf(功率因数偏差)和模糊输出变量Ct(电容器组投切控制量)均量化为13个等级，即量化论域为{-6,-5,-4,-3,-2,-1,0,1,2,3, 4,5,6}，而输出变量Ut(分接头控制量)的量化论域为{-4,-3,-2,-1,0,1,2,3,4}.所以,输入变量Eu,Eq,Pf的量化因子分别为：K1=6/0.15=40;K2=6/3=2;K3=6/0.25=24.输出变量Ut,Ct的比例因子分别为：K4=3/4=0.75;K5=3/6=0.5.变电站电压无功综合控制模糊系统编辑窗口如图2所示.

图2 模糊系统编辑窗口

1.3 隶属度函数和模糊控制规则的确定

输入、输出控制量的隶属度函数采用梯形隶属度函数.

根据所选择的输入与输出变量的模糊词集和隶属度函数特点，结合电压无功综合调节需遵守的一些规章规程和专家经验.可得到如表1所示的控制规则.表1中,分子对应于变压器分接头的模糊输出量为Ut，分母对应于电容器投切的模糊输出量为Ct.

由于变电站主要考核指标是进线侧(一次侧)功率因数和二次侧母线电压，所以,上述控制规则库综合考虑了电压、无功、功率因数三要素的相互影响，保证了电压、功率因数合格，具体控制策略如下：无功偏差量在{NB，NM，NS}，功率因数在{NB，NS}，该区域按无功控制需切无功，而按功率因数控制则需投无功，这是相互矛盾的，所以,无论电压偏差为何值，该区域在实际中是不存在的，在控制表中表现为“”部分.同理，无功偏差在{PB，PM，PS}，功率因数在{PB，PS}，所对应区域同样是实际不存在区.

电压偏差量在{NZ，PZ}，此时电压合格，为电压不控制区.当无功偏差在{NB，NM，NS}，功率因数在{PB，PS}，表示无功过剩、功率因数高，需要切电容；当无功偏差在{PB，PM，PS}，功率因数在{NB，NS}时，表示无功不足、功率因数低，需要投电容.具体电容器的投切量当电压偏差在正零(PZ)或负零(NZ)时，如表1所示有所不同.

电压偏差量在NS，电压稍微偏低.当无功偏差在{NB，NM，NS}，功率因数在{PB，PS}时，表示无功过剩、功率因数高，变压器降档升压；当无功偏差在{PB，PM，PS}，功率因数在{NB，NS}时，表示无功不足、功率因数低，在该区域内变压器分接头不动作，投电容.

电压偏差量在NB，表示电压非常低.当无功偏差在{NB，NM，NS}，功率因数在{PB，PS}时，表示无功过剩、功率因数高，变压器降档升压，如变压器已在最低档,则只能牺牲无功,保证电压合格；当无功偏差在{PB，PM，PS}，功率因数在{NB，NS}时，表示无功不足、功率因数低，在该区域内投入较多电容:如电容全部投完，电压仍然偏低，则变压器降档升压.

电压偏差量在PS，电压稍微偏高.当无功偏差在{NB，NM，NS}，功率因数在{PB，PS}时，表示无功过剩、功率因数高，此处变压器分接开关不动作，切电容；当无功偏差在{PB，PM，PS}，功率因数在{NB，NS}时，表示无功不足、功率因数低，变压器升档降压.

电压偏差量在PB，表示电压非常高.当无功偏差在{NB，NM，NS}，功率因数在{PB，PS}时，表示无功过剩、功率因数高，此处切电容;电容切完后如果电压仍然偏高，则升档降压.当无功偏差在{PB，PM，PS}时，功率因数在{NB，NS}时，表示无功不足、功率因数低，在该区域内变压器升档降压[5].

1.4 模糊控制曲面图分析

由图3和图4可得到如下结论:

图3 分接头控制策略三维曲面图

1)Ut是改善电压的直接参数，Ct是平衡无功功率、改善功率因数的主要参数.

2)当电压偏差不在合格范围内时，无论功率因数合格与否，都要通过调节Ut和Ct来确保电压运行在合格范围内.

3)当电压偏差较小(在合格范围内)时，分接头不动作；当电压偏差为正大时升档降压；当电压偏差为负大时降档升压.

4)电压偏差为负小时，无功偏差为负、功率因数为正，降档升压，在升高电压的同时，可提高无功偏差降低功率因数；无功偏差为正、功率因数为负，分接头不动作，投入适量电容器组，在降低无功偏差提高功率因数的同时，可使电压升高；同理可分析电压偏差为正小时分接头和电容器组的动作状态.

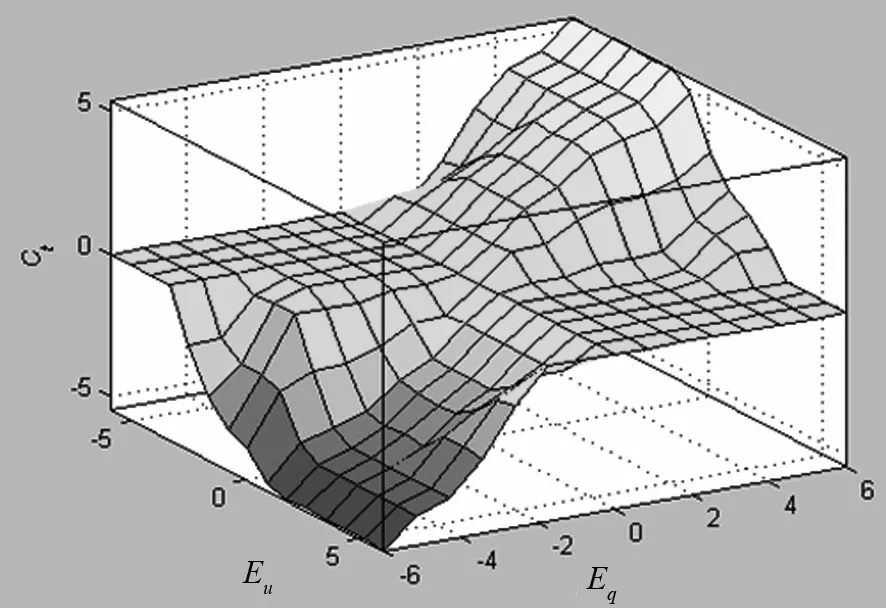
图4 电容器投切控制策略三维曲面图

5)电压偏差为负大时，无功偏差为负、功率因数为正，降档升压，在升高电压的同时，可提高无功偏差降低功率因数；无功偏差为正、功率因数为负，投入适量电容器组，在降低无功偏差提高功率因数的同时，可使电压升高，如电压仍然较低则降档升压；同理可分析电压偏差为正大时分接头和电容器组的动作状态.

6)可以直观地看出在保证电压、功率因数合格的同时有效地减少了分接开关的动作次数和电容器组的投切次数.

1.5 变电站电压无功立体模糊控制仿真分析

利用MATLAB搭建变电站的仿真模型如图5所示.导线采用LGJ-185，水平排列，线路长100km,有载调压变压器型号SFZL1-31500/110，额定电压(110±32.5%/6.3)kV，线路r0=0.17Ω/km，x0=0.394Ω/km，变压器：短路损耗Pd=196.9kW，空载损耗P0=29.6kW，短路电压百分数Ud%=10.5，空载电流百分数I0%=0.7，连接方式为YG，d11.电容器2 800kVAR，共3组.

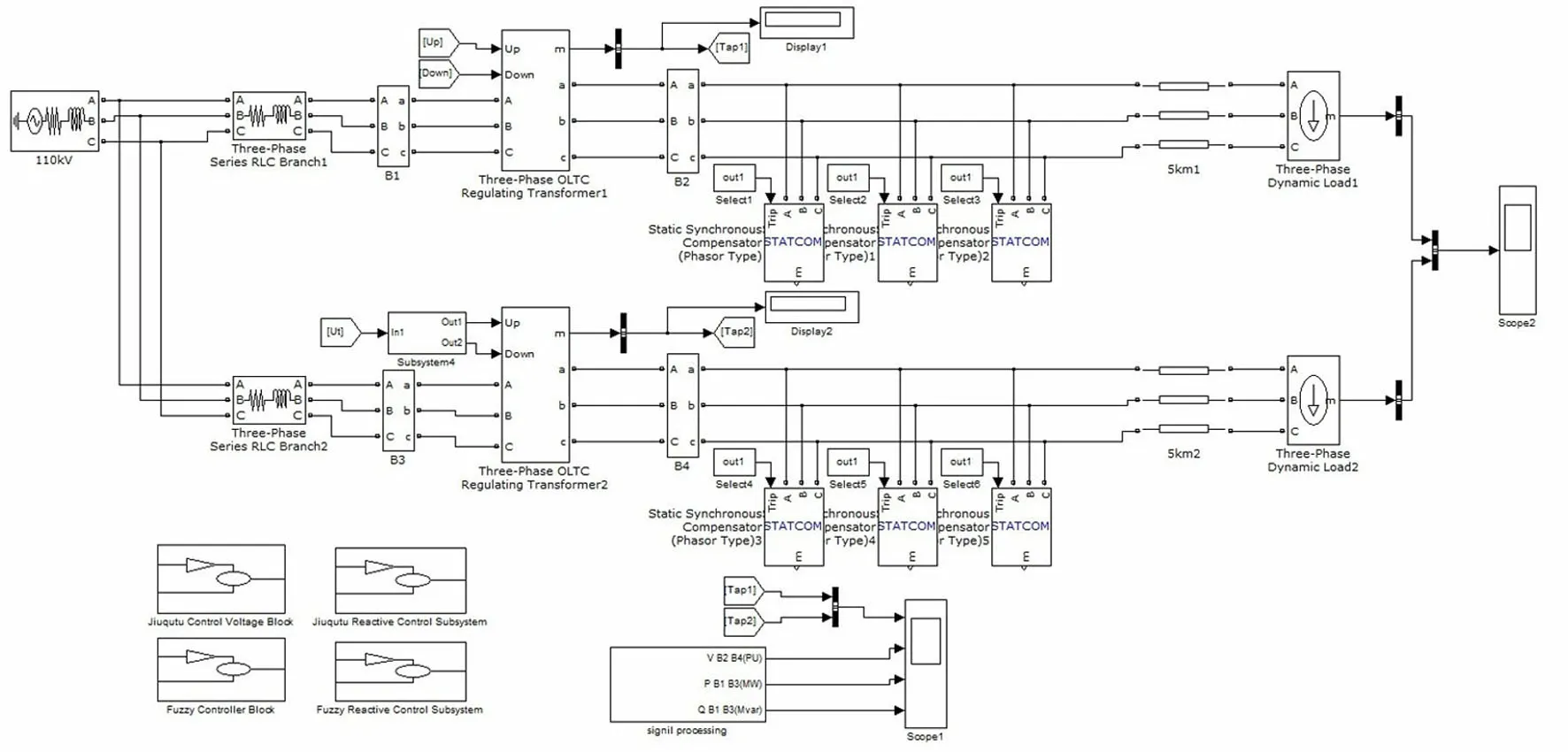
图5 变电站电压无功立体模糊控制仿真模型

此仿真是针对线路1和线路2分别进行的.其中线路1通过九区图控制策略对变压器分接开关和无功补偿装置进行调节；而线路2通过立体模糊控制分别对变压器分接开关和无功补偿装置进行调节.运行仿真模型可得示波器1和示波器2,图形如图6、图7所示.

图6 示波器1仿真结果 图7 示波器2(用户端电压)仿真结果

图6、图7中,粉线为线路1的仿真结果;黄线为线路2的仿真结果，具体分析如下：

1)Tapl，Tap2(变压器分接开关档位)：由于线路2模型中采用立体模糊控制对变压器分接开关进行调节，从仿真结果中可以明显看出其分接开关调节次数比采用九区图控制策略的线路1模型的调节次数少.

2)VB2,VB4(pu)：VB2,VB4分别为线路1、线路2中变压器二次侧电压.可以看出，通过立体模糊控制的系统其仿真输出的黄线比通过九区图控制的粉线波动小,波动次数也明显少，说明使用立体模糊控制比使用九区图控制的变压器二次侧电压更加稳定.

3)PB1,PB3(MW)：PB1,PB3分别为线路1、线路2中变压器一次侧有功功率.由于2个模型所带负载相同，所以消耗的有功功率应该相同，仿真结果显示，2个模型的变压器一次侧有功功率基本一致，可见实际仿真结果与理论分析相一致.

4)QB1,QB3(MVar)：QB1,QB3分别为线路1、线路2中变压器一次侧无功功率.由仿真结果可见，线路1中变压器一次侧的输入无功比线路2中变压器一次侧的输入无功要多，系统中传输较多的无功会造成系统网损增加、电压下降，由此可见,使用立体模糊控制比使用九区图控制进行无功补偿的效果更好.

5)示波器2：如图7所示，线路2经过立体模糊控制的用户端电压比线路1经过九区图控制的用户端电压波动更小，更加平稳.

2 结束语

本文提出的变电站电压无功立体模糊控制策略，充分考虑了电压、无功和功率因数的相互关系，相比九区图控制策略来说，更能提高供电电压的质量,有效地减少了输电线路的无功功率传输和有载调压变压器分接开关的动作次数，进而延长了变压器的使用寿命，提升了整个电力系统的电压稳定状况.利用MATLAB搭建变电站电压无功立体模糊控制和九区图控制的对比仿真模型，通过仿真分析，验证立体模糊控制的优越性及可行性.

[1]张小英，池瑞军，胡奉东，等.变电站电压无功综合控制策略的研究[J].湖北电力，2004，28(3)：13-14；17.

[2]Lu Fengchang,Hsu Y Y.Fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation[J].IEEE Trans on Power Systems,1997,12(2)：681-688.

[3]陈晓光,唐刚,江均.基于变电站电压无功综合调节的模糊控制研究[J].四川电力技术,2008,31(11)：7-9.

[4]Kovacic Z,Bogdan S.Fuzzy controller design:theory and applications[M].Florida:CRC Press,2005.

[5]张明军，厉吉文，董洁.模糊边界的电压无功调节判据[J].电力自动化设备，2004，24(11)：58-59.