一道课后习题的多种解法

●付中华

(乳源高级中学 广东韶关 512700)

课后习题是对课本知识的巩固和加深，很多高考题都能找到课本习题的影子.对于课后习题，在教学时，不能就题论题，要倡导学生一题多解、一题多思、一题多变，培养学生的发散思维能力和创新能力.

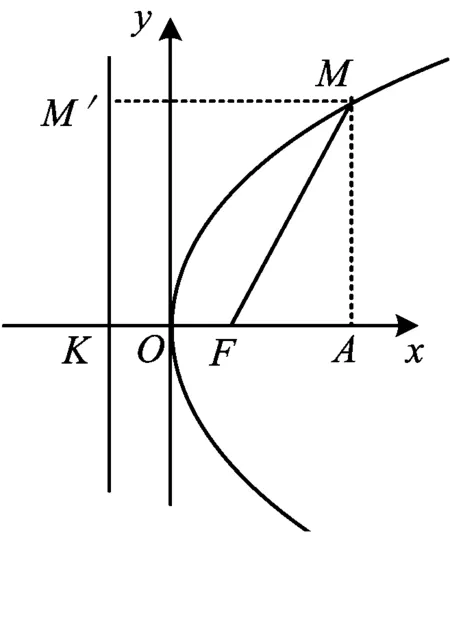
图1

1 问题呈现

人教版选修2-1(A版)第73页习题：

如图1，M是抛物线y2=4x上一点，F是抛物线的焦点，以Fx为始边、FM为终边的角∠xFM=60°，求|FM|.

2 问题解析

解法1 由题设知线段FM所在直线的斜率为

从而直线FM的方程为

与抛物线y2=4x联立，得

解得

评注 从“数”的角度出发，求出交点的坐标后，利用两点间距离公式即得.

变式1 设F为抛物线C:y2=4x的焦点，过点P(-1,0)的直线l交抛物线C于点A,B，点O为线段AB的中点，若|FQ|=2,则直线的斜率等于______.

(2013年浙江省数学高考试题)

分析 由题知F(1,0)，设l的方程为

y=k(x+1)(k≠0)，

联立y2=4x得

k2x2+(2k2-4)x+k2=0.

设A(x1,y1),B(x2,y2),Q(x0,y0)，则

解得

k=±1.

解法2 如图1，由抛物线y2=4x知F(1,0)，|KF|=p=2.过点M作MA⊥x轴，垂足为A，作MM′⊥l，垂足为M′，则

设计意图 数学思想方法是数学知识的精髓和灵魂，是架起知识转化为能力的桥梁和纽带，通过引导学生回顾线面平行和线面垂直的判定定理，让学生体会定理蕴涵的数学思想方法，掌握研究立体几何的基本方法，完善良好的认知结构，从而实现学生思维能力和创新能力的提升.

在高中数学教学中，教师既要尊重教材，正确驾驭和把握教材的核心内容和科学体系，又要立足于学生的实际水平，把培养和发展学生的思维作为主要目标，从而创造性地运用教材，不能为了实现知识和技能的目标而人为地降低教学任务.

(注：本文是浙江省教科规划项目“师范生微格教学高效性策略的研究与实践(编号：SCG003)”、山西省高等学校教育教学研究项目“《数学的文化价值》课程设计与实践研究(编号：J2012083)”的阶段性成果.)

[1] 单墫.数学是思维的科学[J].数学通报,2001(6):1-2.

[2] 胡芳举.巧证线面垂直的判定定理[J].数学通讯,2007(9):20-21.

[3] 罗建中.直线与平面垂直的新证法[J].数学教学研究，2004(6)：15-16.

|MF|= |MM′|=|KA|=|KF|+|FA|=

|KF|+|MF|cos60°=

从而

MF=2|KF|=4.

评注 从“形”的角度出发，利用矩形及直角三角形中角与边的关系，再结合抛物线的定义求解.

图2

推广到一般情形：如图2，M是抛物线y2=2px(p>0)上一点，F是抛物线的焦点，以Fx为始边、FM为终边的角∠xFM=θ，则

( )

(2013年全国数学高考新课标卷试题)

分析 设∠xFP=θ，则

得

即

θ=60°，

故选C.

变式3 设抛物线C:y2=4x的焦点为F,直线l过点F且与C交于点A,B.若|AF|=3|BF|,则l的方程为

( )

A．y=x-1或y=-x+1

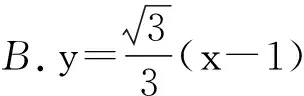
(2013年全国数学高考新课标卷试题)

分析 易知p=2，F(1,0).设∠xFA=θ，则

从而

得

即

θ=60°.

解法3 如图3，过点M作MM′⊥l，垂足为M′，联结M′F，易知∠FMM′=60°.由抛物线的定义知|MF|=|MM′|，从而△FMM′为正三角形，于是

∠MFM′=60°,∠KFM′=60°.

在Rt△KFM′中，因为

|KF|=2,|M′F|=4,

所以

|MF|=|M′F|=4.

评注 利用抛物线的定义和已知条件巧妙地构造Rt△KFM′和正△MFM′快速求解.

图3 图4

解法4 如图4，延长线段MF交l于点G，过点M作MM′⊥l，垂足为M′.在Rt△KFG中,

∠KFG=∠xFM=60°，∠FGK=30°,

|KF|=p=2,|GF|=4;

在Rt△MGM′中,

∠FGK=30°,2|MM′|=|MG|,

即

2|MF|=|MF|+4，

故|MF|=4.

评注 利用抛物线的定义和已知条件巧妙地构造Rt△KGM′和△Rt△MGM′，从而求解.

(2013年福建省数学高考试题)

∠MF1F2=60°,∠MF2F1=30°，∠F2MF1=90°，