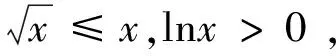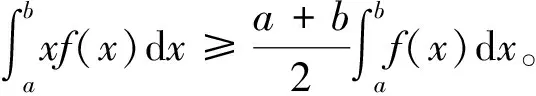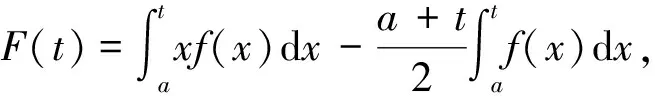数学分析中的不等式证明问题*1
王 建 莉
(包头师范学院 数学科学学院,内蒙古 包头 014030)
1 引言
不等式是数学分析的基本内容之一,它是研究许多数学分支的重要工具。在数学领域中占有重要的地位,也是各个时期的数学教材的重要组成部分,在各种考试和竞赛中都有举足轻重的地位。本文介绍的三种证明不等式的方法、拉格朗日中值定理法、柯西中值定理法和定积分理论法。希望通过对这三种方法的学习,我们可以很好的认识数学的一些特点,从而开拓一下我们的数学视野,深化一下我们对不等式证明方法的认识,以便于可以站在更高的角度来研究数学不等式。
2 用拉格朗日中值定理证明不等式法
2.1 定理内容
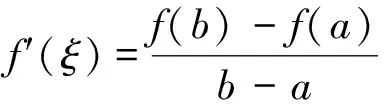
2.2 证明思路
(1)确定函数f(x)施用拉格朗日中值定理的区间[a,b];
(2)对f(x)在[a,b]上施用拉格朗日中值定理;
(3)利用ξ与a,b的关系,由拉格朗日中值公式得到所要证明的不等式。
2.3 适用范围
当所证的不等式中含有函数值的差或区间端点值的差,可用拉格朗日中值定理来证明。
2.4 例题分析
例1:设f(x)在[a,b]上连续,在(a,b)上可微,f′(x)在(a,b)内单调递增。
证明:对任意x1,x2∈[a,b]及λ∈[0,1],有
f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)
(1)
证明:显然当λ=0或λ=1时,(1)式显然成立,因此只讨论λ∈(0,1)即可。
∀x1,x2∈[a,b],不失一般性,设x1 由拉格朗日中值定理,知∃ξ∈(x,x),∃η∈(x,x2),使得 λ[f(x)-f(x1)]+(1-λ)[f(x)-f(x2)]=λf′(ξ)(x-x1)+(1-λ)f′(η)(x-x2) (2) 根据 x-x1=[λx1+(1-λ)x2]-x2=(1-λ)(x2-x1) (3) x-x2=[λx1+(1-λ)x2]-x2=λ(x1-x2) (4) 将(3) (4)代入(2)有 λ[f(x)-f(x1)]+(1-λ)[f(x)-f(x2)]=λf′(ξ)((1-λ)(x2-x1)+(1-λ)f′(η)λ(x1-x2) =λ(1-λ)(x2-x1)[f′(ξ)-f′(η)] (5) 由已知f′(x)在(a,b)内单调递增 ,根据x1<ξ f′(ξ)-f′(η)≤0 。 由(5)得 λ[f(x)-f(x1)]+(1-λ)[f(x)-f(x2)]≤0。 即: f(x)≤λf(x1) + (1-λ)f(x2)。 f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)。 (1)构造两个辅助函数f(x)和g(x),并确定它们施用柯西中值定理的区间[a,b]; (2)对f(x)与g(x)在[a,b]上施用柯西中值定理; (3)利用ξ与a,b的关系,对柯西公式进行加强不等式。 当不等式含有两个函数的函数值及其一阶导数,或两个函数的函数增量及其一阶导数时,可用柯西中值定理证明。 有 因此 即 ay-ax>(cosx-cosy)axlna。 当不等式含有定积分(或被积函数f(x)≤g(x)时),可用定积分的性质证明或构造以积分上限的函数作为辅助函数来证明。 证明:设辅助函数 由f(x)在[a,b]上的连续性,知F(t)在[a,b]可导,且∀t∈[a,b] ,有 根据已知f(x)在[a,b]单调递增,则当x∈[a,t]⊂[a,b] 时,有f(t)-f(x)≥0,于是F′(t)≥0。从而知F(t)在[a,b]单调递增。所以F(b)≥F(a)=0。 (b≥a)。于是有 拉格朗日中值定理,柯西中值定理,定积分理论在数学分析中都有很多的应用,不等式的证明方法也有很多,本文只对拉格朗日中值定理法,柯西中值定理法,定积分理论法作了一部分的归纳总结,目的是在于启发思路;通过对不等式证明的分析以提高分析问题,解决问题的能力,提高逻辑思维能力。 〔参考文献〕 [1]刘玉琏,傅沛仁.数学分析讲义[M].吉林:东北师范大学出版社,2003:240-267. [2]钱吉林,张祖发.数学分析题解精粹[M].北京:崇文书局,195-196. [3]斐礼文.数学分析中的典型问题与方法(第二版)[M].北京:高等教育出版社:261-288,345-349. [4]华东师范大学数学系编.数学分析[M].北京:高等教育出版社. [5]吉米多维奇.数学分析习题集题解[M].山东:山东科学技术出版社.3 用柯西中值定理证明不等式法
3.1 定理内容

3.2 证明思路
3.3 适用范围
3.4 例题分析
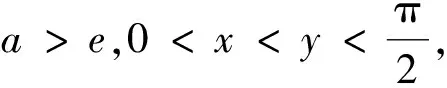
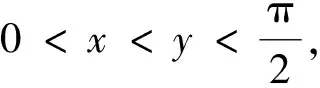
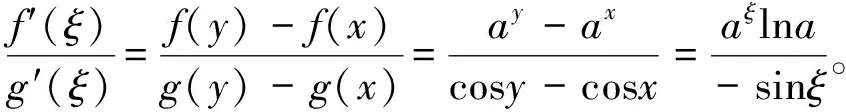
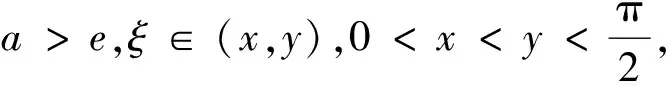
4 定积分不等式的证明
4.1 证明思路
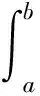
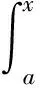
4.2 适用范围
4.3 例题分析