级数收敛意义下的一个循环小数的加法问题*1

胡 利 军

(包头师范学院 教育科学学院 内蒙古 包头 014030)

由于循环小数和分数可以互化，因此在加法运算中会产生下面的问题：

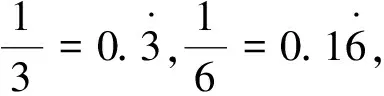
对吗？

而且还可以有

等.

根据小数的数位表，把循环小数表示成不同计数单位上数的和的形式，有下列两式：

(1)

(2)

根据级数的意义，上述(1)、(2)两式的右端显然是两个收敛的正项级数：

(4)

收敛级数的定义为[1]：对于级数

u1+u2+u3+…+un+…(*),

其部分和数列为

sn=u1+u2+u3+…+un,

若级数(*)的部分和数列{sn}收敛.设

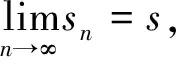
则称级数(*)收敛，s是级数(*)的和，表为

根据级数收敛的定义，级数(3)和(4)都是收敛的.这是因为

对于级数(3)、(4)其n项部分和数列{sn1}和{sn2}分别是

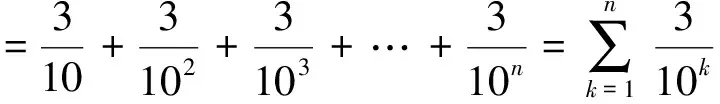
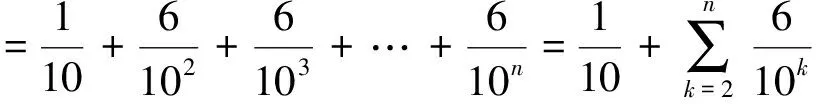
注意到收敛级数有这样一个性质：

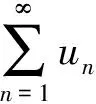
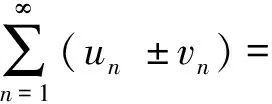
(u3±v3)+…+(un±vn)+…

也收敛，其和是A±B.

根据这个性质，级数(4)、(5)的和也是收敛的，设其和为s,则

这样，在收敛级数的意义下，

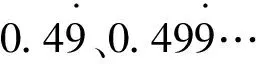
而且级数(4)、(5)的n项部分和数列{sn1}和{sn2}均收敛，设分别s1、s2即

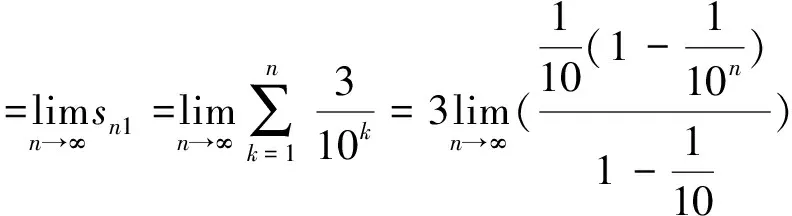
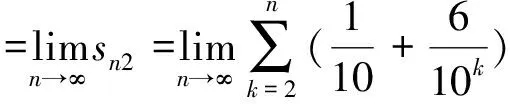
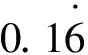
一般地，每一个循环小数都可以利用一个特殊的幂级数

∑anxn=a0+a1x1+a2x2+…+anxn+…，

其中，令

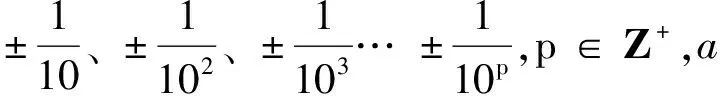
这个幂级数的和为:

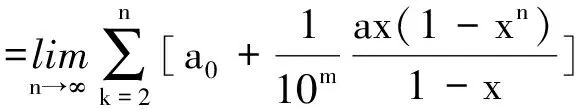
由此式，就可以把任何一个循环小数拆成循环部分加上不循环部分[3].在收敛级数的意义下，类似于上述运算的一些实际问题也是容易给出合理的解释。

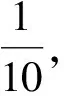
解：设这两条曲线共长L.其中第一条和第二条曲线的长分别是L1、L2，L=L1+L2.

由于

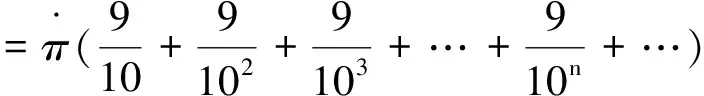
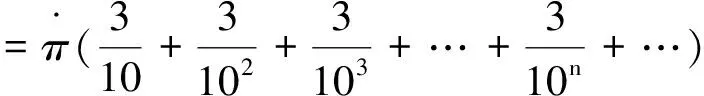
所以

显然，此答案的获得，正是利用了收敛级数的性质.

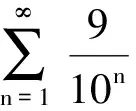
当然，利用循环小数，两条曲线的长可以表示为：

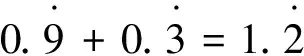
关于这个问题，可以简单地解释为：碰到循环节首位数相加需要进位时，循环节的末位也要进位.这个进位数可以看做是后一个循环节向前一循环节进位得到的[2].如果追问：为什么要这样进位？回答这个问题，如果能用级数收敛来解释，就很有说服力了。这个说理在上面的求曲线长的问题中，已经用级数收敛的意义给出了答案.

〔参考文献〕

[1]义务教育课程标准实验教科书(五年级下册)[M].北京：人民教育出版社，2005.

[2]叶小峰. 循环小数怎样相加减[J]. 小学数学(教学版), 2007,11(11):24-25.

[3]刘玉琏，等. 数学分析讲义(第五版)[M].北京： 高等教育出版社，2008，5, 4.

[4]陈占靖. 利用幂级数计算某类循环小数[J]. 教学交流,2011,9.

[5]郜舒竹. 为教师的微积分[M].北京：高等教育出版社，2012,7.