基于差分进化算子的遗传算法在多波束平面阵天线综合中的应用∗

章仁婷， 梁 广， 余金培

(1中国科学院 上海微系统与信息技术研究所 上海 200050 2上海微小卫星工程中心 上海 201203)

基于差分进化算子的遗传算法在多波束平面阵天线综合中的应用∗

章仁婷， 梁 广， 余金培

(1中国科学院 上海微系统与信息技术研究所 上海 200050 2上海微小卫星工程中心 上海 201203)

针对大角度扫描的低轨卫星多波束平面阵天线，提出一种基于差分进化算子的遗传算法，分别对阵列天线的幅度和相位激励权重进行综合优化。算法采用结合差分进化操作的遗传算子更新种群因子，不仅改善了算法的收敛速度，而且优化了综合结果。仿真结果表明，算法能有效应用于平面阵天线的综合，并取得符合各项设计指标的优化解。实测结果验证了平面阵天线辐射场模型的正确性和算法的可行性。

多波束平面阵天线； 天线综合； 遗传算法； 差分操作

引言

随着全球信息化时代的到来，卫星移动通信日渐成为构建全球通信网的关键组成部分，其中，低轨卫星系统以其较短的传播时延、较低的路径损耗和用户终端小型化等特点受到广泛关注[1]。低轨卫星通信系统要求卫星天线波束具有较高增益和较宽张角，为此，采用多个波束叠加覆盖，并对各个波束进行特殊赋形，这不仅大大增加了卫星天线的等效全向辐射功率EIRP和品质因数G/T值，而且可以有效地进行极化隔离和空间隔离，实现频谱复用，从而成倍增加通信容量[2]。

本文主要针对正六边形19阵元平面阵天线[3，4]进行多波束阵列天线综合。传统的阵列天线综合方法(如切比雪夫(Chebyshev)、泰勒(Taylor)、伍德沃德(Woodward)等方法)已经无法有效解决多参数非线性平面阵天线综合优化问题。近年来，越来越多的智能优化算法(如遗传算法、粒子群算法、模拟退火算法、差分进化算法等)被用来解决大规模阵列天线的方向图综合问题。本文基于实际工程应用需要，对正六边形19阵元平面阵天线的理想辐射方向图进行建模，根据相应工程指标定义目标函数，提出一种改进的遗传算法对平面阵天线进行综合优化，通过引入差分进化算子，迭代更新阵元幅度和相位激励权重，最终得到七个波束赋形优化结果。仿真与实测结果表明，与传统遗传算法相比，该算法收敛速度较快，优化效果显著，能够得到有效工程解。

1 多波束平面阵天线

1.1 正六边形平面阵列天线模型

实际应用天线模型如图1所示，19阵元正六边形平面阵采用三角形栅格排布，以节省辐射元器件[5，6]。阵列天线综合的目标是通过调整天线各单元的幅度和相位激励权重，使得实际天线方向图与目标天线方向图一致。为此首先对阵列天线的理想辐射方向图进行建模，以天线辐射中心为坐标原点建立坐标系，则阵因子为

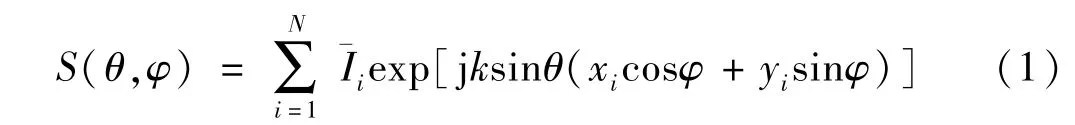
图1 六边形平面阵列天线模型

六边形平面阵天线的19个阵元按照图1顺序排列，由于工艺和互耦影响造成阵元之间存在差异，因此单元因子无法使用统一的天线单元方向图函数表示，则式(2)可表示为

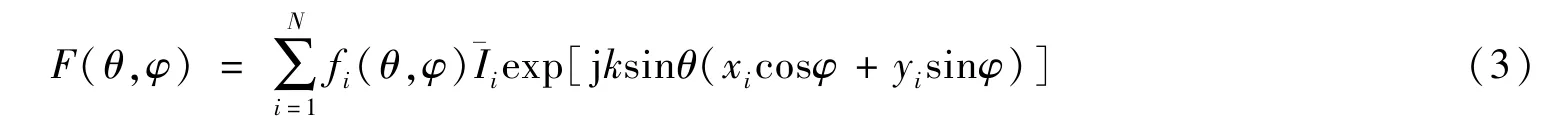
其中fi(θ，φ)为阵元i的本征激励方向图函数。将六边形阵列的某个阵元接激励信号源，其余所有单元接阻抗值与信号源相同的无源负载，对应测得该阵元的本征激励方向图，图2所示为四个不同位置阵元的本征激励方向图。

图2 不同阵元本征激励方向图比较

整个六边形平面阵天线方向性系数D可由式(4)求得。

1.2 定义目标函数

为了补偿大覆盖张角带来的星地间传输路径损耗差异，对波束空间进行如图3所示的规划，将覆盖区域分为两层波束(1，6)覆盖，外层6个波束按照中心60°对称依次排列。设定天线综合目标：中心波束主瓣区域在俯仰角范围0°～30°，方位角全360°，要求主瓣尽量展宽，且增益在10dB以上，旁瓣抑制度不大于－15dB；其它边缘波束(以图3所示波束2为例)，俯仰角范围30°～55°，方位角范围－30°～30°，主瓣区域内增益尽量抬高在12dB以上，旁瓣抑制度不大于－15dB。考虑要使实际方向图逼近目标方向图，构造适应度函数如下

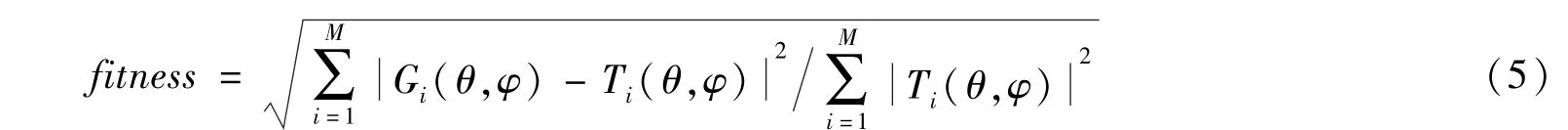
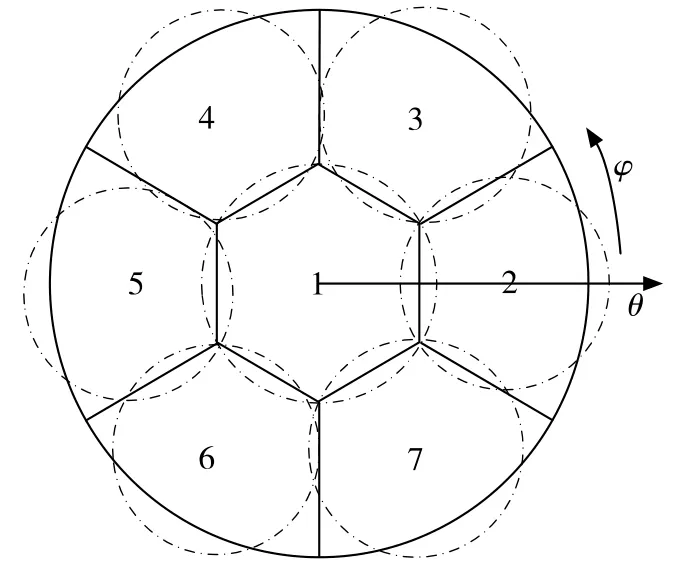
图3 七波束空间规划

其中，M表示方向图的采样点数，Gi(θ，φ)和Ti(θ，φ)分别是增益方向图在采样点上的增益实际值和目标值。

2 基于差分进化算子的遗传算法

遗传算法GA(Genetic Algorithm)是1967年由美国Holland教授提出的一种模拟生物进化的全局搜索算法[7，8]。GA是一种群体型操作，以群体中的所有个体为对象，通过随机选择、交叉和变异操作，迭代更新种群因子，使群体向适应度好的方向优化，直至满足终止条件。

本文基于遗传算法，结合差分进化算子，针对多波束天线综合提出一种改进的混合遗传优化算法，与传统遗传算法相比，改进算法不仅提高了算法优化效率，而且在一定程度上拓展了搜索空间，改善了平面阵天线方向图综合出的最优解。

2.1 传统遗传算法

遗传算法不同于传统搜索算法，它的搜索过程起始于“种群”，每个种群个体都是问题的一个解。在每一代的进化中，用适应度函数值来评价种群个体的好坏，后生成的种群个体通过上一代种群个体间的遗传操作(如选择、交叉、变异)形成，并不断朝着适应度好的方向进化，通过多次迭代算法将收敛于最优个体[9，10]。

传统遗传算法的求解过程如图4所示，它仅当满足终止条件时跳出循环。

图4 传统遗传算法求解过程

2.2 差分进化算子迭代更新

差分进化算子是1995年Stone R和Price K提出的差分进化算法的特有操作算子，它与传统单一的遗传操作不同，在每一个新个体的生成过程中用到了两个以上的父代个体的线性组合，这样就有更多的遗传信息进入到下一代[11]。

(1)变异

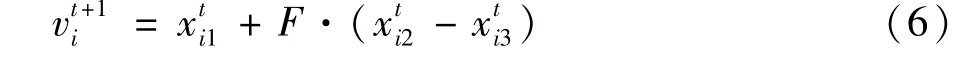
其中，F是缩放因子，用于控制差分项的幅度，取值范围为[0，2]。变异个体通过父代个体的基因值差分计算产生，即在父代种群中随机选取三个个体之间的矢量差进行缩放，再与另一个个体相加，生成变异个体

(2)交叉

为了确保种群个体多样性，引入交叉操作，交叉个体每一维的基因值在父代种群个体和变异个体间随机选取，要保证交叉个体中至少有一维基因值是由变异个体提供的。其操作如下

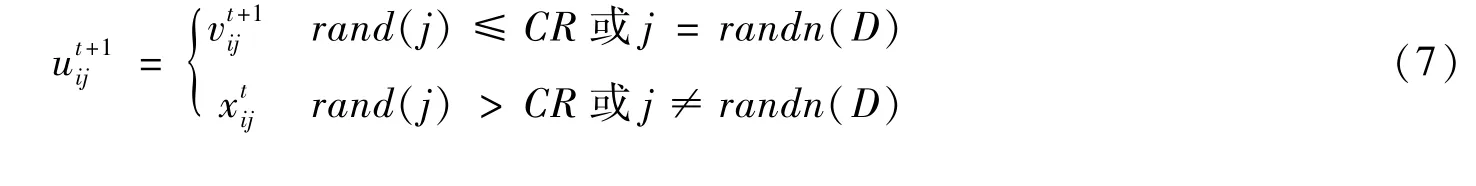
其中，rand(j)是[0，1]之间的随机小数；CR是交叉因子，表示的是变异交叉的概率，取值范围为[0，1]；randn(D)是[1，2，…，D]的随机整数。

其中，a、b分别为个体基因值上、下界，rand是[0，1]之间的随机小数，表示变异时选取个体的第j维基因值。

(3)选择

为了确定交叉后的个体能否成为下一代个体，采用“贪婪”准则，将当前种群个体与经历变异交叉后的个体进行竞争，只有适应度好的才被保留。选择操作如式(10)，其中表示相应个体的适应度函数值。

色谱柱：xbridge TMC18柱(4.6 mm×250 mm，5 μm)、检测波长278 nm、柱温40℃、流速0.8 ml/min、进样量20 μl。流动相比例：V（甲醇）∶V（水）（0.2%磷酸氢二铵缓冲液，pH值5.0）=40∶60。

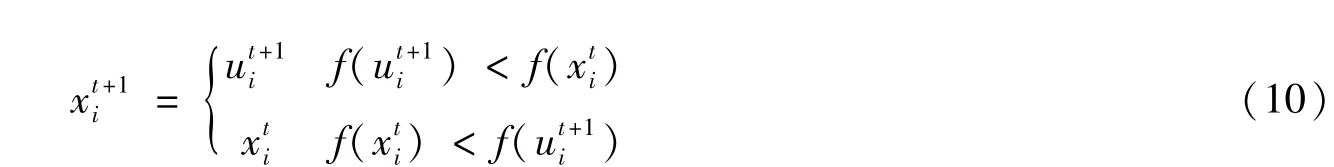
2.3 改进算法具体实现步骤

本文算法在传统遗传算法的基础上，利用差分进化操作，使用一系列的差分组合方式产生多个个体，然后选择最优个体进入下一代，并使用最优保留策略保留种群里未参与进化操作的适应度最好的个体。采用这种进化策略可以很好地拓展搜寻空间，同时保证算法的收敛性。改进算法具体实现步骤如下：

步骤1：使用实数编码方式产生初始种群，与二进制编码方式相比，可有效提高求解的精度，还能避免计算过程中的编码和解码操作，降低算法复杂性。

步骤2：设计适应度函数，并计算每个个体的适应度函数值。直接选择式(5)定义的目标函数作为适应度评价标准。

步骤3：采用轮盘赌方法，即以个体适应度函数值为依据选择再生个体，个体被选中概率与适应度函数值大小成正比，设种群规模为n，种群个体i适应度函数值为fi，则该个体被选择概率pi如式(11)所示。

步骤4：按照2.2节描述，使用差分进化操作产生下一代个体，保证下一代种群的多样性和进化的有效性。

步骤5：使用最优保留策略，即将当前群体中适应度最高的个体直接复制到下一代，保证所得到的最优个体不会被交叉、变异等进化操作所破坏，提高算法的运行效率和收敛性。

步骤6：重复步骤2～5，直至优化结果满足条件或达到规定迭代次数，输出最优结果。

3 仿真与实测结果分析

采用两种算法分别对中心波束1和边缘波束2赋形，迭代次数均为500代，其他设置不变，综合结果分别如图6和图7所示。由图6、图7可以看出，与传统遗传算法相比，本文算法的优化效果更为明显，波瓣宽度展宽3°～4°，旁瓣抑制度降低了5dB以上，符合工程设计要求。

图5 算法收敛性能比较

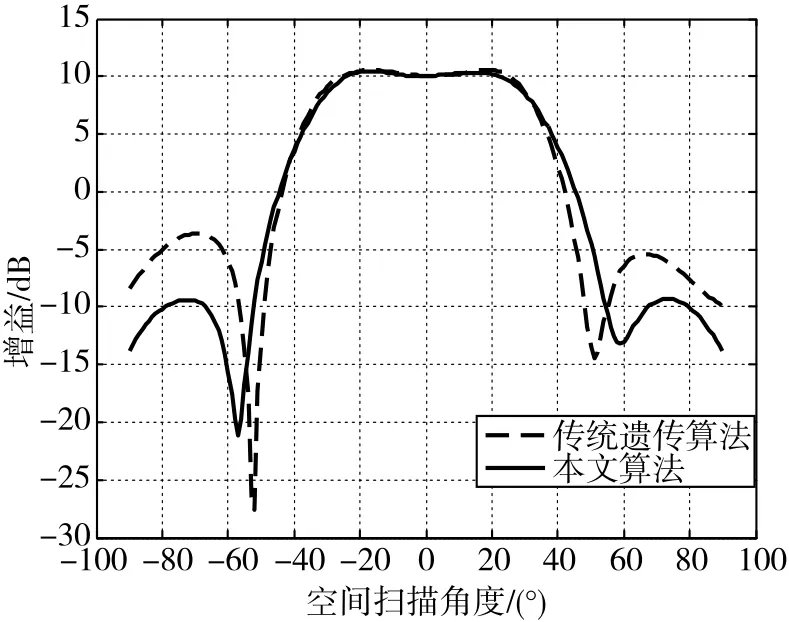
图6 中心波束赋形比较

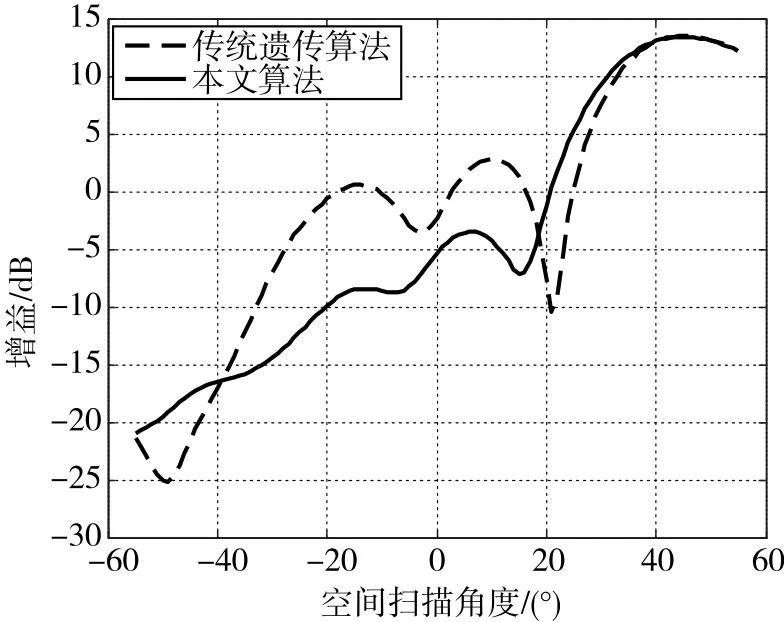
图7 边缘波束2赋形比较

采用本文算法依次对七个波束综合优化，得到相应幅相激励系数。合成的七个波束效果图如图8(a)所示，其等高线图如图8(b)所示。由图8(b)可以看出，波束间交叠增益低于主瓣区域增益1dB左右，边缘增益基本在12dB以上，满足系统指标要求。

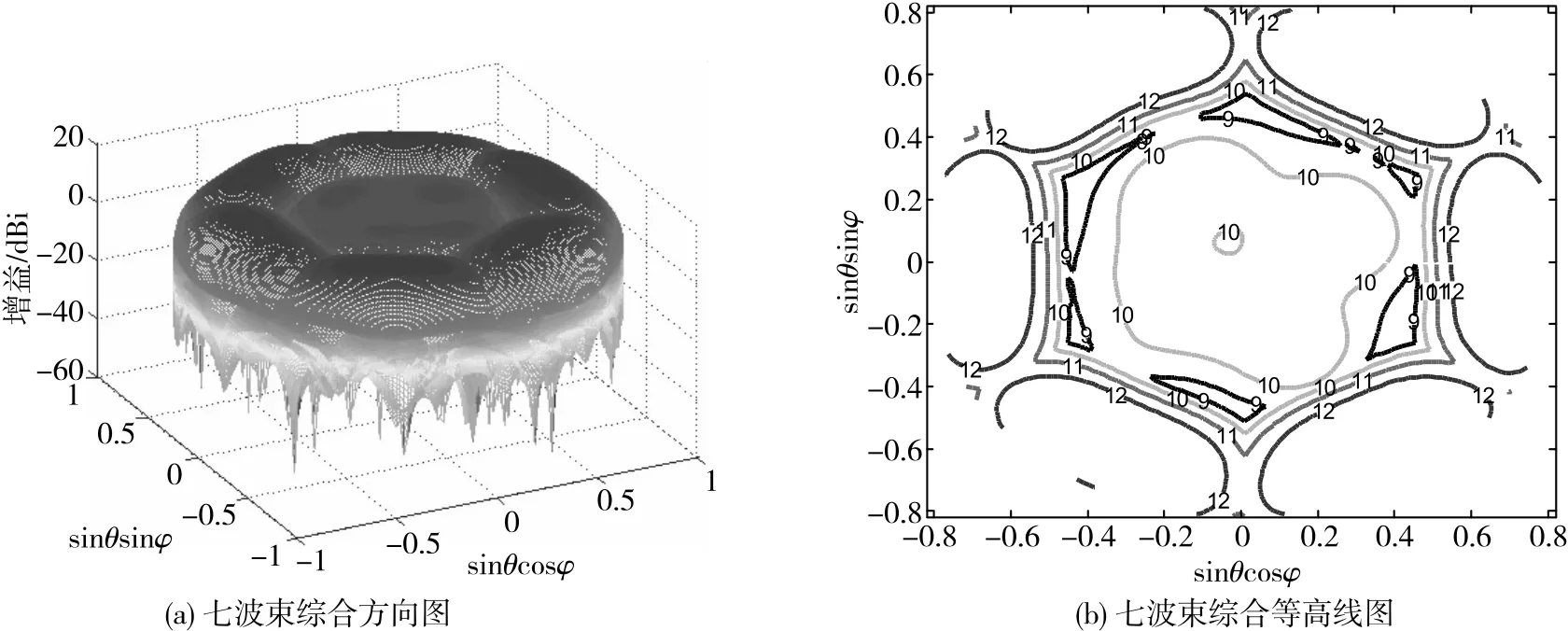
图8 七波束综合结果

对实际应用数字多波束系统做暗室测试，采用法国Satimo SG24 360°近场天线球面扫描系统测试19阵元平面阵接收天线的辐射方向图，测试时机械转动天线同时结合23个交叉极化探头扫描，利用软件计算天线的相关远场数据，得到完整辐射方向图。中心波束和边缘波束3的实测结果如图9所示。图9(a)和(c)分别为中心波束和边缘波束实测波束方向图，从图中可以看出，波束形状覆盖区域与设计区域吻合。图9(b)和(d)分别为中心波束和边缘波束中心截面图。其中，中心波束仿真俯仰角0°对应增益为10.29dB，旁瓣为－7.25dB，实测俯仰角0°对应增益为9.82 dB，旁瓣为－6.501dB；边缘波束仿真最大增益为12.93dB，旁瓣为－3.727dB，实测最大增益为12.95 dB，旁瓣为－4.352dB。比较仿真和实测结果可以看到，两者之间增益差异在1dB范围内，旁瓣抑制度均达到－15dB，认为实测结果符合仿真要求。

图9 波束实测结果

4 结束语

本文采用基于差分算子的遗传算法对19阵元平面阵天线方向图进行优化，结合七波束覆盖方案对各个波束进行特殊赋形。与传统遗传算法相比，本文算法通过引入差分进化算子，保持种群多样性，拓展了搜索空间，避免算法陷入局部收敛，改善了算法的收敛速度和寻优精度。本文还针对本征激励模式下的阵元方向图建立平面阵天线辐射模型，改进优化目标函数，保证了仿真模型的精度，提高了优化综合结果的实际性能。仿真与实测结果表明，本文算法能有效应用在平面阵天线方向图综合，具有广阔的应用前景。

[1] 余金培，杨根庆，梁旭文.现代小卫星技术与应用[M].上海：上海科学普及出版社，2004.

[2] 梁 广，贾铂奇，龚文斌.星载多波束相控阵天线等通量覆盖设计[J].电波科学学报，2010，25(2)：248～252.

[3] Liang Guang，Yu Jinpei，et al.Development of 61-channel Digital Beamforming(DBF)Transmitter Array for Mobile Satellite Communication[J].Progress In Electromagnetics Research(PIER)，97，2009：177～195.

[4] Liang Guang，Yu Jinpei，et al.A Semi-Physical Simulation System for DBF Transmitter Array on LEO Satellite[J]. Progress In Electromagnetics Research(PIER)，97，2009：197～215.

[5] 薛正辉，李伟明，任 武.阵列天线分析与综合[M].北京：北京航空航天大学出版社，2011.

[6] 尚 勇，梁 广，余金培，龚文斌.星载多波束相控阵天线设计与综合优化技术研究[J].遥测遥控，2012，33 (4)：37～41.

[7] Marcano D，Dur A N F.Synthesis of Antenna Arrays Using Genetic Algorithms[J].Antennas and Propagation Magazine，IEEE.2000，42(3)：12～20.

[8] Johnson J M，Rahmat-Samii V.Genetic Algorithms in Engineering Electromagnetics[J].Antennas and Propagation Magazine，IEEE.1997，39(4)：7～21.

[9] 梁 旭，黄 明.现代智能优化混合算法及其应用[M].北京：电子工业出版社，2012.

[10] 雷英杰，等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005：261.

[11] Storn R，Price K.Differential Evolution：a Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces[J].Technical Report，International Computer Science Institute，1995(8)：22～25.

参考文献

[1] Ndili.GPS Pseudolite Signal Design[C].Proceedings of the ION GPS，Salt Lake City，UT，September 1994.

[2] Stone J，LeMaster E，Powell J D，Rock S.GPS Pseudolite Transceivers and Their Applications[C].ION National Technical Meetings，San Diego，CA，January 25-27，1999.

[3] Van Dierendonck A J.GPS Ground Transmitters for Test Range Applications[C].ION GPS Conference，Colorado Springs，CO，September 1989.

[4] 谢 钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009.

[5] Cohen C，Pervan B，Cobb H S，Lawrence D，Powell J D，Parkinson B.Real-Time Cycle Ambiguity Resolution Using a Pseudolite for Precision Landing of Aircraft with GPS[C].Proceedings of the 2ndInternatonal Symposium on Differential Satellite Navigation Systems，Amsterdam，Netherlands，April 1993.

[6] Jianguo Jack Wang，Jinling Wang.Tropospheric Delay Estimation for Pseudolite Positioning[J].Journal of Global Positioning Systems，2005，Vol.4，No.1-2：106～112.

[7] Bouska C T J，Raquet J F.Tropospheric Model Error Reduction in Pseudolite Based Positioning Systems[C].ION GPS/GNSS 2003，Portland OR，USA，290～298.

[8] 乔仰文，等.GPS卫星定位原理及其在测绘中的应用[M].北京：教育科学出版社，2003.

[9] 刘基余.GPS卫星导航定位原理与方法[M].北京：科学出版社，2003.

[作者简介]

张如伟 1982年生，工程师，主要从事高精度卫星导航接收机软件算法设计与数据处理研究等工作。

黄晓瑞 1971年生，研究员，主要从事卫星导航领域研究工作。

李晓东 1968年生，研究员，主要从事卫星导航领域研究工作。

Application of Genetic Algorithm Based on Differential Evolution to Multi-beam Planar Array Antenna Synthesis

Zhang Renting， Liang Guang， Yu Jinpei

According to the multi-beam planar array antenna scanning with large angle utilized in LEO satellites，a modified genetic algorithm based on differential evolution is proposed to realize the array antenna synthesis of amplitude and phase coefficients.The genetic operator combined with differential evolution is adopted to generate the population.Therefore it is expected that the algorithm not only improves the convergence speed，but also optimizes results for synthesis.Simulations show that the pattern synthesis of planar antenna arrays can be carried out with optimized results reaching the designed goals.Simultaneously，the test results verify the accuracy of the planar array antenna radiation pattern and feasibility of the algorithm.

Multi-beam planar array antenna； Antenna synthesis； Genetic algorithm； Differential evolution

TN821.8

A

CN11-1780(2014)02-0053-07

章仁婷 1990年生，硕士研究生，主要研究方向为相控阵天线设计与综合优化技术。

梁 广 1983年生，博士，主要研究方向为相控阵天线技术、卫星通信技术。

余金培 1965年生，研究员，博导，主要研究方向为小卫星通信技术。

中科院创新基金项目(No.CXJJ-11-S107)；上海市自然科学基金(No.11ZR1435000)

2013-08-28 收修改稿日期：2013-11-05