一种纯伪卫星对流层延迟估计方法

张如伟， 黄晓瑞， 李晓东

(北京遥测技术研究所 北京 100076)

一种纯伪卫星对流层延迟估计方法

张如伟， 黄晓瑞， 李晓东

(北京遥测技术研究所 北京 100076)

伪卫星既可以作为全球导航卫星系统的增强系统，又可以作为一种独立的导航定位系统，在比较苛刻的观测条件下具有重要的应用意义。由于在一般应用中，伪卫星与接收机特殊的空间相对关系，使得对流层延迟成为伪卫星导航中一种重要的误差源，且与传统的全球导航卫星系统的改正方法有较大区别。参考诸多外文文献中提及的一种纯伪卫星对流层延迟估计方法，对方法进行相关改进，扩大了方法的应用范围，并进行了仿真验证。仿真结果表明，改进方法简单、准确、有效，且精度较高，可以应用于接收机处于任何仰角和高度情况下的纯伪卫星导航定位。

伪卫星； 对流层延迟； Hopfield模型

前言

伪卫星是安装在地面上、天空中或者舰船上的能发射类似于GPS信号的“卫星”[1～3]。常见全球导航卫星系统(GPS、GLONASS、Galileo、BD)的精确性、可靠性和可用性在一定程度上依赖于可跟踪卫星的数量以及几何分布情况，受这些因素的制约，在峡谷、室内、地下和超高空间(如火星)等比较苛刻的观测环境下，可视卫星的数量和几何布局无法满足定位操作的需求，而使用伪卫星可以解决这个问题。采用伪卫星技术对于帮助实现全球导航卫星系统定位的优势主要体现在两个方面：一是增加可见卫星的个数，提高定位效率；二是改善卫星的空间几何分布，减小PDOP值，提高定位精度[4]。此外，利用伪卫星还可以帮助确定卫星载波相位测量值的整周模糊度，从而实现精密定位[5]。伪卫星还可用来提高全球导航卫星系统的正直性，而多颗伪卫星还可以联合组成一个独立的定位系统，称为纯伪卫星导航定位系统。

与全球导航卫星系统类似，纯伪卫星导航定位系统在定位时也存在着大气延迟误差。然而在伪卫星应用中，由于接收机和伪卫星距离较近，且接收机高度有限，一般卫星仰角较低，大气延迟误差影响与传统的GPS相比具有较大的不同，需要采用不同的方法进行改正。这里，对流层延迟是伪卫星定位中主要误差源之一[6]。本文研究一种基于纯伪卫星的简单有效的对流层延迟估计方法，对提高纯伪卫星导航效率和精度具有较大意义。

1 纯伪卫星对流层延迟估计方法

对流层是高度约40km以下的大气层。较之电离层，对流层离地面更近，所以对流层中的大气密度远比电离层中的大，而且大气状态也会随着地面的气候变化而变化，这使得对流层折射比电离层更为复杂。对流层中的大气成分比较复杂，主要由氮和氧组成，同时还包含少量的水蒸气、二氧化碳、氢等气体。

一般来说，对流层折射延迟是一个关于大气参数、斜距(伪卫星与接收机)、高度角(接收机相对于伪卫星)的函数[7]。设对流层中的大气折射率为n，真空中的折射率为1，则对流层延迟Δtrop可写为

由于(n－1)数值很小，为方便计，令N＝(n－1)×106，N称为折射指数，可分为干气部分Ndry(约占90%)和湿气部分Nwet(约占10%)，即

在计算N时，诸多学者建立了多种由地面实验而得出的近似公式，各公式的常数略有出入，可无实质性的差别。其中干气部分与大气压P、绝对温度T有关，一般定义为

而湿气部分则和水汽压及绝对温度有关，一般定义为

式(4)中，f为相对湿度，取值0～1。

因此式(1)可写为

霍普菲尔德根据气象参数随高度变化规律和气态方程推导出折射指数在传播路径上变化的经验公式，即

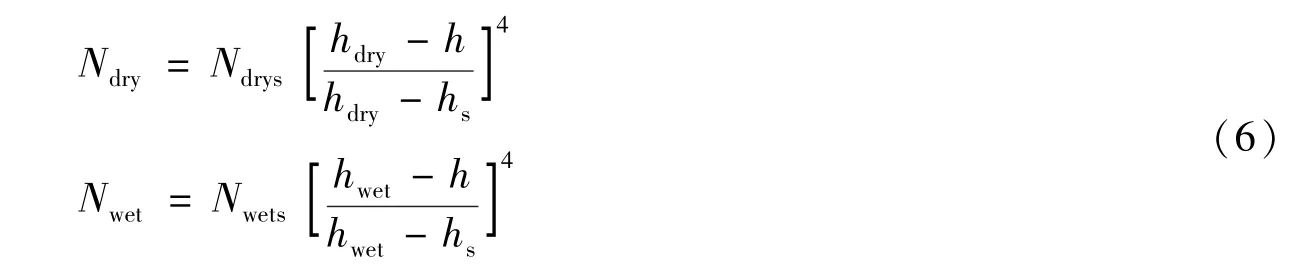
其中，Ndrys、Nwets为测站(测量大气参数站点)大气折射指数，hs为测站海拔高度，h为所求传播路径任意处高度，hwet、hdry为干湿大气层高度界线，分别定义为hwet＝12000m，hdry＝42700m。

根据式(5)和式(6)，积分可得信号传播路径上的对流层延迟。

文献[6，7]根据伪卫星信号传播特性，从霍普菲尔德模型上演绎出一种适合伪卫星对流层延迟的改正模型，对干、湿两部分延迟分别计算，即

式(8)、式(9)中，Rrov、hrov、hpl分别为伪卫星地面站与接收机的斜距、接收机高度、伪卫星地面站高度。该模型在整个仰角范围内(0°～90°)具有一定的优势，在与其他常用模型的比较过程中，其所体现的综合差异性最小，且适合负仰角应用[6，7]。

2 方法的局限性与改进

前述模型的优势使其成为针对伪卫星对流层延迟改正应用的一种比较好的方法，但该方法在应用范围上仍具有一定的局限性，下文将分别论述。

2.1 方法的局限性

①当伪卫星地面站与接收机高度相等时，该方法不适用。

当伪卫星地面站与接收机高度相等时，式(8)、式(9)中出现除数为零的现象，显然方法不再适用。

②当接收机高度穿越干、湿大气层分界线时，该方法不适用。

该模型虽是整个传播路径上的对流层延迟，但只适用于高度低于干、湿大气层分界线的情况，即当接收机高度分别穿越12000m、42700m时，式(8)、式(9)便不再适用。

2.2 方法的改进

①伪卫星地面站与接收机高度相等的情况。

当实际应用出现此类情况时，考虑到信号传播的可能性，一般接收机与地面站距离较近，此时我们可以近似假设两者气象参数相同，即大气折射指数N相同，这样可以不再考虑高度变化引起的大气折射指数变化，对式(5)进行积分计算得到对流层延迟。

式(10)中S即为地面站与接收机的直线距离，单位为m。

②接收机高度穿越干、湿大气层分界线的情况。

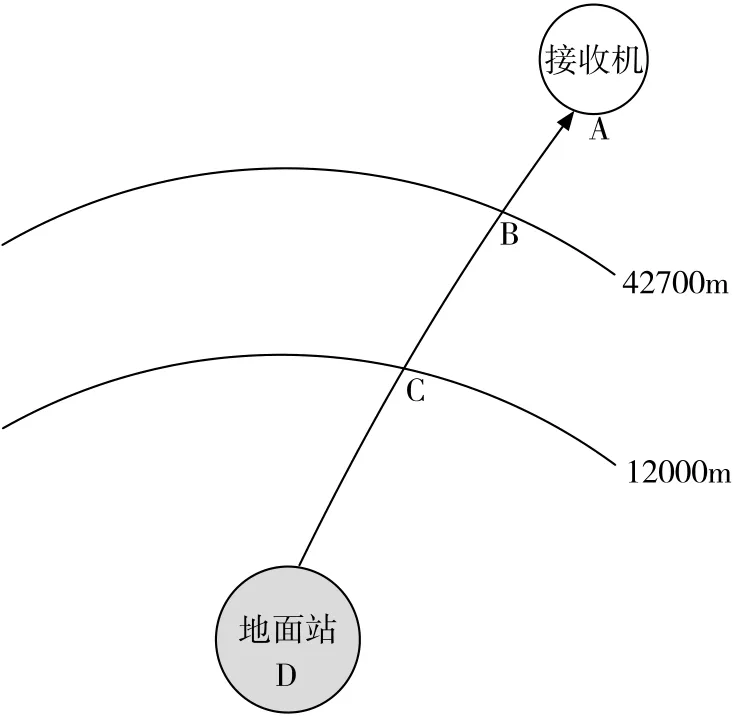
图1 接收机与地面站相对位置示意图

如图1所示，当接收机高度高于C点时，Nwet几乎为0，从C点到接收机的传播路径上湿部分对流层延迟几乎可以忽略不计；同样的道理，当接收机高度高于B点时，从B点到接收机的传播路径上干部分对流层延迟也几乎为0。因此，当接收机高度高于对流层湿、干分界线时，例如接收机位于图1中的A点，我们可以把地面站到接收机之间的对流层延迟归算到地面站到C点的湿部分延迟和地面站到B点的干部分延迟。根据以上想法，对式(8)、式(9)进行相应变换，以式(8)为例

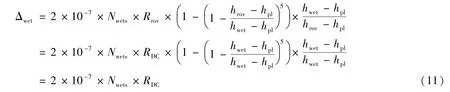
式(11)中RDC为地面站到C点的斜距。实际应用中，我们无法计算RDC的真实值，但是我们可以实时计算接收机本身的高程和与地面站的斜距，而这些参数存在以下等比关系

因此我们可以得到

“现在已经处于价格的底点，未来价格将稍有反弹并逐渐趋于平稳。”杨同宇认为，磷复肥会议结束后，许多肥料厂家已陆续出台了订肥政策。进入12月份，将进入生产、备肥的关键时期，需求将逐渐显现，并为市场提供支撑。

代入式(11)中，可得

同理可得

综合式(8)、式(9)、式(10)、式(14)、式(15)，我们可以得到任意应用条件下的伪卫星对流层延迟改正模型

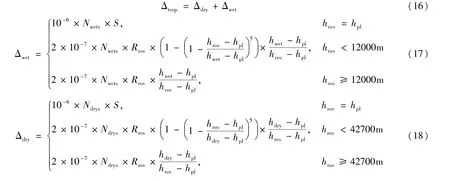
3 算例验证

为验证本文模型的正确性和有效性，特设计几个算例进行演算和分析。算例设计的基本思想是，利用常用的GPS对流层延迟改正模型间接计算伪卫星接收机对流层延迟，将其与利用本文模型计算的结果进行对比分析，从而验证本文方法的正确性和有效性。以计算图1中从伪卫星地面站到C点传播途径上的对流层延迟为例，我们可以分别计算位于地面站和C点的GPS接收机对流层延迟，两者相减即为待求值，然后将其与本文式(16)、式(17)、式(18)的计算结果进行对比分析。

算例的设计覆盖任意高度和仰角，包括零仰角和负仰角。本文中使用的GPS对流层延迟模型包括Hopfield模型和Saas tamoinen模型两个常用模型。同时，海平面上的标准气象元素设定为，温度15℃，气压1013.25mbar，相对湿度0.5。

3.1 算例1接收机高度分别为10km和30km伪卫星对流层延迟计算

为验证模型在任意高度的适用性，分别设计接收机高度在10km(低于大气层湿分界线)和30km(位于湿分界线和干分界线之间)两个算例，计算结果如图2和图3所示。

图2 接收机高度10km对流层延迟计算对比

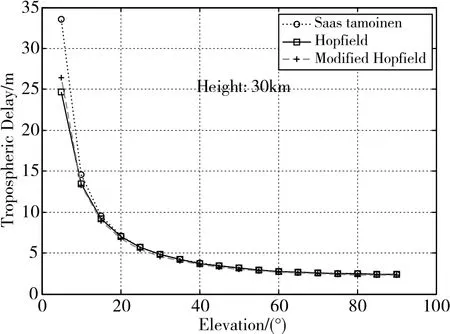
图3 接收机高度30km对流层延迟计算对比

图2和图3中的Modified Hopfield即为本文介绍的模型(以下类同)，图中结果覆盖接收机仰角0°～90°。由图可知，本文介绍的模型与Hopfield模型、Saas tamoinen模型计算结果在两个高度上吻合性都比较好，特别是在高仰角的情况下，三者相差在10cm左右；低仰角情况下三者相差较多，最大可达2m，由于Hopfield模型和Saas tamoinen模型在低仰角的情况下误差较大，特别是Saas tamoinen模型，其有效区间为10°～90°[8]，因此在低仰角情况下，模型精度不易评价。

3.2 算例2天顶方向40km以下对流层延迟计算

为验证不同高度天顶方向本文模型与其他两个模型的差别，特设计了40km以下天顶方向对流层延迟计算，计算结果如图4所示。

由图4可以看出，在整个高度范围内，三者结果吻合性都比较好，差别在0～10cm。在40km高处，本文模型计算出来的天顶方向对流层延迟约为2.3m，符合天顶方向整个对流层延迟约为2.3m～2.4m的真实情况[9]。

3.3 算例3仰角-90°～90°对流层延迟计算

为验证本文模型在所有仰角范围内的适用性，特设计该算例。在算例中，假设伪卫星高度在空中20km处，接收机位置在以伪卫星为圆心、半径为20km的圆上，则接收机高度最低为0km，最高为40km。计算结果如图5所示。

图4 40km以下天顶方向对流层延迟计算结果

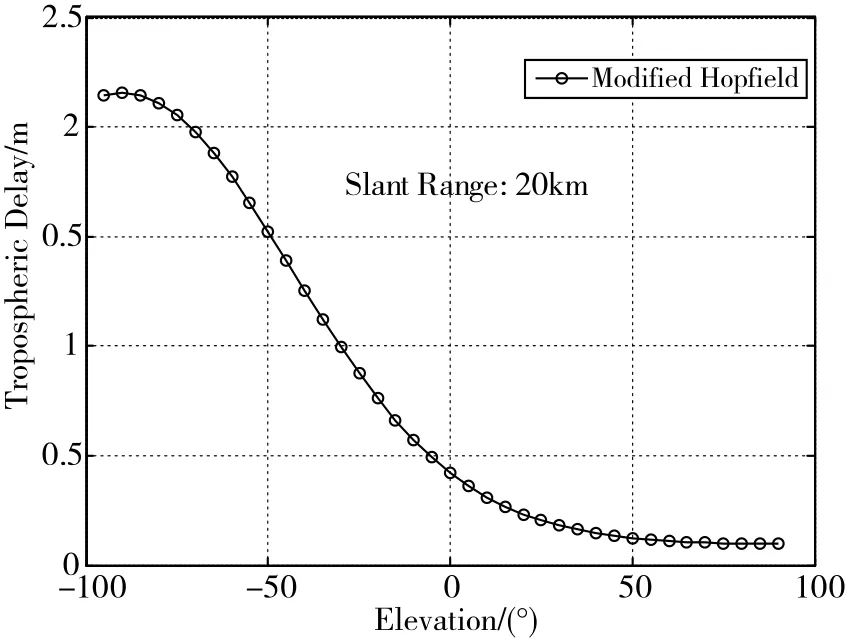
图5 仰角－90°～90°对流层延迟计算结果

图5中计算结果曲线平滑，证明了本文模型的有效性；在仰角为－90°时，即接收机位于海平面时，对流层延迟约为2.15m，在仰角为90°时，即接收机高度为40km时，对流层延迟约为0.1m，两者相加约为2.25m，与算例2中解算的0～40km天顶方向对流层延迟约为2.3m的结果基本吻合，证明了本文模型在负仰角使用情况下的准确性。特别需要指出的是，在0°高度角点，对流层延迟未出现跳跃现象，证明了该模型在0°仰角使用情况下的准确性。

3.4 算例4斜距为50km对流层延迟计算

该算例覆盖了仰角0°～90°、高度0～50km的测试范围，计算结果如图6所示。

从图6中可以看出，整个解算结果曲线平滑，在高度为50km处，对流层延迟为2.3m，与大气层分界线(42.7km)一致，证明本文模型适合于接收机高于大气层分界线任意高度的使用情况，且结果准确有效。

图6 斜距为50km对流层延迟计算结果

4 结束语

本文介绍了一种适合纯伪卫星的对流层延迟改正方法，并在原方法的基础上进行了分析和改进，通过设计算例证明改进后的模型适合接收机处于任意仰角和高度的使用场景，且精度较高，可在纯伪卫星导航工程中广泛应用。

[1] Ndili.GPS Pseudolite Signal Design[C].Proceedings of the ION GPS，Salt Lake City，UT，September 1994.

[2] Stone J，LeMaster E，Powell J D，Rock S.GPS Pseudolite Transceivers and Their Applications[C].ION National Technical Meetings，San Diego，CA，January 25-27，1999.

[3] Van Dierendonck A J.GPS Ground Transmitters for Test Range Applications[C].ION GPS Conference，Colorado Springs，CO，September 1989.

[4] 谢 钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009.

[5] Cohen C，Pervan B，Cobb H S，Lawrence D，Powell J D，Parkinson B.Real-Time Cycle Ambiguity Resolution Using a Pseudolite for Precision Landing of Aircraft with GPS[C].Proceedings of the 2ndInternatonal Symposium on Differential Satellite Navigation Systems，Amsterdam，Netherlands，April 1993.

[6] Jianguo Jack Wang，Jinling Wang.Tropospheric Delay Estimation for Pseudolite Positioning[J].Journal of Global Positioning Systems，2005，Vol.4，No.1-2：106～112.

[7] Bouska C T J，Raquet J F.Tropospheric Model Error Reduction in Pseudolite Based Positioning Systems[C].ION GPS/GNSS 2003，Portland OR，USA，290～298.

[8] 乔仰文，等.GPS卫星定位原理及其在测绘中的应用[M].北京：教育科学出版社，2003.

[9] 刘基余.GPS卫星导航定位原理与方法[M].北京：科学出版社，2003.

张如伟 1982年生，工程师，主要从事高精度卫星导航接收机软件算法设计与数据处理研究等工作。

黄晓瑞 1971年生，研究员，主要从事卫星导航领域研究工作。

李晓东 1968年生，研究员，主要从事卫星导航领域研究工作。

[7] Marcano D，Dur A N F.Synthesis of Antenna Arrays Using Genetic Algorithms[J].Antennas and Propagation Magazine，IEEE.2000，42(3)：12～20.

[8] Johnson J M，Rahmat-Samii V.Genetic Algorithms in Engineering Electromagnetics[J].Antennas and Propagation Magazine，IEEE.1997，39(4)：7～21.

[9] 梁 旭，黄 明.现代智能优化混合算法及其应用[M].北京：电子工业出版社，2012.

[10] 雷英杰，等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005：261.

[11] Storn R，Price K.Differential Evolution：a Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces[J].Technical Report，International Computer Science Institute，1995(8)：22～25.

[作者简介]

章仁婷 1990年生，硕士研究生，主要研究方向为相控阵天线设计与综合优化技术。

梁 广 1983年生，博士，主要研究方向为相控阵天线技术、卫星通信技术。

余金培 1965年生，研究员，博导，主要研究方向为小卫星通信技术。

A Tropospheric Delay Estimation Method for Pseudolite Positioning

Zhang Ruwei， Huang Xiaorui， Li Xiaodong

The pseudolite either as an enhanced system of global navigation satellite system，but also can be used as a standalone navigation system，has important applications on relatively harsh conditions of observation.In general applications，the special relative space relationship between pseudolite and receiver makes the tropospheric delay become an important error source，and the estimation method is quite different from the one for traditional global navigation satellite system.An estimation method of pseudolite tropospheric delay referred to in many foreign literatures is introduced and improved，and the improved method expands the application range.The simulation results show that the improved method is simple，accurate and effective，and it has high precision.The method can be applied to pseudolite positioning of any elevation and altitude situations.

Pseudolite； Tropospheric delay； Hopfield model

P228.4

A

CN11-1780(2014)02-0014-05

2013-12-04