宇宙空间演生与粘性宇宙

张 伟

(南昌大学理学院物理系，330031，南昌)

0 引言

人类对于时空的认识经历了漫长的发展过程。17世纪下半叶，牛顿(Newton)在前人研究的基础上，发表了万有引力定律，提出了绝对时空观。后来，爱因斯坦(Einstein)摒弃了牛顿的绝对时空观，提出了相对时空观。在爱因斯坦的广义相对论中，引力被描述为时空的弯曲而不再是作为自然界中一种基本的相互作用力，时间与空间都是相对的而且相互联系。广义相对论成功地经受了如引力红移、水星近日点进动和星光偏折等一系列观测与实验的检验，取得了极大的成功。然而，广义相对论没有考虑时空与物质的量子效应，是一个经典的理论。在广义相对论与量子论结合统一的过程中，人们遇到了极大的困难。广义相对论是一个不可重整化的理论，无法用量子场论的方法将引力量子化。这些事实都迫使我们不得不去对时空的本质进行更深层的探索。

20世纪70年代，Bekenstein和Hawking等发现了黑洞的热力学性质[1－3]。黑洞具有正比于其视界面积的熵，而黑洞的温度正比于黑洞视界的表面引力。后来，Jacobson[4]从基本的热力学关系出发推导出了Einstein场方程，提出了Einstein场方程的热力学描述。2010年，E Verlinde[5]在全息原理的基础上，提出引力是熵力，而熵力是由与物体位置相关联的信息的改变而产生的一种有效的宏观力。从而进一步发展了引力不是基本相互作用力的观点。最近，T Padmanabhan[6]提出一个时空观点:宇宙空间是随着宇宙时间的发展而演生出来的，宇宙空间的膨胀率归因于全息视界面的自由度数与主体的自由度数之差。由此假设出发，T Padmanabhan成功地推导出了描述宇宙演化的Friedmann方程。然而，在真实的宇宙中，粘滞效应对于宇宙的演化将会带来不可忽略的影响。所以，当考虑到宇宙的粘滞效应时，T Padmanabhan的宇宙空间演生的理论是否依然能够有效的描述宇宙的演化规律?

本文首先将简要回顾T Padmanabhan提出的时空理论，然后在此基础上，将T Padmanabhan的工作推广到粘性宇宙的情况，并成功得到描述粘性宇宙演化规律的Friedmann方程。本文采用自然单位制，其中ħ=c=kB=1。

1 T Padmanabhan理论的回顾

首先，T Padmanabhan的宇宙空间演生的理论思想可用图1来演示。图1中球体内部区域是随着宇宙时间t的发展而已经演生出来的宇宙空间，并且宇宙空间体积的膨胀规律遵从图1中右上角所示的方程。

考虑一个纯的德西特(de Sitter)宇宙，该宇宙所遵循的全息原理可用以下关系式描述

其中Nsur和Nbulk分别表示全息视界面和主体的自由度数。全息视界面的半径为哈勃半径H－1，H=/a为哈勃参数。因此

将式(2)、式(3)代入式(1)，并利用 p= －ρ，可得

与标准结果一致。

然而，世界不是纯的而是渐进德西特宇宙。于是可以猜想宇宙体积的膨胀率与(Nsur－Nbulk)有关

将式(2)、式(3)代入式(5)，得到标准的动力学Friedmann方程

利用连续性方程

并且对方程(6)积分，可得标准的运动学Friedmann方程

上式中已令积分常数为零。

2 将T Padmanabhan的理论推广到粘性宇宙

不失一般性，考虑粘性Friedmann-Robertson-Walker(FRW)宇宙，其度规如下

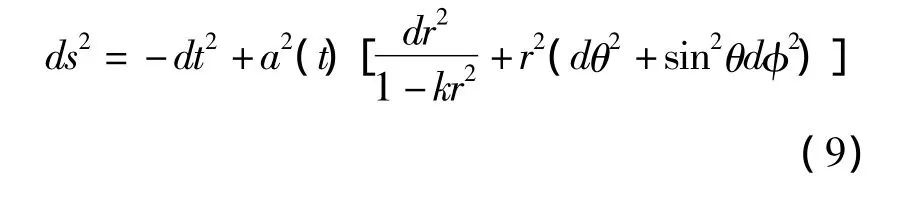
其中，k=1，0，－1分别对应封闭、平坦、开放的粘性FRW宇宙。

粘性 FRW 宇宙的能动张量[7－9]为

其中，体粘滞系数ξ为流体的能量密度ρ的函数。由于要遵循热力学第二定律，所以体粘滞系数应为正值。

为了将T Padmanabhan的宇宙空间演生的理论推广到粘性宇宙的情况，把式(2)、式(3)代入实现其理论思想的核心方程式(5)，则

现在，欲从式(11)出发推导出描述粘性宇宙演化规律的Friedmann方程，最关键的问题是要得到粘性FRW宇宙的Komar质量M。

在广义相对论中，导致宇宙加速膨胀的不是宇宙空间区域的物质的总质量，而是所谓的有效引力质量-即Komar质量。粘性FRW宇宙的Komar质量的表达式为[10，13]

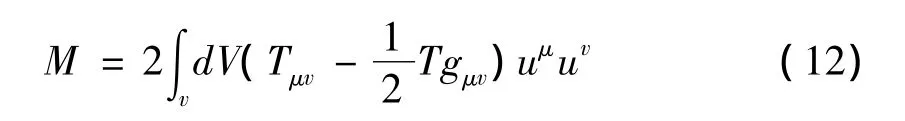
为此，先求出能动张量Tμv的迹T的表达式

再将式(10)、式(13)代入式(12)，则

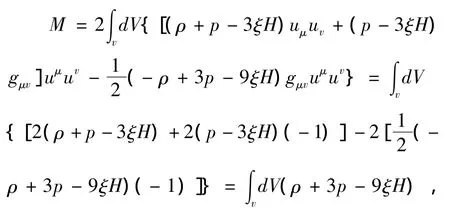
即得粘性FRW宇宙的Komar质量的具体表达形式为

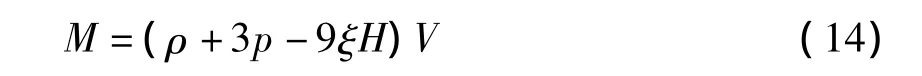
再将式(14)代入式(11)，有

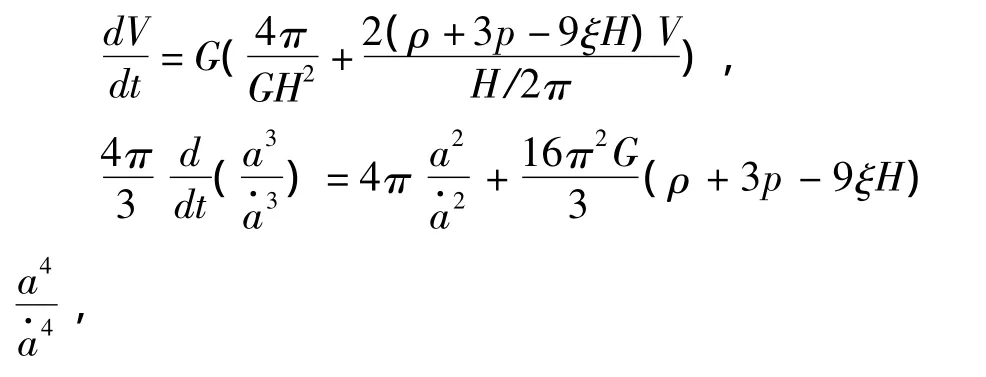
化简，得

式(15)是用T Padmanabhan的宇宙空间演生的时空理论推导出的粘性FRW宇宙的动力学Friedmann方程，将其与粘性FRW宇宙的标准的动力学 Friedmann 方程[8－9]对比，发现二者相同。接下来从式(15)出发，利用连续性方程，看能否推导出粘性FRW宇宙的标准的运动学Friedmann方程。

首先，粘性FRW宇宙的连续性方程▽μTμv=0 成为[7－9]

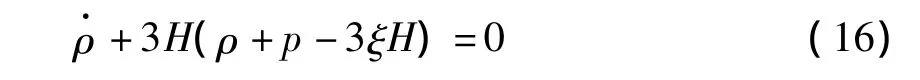
由式(16)，得

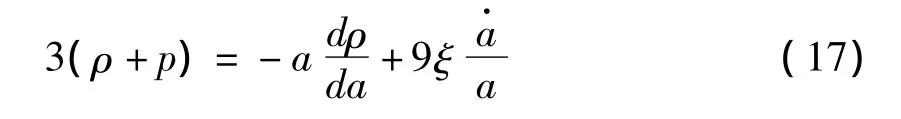
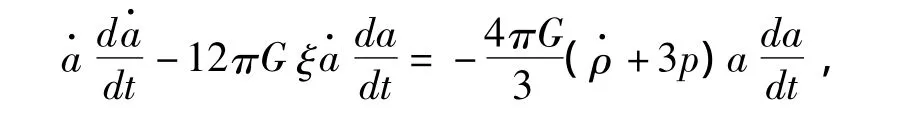
再将变形后的连续性方程(17)代入上式

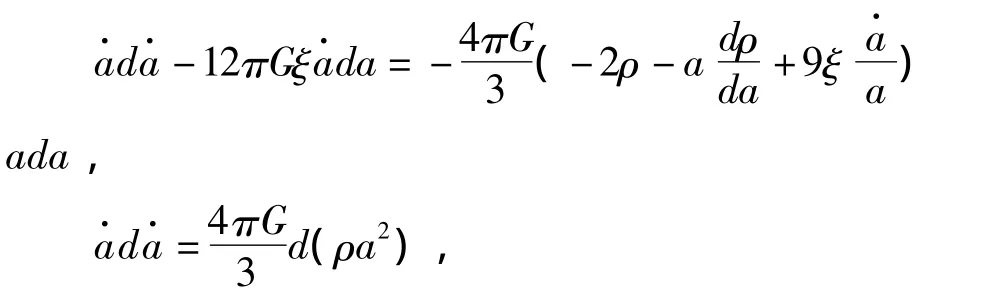
对上式两边同时积分并令积分常数为零

即

将式(18)与粘性FRW宇宙的标准的运动学Friedmann方程[8－9]对比，发现二者相同。可见，用T Padmanabhan的宇宙空间演生的时空理论能够成功地推导出描述粘性FRW宇宙的演化规律的Friedmann方程。

3 结论

本文采用T Padmanabhan的时空观点，认为宇宙空间是随着宇宙时间的发展而演生出来的，并且宇宙空间的膨胀率归因于全息视界面与主体的自由度数之差。继而成功地将T Padmanabhan的工作推广到粘性FRW宇宙的情形，所得结果与标准的Friedmann方程完全相同。进一步验证了T Padmanabhan的建立在全息原理基础上的时空观点的正确性。

另外，虽然在文中考虑的是粘性FRW宇宙，但是，由于描述宇宙粘性的体粘滞系数在宇宙中实际上起到一个等效压强的作用，所以，对于其它的宇宙学模型[11－13]如膜宇宙、标量-张量宇宙和 f(R)宇宙等，相信当在这些修正的引力的宇宙中考虑粘性时，仍然可以得到相应情况下的标准的Friedmann方程。

空间均匀且各向同性的FRW宇宙学模型有效的描绘了当今大尺度结构的宇宙。然而，对于早期的宇宙来说，其空间均匀却各向异性，需要用Bianchi型的宇宙学模型来描述。因此，如何将宇宙空间演生的理论推广到早期宇宙的情况是一个值得思考而又有趣的问题。因为，当考虑Bianchi型的宇宙学模型时，如何选取全息面从而能够运用建立在全息原理基础上的宇宙空间演生的理论是一个需要克服的困难。这些问题都有待于将来进一步的探索。

[1] Bekenstein J D.Black holes and entropy[J].Phys Rev D，1973，7:2333 －2346.

[2] Hawking S W.Particle creation by black holes[J].Commun Math Phys，1975，43:199 －220.

[3] Bardeen J M，Carter B，Hawking S W.The four laws of black hole mechanics[J].Commun Math Phys，1973，31:161－170.

[4] Jacobson T.Thermodynamics of spacetime:the einstein equation of state[J].Phys Rev Lett，1995，75:1260 －1263.

[5] Verlinde E.On the origin of gravity and the laws of newton[J].Jhep，2011，1104:029.

[6] Padmanabhan T.Emergence and expansion of cosmic space as due to the quest for holographic equipartition[J].arXiv:1206.4916v1[hep-th].

[7] Li W J，Ling Y，Wu J P，et al.Thermal fluctuations in viscous cosmology[J].Phys Lett B，2010，687:1 －5.

[8] Cataldo M，Cruz N，Lepe S.Viscous dark energy and phantom evolution[J].Phys Lett B，2005，619:5 －10.

[9] Brevik I，Gorbunova O，Saez-Gomez D.Casimir effects near the big rip singularity in viscous cosmology[J].Gen Rel Grav，2010，42:1513 －1522.

[10] Cai R G，Cao L M，Ohta N.Friedmann equations from entropic force[J].Phys Rev D，2010，81:061501(R).

[11] Cai R G，Kim S P.First law of thermodynamics and friedmann equations of friedmann-robertson-walker universe[J].Jhep，2005，0502:050.

[12] Cai R G，Akbar M.Friedmann equations of FRW universe in scalar-tensor gravity，f(R)gravity and first law of thermodynamics[J].Phys Lett B，2006，635:7－10.

[13] Ling Y，Pan W J.Note on the emergence of cosmic space in modified gravities[J].Phys Rev D，2013，88:043518.