复合整函数的有理零点

吴渊鸿，涂 金

(江西师范大学数学与信息科学学院，330022，南昌)

1 引言和结果

本文使用值分布理论中的标准记号[1]，用ρ(f)表示亚纯函数f(z)的增长级，并用σ2(f)表示亚纯函数f(z)的超级，定义如下[2]

本文用f(g)表示2个整函数f(z)与g(z)的复合，当然f(z)也可以为亚纯函数。关于复合整函数的不动点，很多人都进行了研究，并取得了很多有名的结果。

Gross猜测2个超越整函数的复合f(g)有无穷多个不动点[3]，当 f(g)为有穷级时，或者 f，g中有一个为多项式时，这个猜测被证明是对的。Yang C C.在他的2篇论文中分别证明了下面的定理。

定理 1[4]:假设 F(z)=f(g(z))是一无穷级的复合整函数，f的级ρ(f)小于或者为无理数，g满足

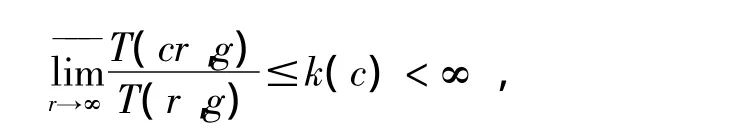
这里c＞1为一常数，则F=g(f)有无穷多个不动点。

定理2[5]:假设g(z)是一有穷级整函数，且具有一有穷的Borel例外值。f(z)是一非线性的整函数，使得f(g)的超级小于g的级，则F=f(g)有无穷多个不动点。

1990年，W Bergweiler证明了更一般的情况，得到以下定理。

定理 3[6]:假设 f，g 为超越整函数，P 是非常数多项式，那么f(g)-P有无穷多个零点。

那人们自然会问:当f为亚纯函数时，是不是有类似的结论?1993年W Bergweiler证明了下面这个定理。

定理 4[7]:假设 f为超越亚纯函数，g 为超越整函数，R是非常数有理函数。如果f(g)是无穷级的，那么f(g)-R有无穷多个零点。

本文在f，g为超越整函数，R为有理函数的条件下，研究了f(g)-R的零点，得到了以下定理，完善了上面几个定理的结果。

R为有理函数，则f(g)-R有无穷多个零点。

定理6:假设f为超越整函数，g为有穷级超越整函数，使得f(g)的超级小于g的级。R为有理函数，则f(g)-R有无穷多个零点。

2 引理

引理1[8]:假设 f，g 均为整函数，那么对于 r＞0有

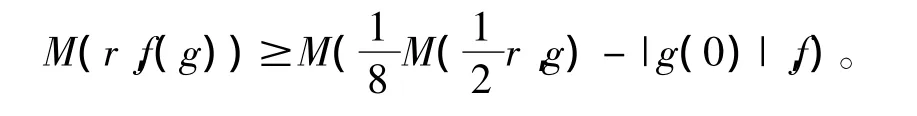
引理2[4]:假设f(z)为一有穷级的亚纯函数，g为一整函数满足

其中，c＞1为常数。如果对于整函数α，有

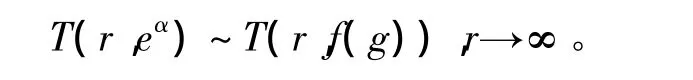
那么有:

其中，E是一个测度为有限的集合。

引理 3[9]:假设 F0，F1，…，Fm是 m+1 个不恒等于零的亚纯函数，g为非常数的整函数，h0，h1，…，hm是m+1个亚纯函数，K＞0是一绝对常数，使得

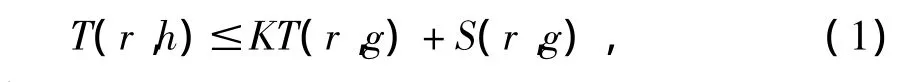
其中，当g为有穷级时，S(r，g)=O{log r};当 g为有无级时，S(r，g)=O{log(rT(r，g))}，至多除去一个测度为有限的集合E。如果

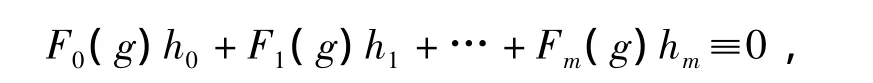
那么，存在多项式 Q0，Q1，…，Qm，使得

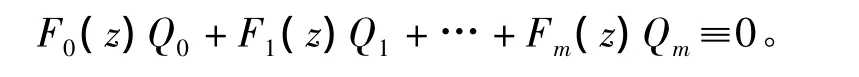
注:从文献[9]中的证明可知当g为有穷级时，只需一无界的非减正数序列{rj}∞j=1使得式(1)成立，引理的结论依然正确。

3 定理1的证明

假设f(g)-R有穷多个零点，则有

其中，R1是理函数，且每次出现不必相同，α是一整函数。由于f(g)为无穷级整函数，R1为有理函数，由式(2)有

对式(2)两边求导，有

由式(2)和式(4)，得到

+α')R －R'，由式(3)和引理2，有

其中，E是一个测度为有限的集合。由引理3知道，存在多项式 Q0，Q1，Q2，使得

由文献[9，10]可知，任何一阶代数微分方程的超越解的增长级必为正有理数且≥，由此可得方程(6)的整函数解的增长级为有理数且≥，这与定理的假设矛盾，故f(g)-R有无穷多个零点。

4 定理2的证明

假设f(g)-R有穷多个零点。则有

其中:R1为有理函数;α是一整函数。类似定理1的证明可以得到

其中，r0＞0为一固定常数，从而

即α的级不超过f(g)的超级，所以α，α'的级均小于g的级。因此，可以找到一无界的非减正数序，使得

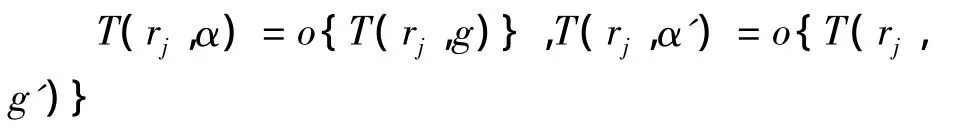
而g为有穷级超越整函数，故由引理3及其注，存在不全为零的多项式 Q0，Q1，Q2，使得

那么由定理1中同样的证明，可以得出矛盾。故f(g)-R有无穷个零点。

[1] 杨乐.值分布论及其新研究[M].北京:科学出版社，1982.

[2] 仪洪勋，杨重骏.亚纯函数唯一性理论[M].北京:科学出版社，1995.

[3] Gross F.Factorization of Meromorphic Functions[M].Washington D.C:U.S.Government Printing Office，1972.

[4] Yang C C.On the fixed－points of composite transcendental entire functions[J].J Math Anal Appl，1985，108(2):366－ 370.

[5] Yang C C.Further results on the the fixed－points of composite transcendental entire functions[J].J Math Anal Appl，1982，90:259 －269.

[6] Bergweiler W.Proof of a conjecture of Gross concerning fix－points[J].Math Z，1990，204:381 －390.

[7] Bergweiler W，Yang C C.On the value distribution of composite meromorphic functions[J].Bull London Math Soc，1993，25:357 －361.

[8] Clunie J.The composition of entire and meromorphic functions，Mathematical essays dedicated to A[J].J Macintyre Ohio Press，Athens，Ohio，England，1970:75－92.

[9] Steinmetz N.Uber die Faktorisierbaren Lösungen gewöhnlicher Differential gleichungen[J].Math Z，1980，170:169－180.

[10] Valiron G.Sur les fonctions entières vèrifiant une class d'équations différentielles[J].Bull Soc Math France，1923，51:33 －45.