Marcinkiewicz积分的弱(1，1)有界性

金芳婷

(江西师范大学数学与信息科学学院，330022，南昌)

1 主要结果

受文献[1－2]算子核条件的启发，介绍一种满足新的核条件的Marcinkiewicz积分，假设K∈L2(Rn)，存在常数 c＞0，使得

1)对所有 x，y∈Rn，有

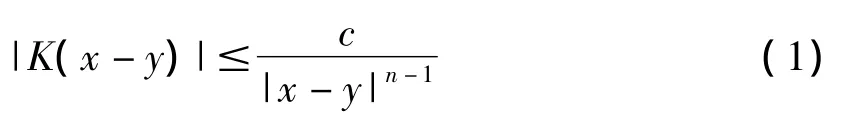
2)对于固定的 γ ＞0，对所有 x，y∈Rn，有

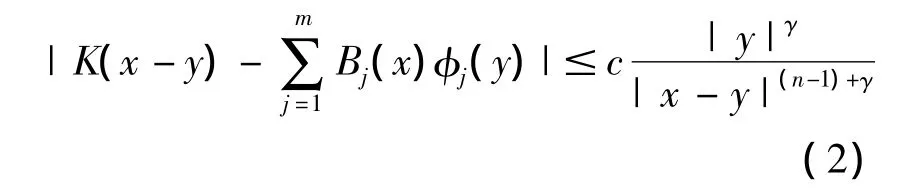
3)存在函数 B1，…，Bm∈(Rn{0})和{φ1，…，φm}⊂L∞(Rn)，使得

设f∈L1(Rn)，定义相应于K的Marcinkiewicz积分

[3]的部分方法可证明如下定理。

定理1:设μφ是由式(3)定义的Marcinkiewicz积分，K满足1)～3)，且它在Lp0(Rn)上有界，则存在常数c＞0，使得对所有的λ＞0和f∈L1(Rn)，有

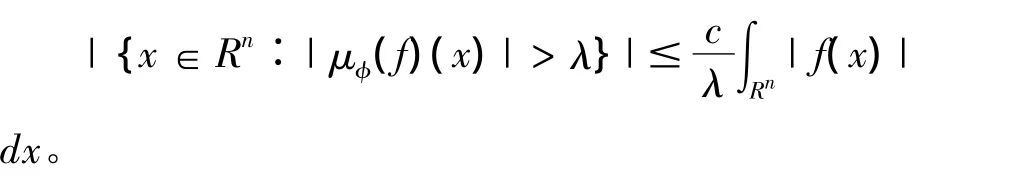
2 预备知识和引理

回忆投影的概念[4]，函数f∈L1在有限子空间Y(⊂L1)上的投影P(f)是指存在元素P(f)∈Y ，使得对任意的函数h∈Y，有

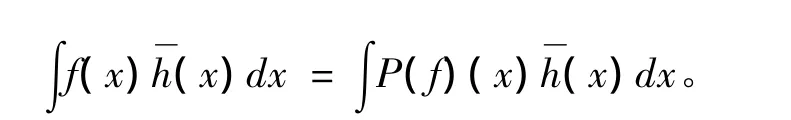
引理1[4]:设φ1，…，φm是定义在Rn上的一组有界函数且 |det[φr(yi)]|2∈ RH∞(Rnm)，则对于任意中心在原点的方体Q和任意的f∈L1(Q)，存在f在spanφ1，…，φm⊂L1(Q)上的投影PQf且满足

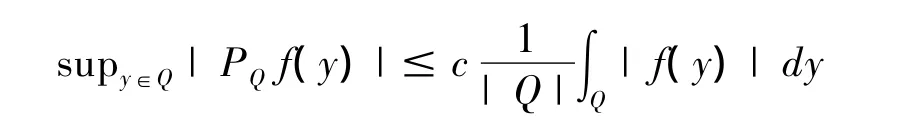
其中常数 c依赖于 n，m 和|det[φr(yi)]|2的RH∞常数。

3 定理的证明

定理1的证明:对于任意固定的λ＞0，考虑f的Caldero'n－Zygmund分解，得到一列互不重叠的方体 Qj，其中 Qj=Q(yj，rj)以 yj为中心 rj为半径，进一步有

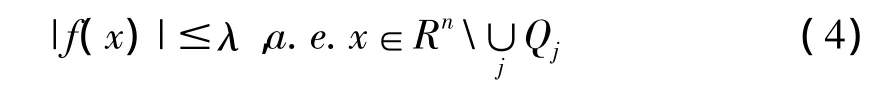
且对每个Qj有

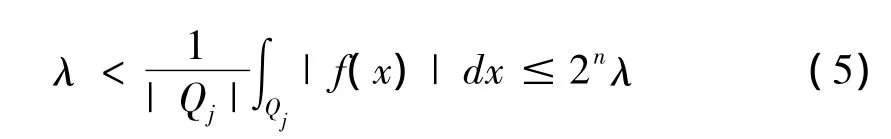
记f|Qj为函数f在 Qj上的限制，gj(x)为 f|Qj在 spanφ1(· －yj)，…，φm(· －yj)中的投影，把函数f分解为f=g+b，其中

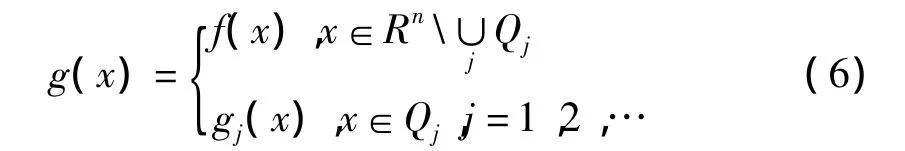
且

这里

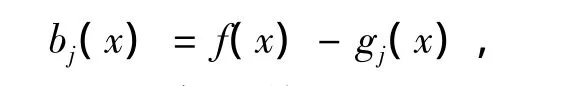
当 x ∈ Qj时，显然 supp

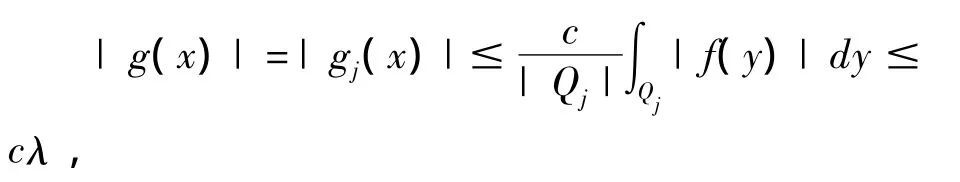
从而

进一步还可以验证

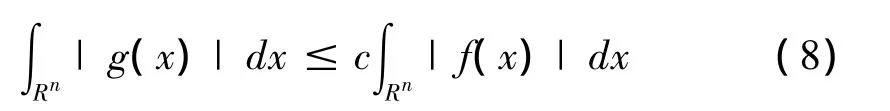
事实上，由引理1得

对于 I1，P0＞1，由 μφ在 Lp0(Rn)上有界，式(7)和式(8)，有

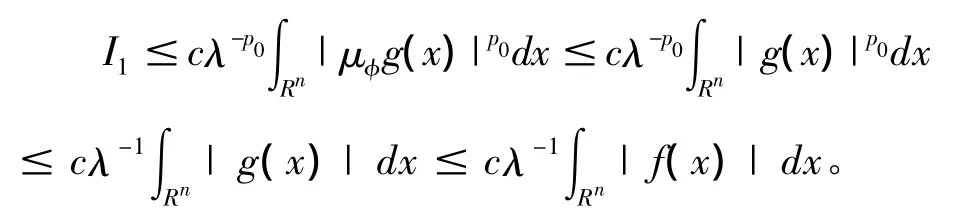
对于I2，由式(5)得

下面估计I3，注意到

因此，只需证明对于每一个固定的j，

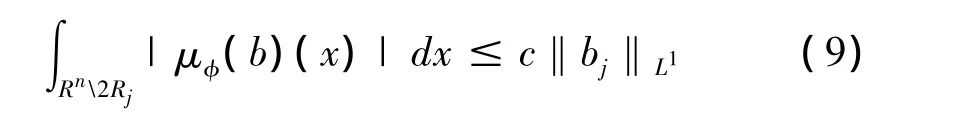
和

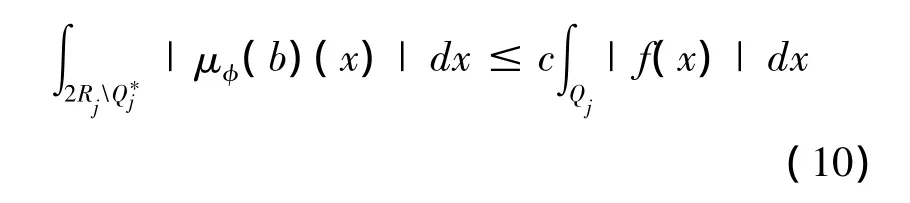
为证明式(9)，对每一个固定的j，有

由Minkowski不等式和式(1)可得

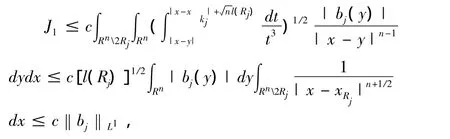
综合J1，J2的估计就得到式(9)。

为了证明估计式(10)，首先注意到如果对某个方体I，supp(h)⊂ I，那么对任意s＞ 1和x∉sI，由式(1)

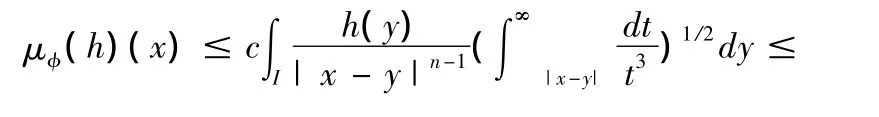
另一方面，有

因此，由上两式及supp(bj)⊂Qj，有

这就得到式(10)的估计，便可完成定理1的证明。

参考文献:

[1] Grubb D J，Moore C N.A variant of Hörmander's condition for singular integrals[J].Colloq Math，1997，73(2):165－172.

[2] Tolsa X，BMO.H1Calderón－Zygmund operators for non doubling measures[J].Math Ann，2001，319:89 －149.

[3] Tolsa X.A proof of week(1，1)inequality for singular integrals with non doubling measures based on a Calderón－Zygmund decomposition[J].Publ Mat，2001，45:163－174.

[4] Trujillo－Ginzález R.Weighted norm inequalities for singular integral operators satisfying a variant of Hörmander's condition，Comment[J].Math Univ Carolinae，2003，44(1):137 －152.