收敛性、闭性与拓扑空间
李云霞,刘高杰,周 琴
(成都理工大学 管理科学学院,四川 成都 610059)
1 拓扑空间和闭集
定义1 设X 是一个集合,T 是X 的一个子集族.如果T 满足以下条件:
①X,φ ∈T;
②若A,B ∈T,则A ∩B ∈T;
③若T1⊂T,则∪A∈T1A ∈T.
则称T 是X 的一个拓扑.
如果T 是集合X 的一个拓扑,则称偶对(X,T)是一个拓扑空间,或称集合X 是一个相对于拓扑T而言的拓扑空间;或者当拓扑T 早已约定或在行文中已有说明而无需指出时,称集合X 是一个拓扑空间.此外,T 的每一个元素都称为拓扑空间(X,T)(或X)中的一个开集.
定义2 设E ⊂Rn,如果E 的每一个聚点都属于E,则称E 为闭集.
引理1 设X 是一个拓扑空间,A ⊂X,则A 是一个闭集当且仅当A 的补集A' 是一个开集.
证明
1)必要性.
2)充分性.
设A'是一个开集.如果x ∈A',则A'是x 一个邻域,它满足条件,A' ∩A = φ.因此,xd(A).于是有d(A)⊂A,即A 是一个闭集.
定理1 设X 是一个拓扑空间,记Ψ 为所有闭集构成的族,则:
①X,φ ∈Ψ;
②如果A,B ∈Ψ,则A ∪B ∈Ψ,从而如果A1,A2,…,An∈Ψ,n ≥1,则A1∪A2∪…An∈Ψ;
③如果φ ≠Ψ1⊂Ψ,则∩A∈Ψ1A ∈Ψ.
证明 根据引理1 有,Ψ = {U' | U ∈T},其中,T 是X 的拓扑.
1)由于X,φ ∈T,所以,
φ = X',X = φ' ∈Ψ.
2)当时A,B ∈Ψ,有A',B'∈T,从而A'∩B'∈T.因此,
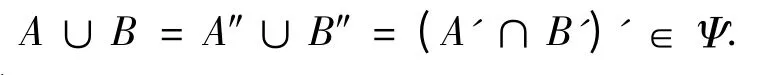
3)令T1= {A| A' ∈Ψ1},于是T1⊂T,因此∪U∈T1U ∈T.从而,

由定理1 知,可用定义闭集的方式来确定拓扑结构.
2 收敛性、闭性与拓扑空间
2.1 度量空间中的收敛性与闭性
设(X,d)为度量空间,d 是距离,定义,

为x0的以ε 为半径的开球,亦称为x0的ε-邻域.
设{xn}是(X,d)中的点列,如果存在x ∈X,使则称点列{xn}是(X,d)中的收敛点列,x 是点列{xn}的极限.类似于Rn,可以证明度量空间中收敛点列的极限是唯一的.
类似于Rn,可以证明度量空间中收敛点列是有界点集.度量空间中闭集也可以用点列的极限来定义.
定理2 M 是闭集的充要条件是M 中任何收敛点列的极限都在M 中,即若xn∈M,n = 1,2,…,xn→x,则x ∈M.
证明 必要性显然成立.由定义易知M 的每个聚点都属于M,从而M 是闭集.
2.2 收敛性和闭集
定义3 设X 是一个非空集合,XS是由X 上的所有点列构成的集合,若XS× X 的子集S,满足:对任意α,β ∈XS,若(α,x)∈S,且β 是α 的子列,则(β,x)∈X,则称S 是集合X 上的一个收敛.此时(α,x)∈S 可称为点列α 在X 中收敛于x,或称x 为点列α 的极限,记为
定义4 设X 是一个非空集合,S 是集合X 上的一个收敛,A ⊂X.若A 中的收敛点列的极限仍属于A,则称A 为X 在S 下的闭集.
定理3 设X 是一个非空集合,S 是集合X 上的一个收敛.记Ψ 为X 在S 下的全体闭集构成的集族,则:①φ,X ∈Ψ;②若A,B ∈Ψ,则A ∪B ∈Y;③若Ψ1∈Ψ,则F ∈Y.
证明 根据定义4,得:
1)显然成立φ ∈Ψ.对A ⊂X,若A 中的收敛点列的极限仍属于A,收敛点列仍在X 中,其极限也属于X,故有X ∈Ψ.
2)若A,B ∈Ψ,任取A ∪B 中的点列{xn}其收敛于x,则其在集合A 中{xn}的子列也收敛于x,由于A 是闭集,故x ∈A;在集合B 中{xn}的子列也收敛于x,由于B 是闭集,故x ∈B;从而x ∈A ∪B,于是A ∪B ∈Ψ.
3)任取F 中的点列{xn},其收敛于x,由于F 是闭集有x ∈F,又因为{xn}⊂F,所以{xn}F.于是由x ∈F 可得因此
定理4 记TS= {U ⊂X| U'∈Ψ},则TS是X上的一个拓扑.
证明 Ψ 满足定理3 的3 个条件,故TS满足定义1 的3 个条件,因而TS是X 上的一个拓扑.
定理4 说明,由集合X 上的收敛S 可赋予X 一个拓扑结构TS.
例1 设X 是一个平庸空间,XS是由X 上的所有点列构成的集合,取S = XS× X,易知S 是X 上的一个收敛,由定义4 可知平庸空间X 也是个闭集,从而平庸空间X 上的收敛S 赋予X 一个拓扑结构,称之为平庸拓扑.
例2 设X 是一个离散空间,XS是由X 上的所有点列构成的集合,由于X 中的每个集合都是开集,即有A ⊂X,A'⊂X.根据引理1 知,A 是闭集.从而令S = {({xn},x)}存在M ∈Z+,使得当n >M 时,有xn≡x},易知S 是X 上的一个收敛,由定义4 可知离散空间X 也是个闭集,从而离散空间X 上的收敛S赋予了X 一个拓扑结构,称之为离散拓扑.
定义5 设{xi}i∈Z+是拓扑空间(X,T)中的一个序列,x ∈X.如果对于x 的每一个领域U,存在M∈Z+使得当i >M 时有xi∈U,则称点x 是序列{xi}i∈Z+在拓扑T 下的一个极限点(或极限),也称为序列{xi}i∈Z+收敛于x,记作
如果序列至少有一个极限,则称这个序列是一个收敛序列.
需要指出的是,(X,TS)中的S 收敛与TS收敛可能不一致.
例3 设X 是一个不可数集,T 是X 上的可数补拓扑.可以证明X 中的一个点列{xn}拓扑T 收敛于x的充要条件是,存在M ∈Z+使得当i >M 时xi= x.若X 上的拓扑T 是X 上的某个收敛S 确定的拓扑.即,存在X 上的收敛S,使得TS= T.
可证,X 上的点列{xn}的T 收敛与S 收敛一定不一致.这是因为,若两种收敛是一致的,则由上述定义知,{xn}S 收敛于x,当且仅当,存在M ∈Z+使得当i >M 时xi= x.而(X,TS)(= (X,T))中的子集A 是闭集,当且仅当,若{xn}⊂A,并且{xn}S 收敛于x,则必有x ∈A.
因为TS= T,即TS是可数补拓扑,故对于A 真包含于X:A 是闭集,当且仅当,A 是可数集.取B 是X 的一个真子集且不可数,则B 不是闭集.但另一方面,对于{xn}⊂B 有{xn}S 收敛于x,则存在M ∈Z+使得当i >M 时xi= x,于是x ∈B,故B 是(X,TS)中的闭集,矛盾.从而证明了X 上的点列{xn}的T 收敛与S 收敛一定不一致.
2.3 实 例
用S 收敛来确定拓扑结构,即所谓的基本函数空间R(Rn).
对于n 维Euclid 空间Rn中的点x = (x1,x2,…,xn),记设p1,p2,…,pn为个非负整数,多重指标p 是指如下的有序n-数组p = (p1,p2,…,pn),记| p| = p1+ p2+ … + pn.对于每个多重指标p,引进偏微分算子,

设φ 为定义在Rn上的函数,称集合{x:φ(x)≠0}的闭包为φ 的支集,记为suppφ.
设φ 为定义有Rn上的函数,称Dpφ(如果存在)为φ 的p 阶偏导数.如果pj= 0,则表示不对xj求偏导数.如果所有的pj= 0(j = 1,2,…,n),表示不求任何偏导数.Rn上无限次可微复值函数的全体为C∞(Rn).C∞(Rn)中具有紧支集的函数的全体记为R(Rn).容易看出,C∞(Rn)、R(Rn)按照通常函数的线性运算都是复线性空间.
定义6 设{φm}⊂C∞(Rn)(m = 1,2,3,…),φ ∈C∞(Rn).如果对Rn中的任一紧子集K 以及任一多重指标p,{Dpφm}在K 上一致收敛于Dpφ,则称{φm}在C∞(Rn)中收敛于φ,记为
定义7 设{φm}⊂C∞(Rn)(m = 1,2,3,…),φ ∈R(Rn).如果满足:
①存在Rn的紧子集K,使得对这一切m = 1,2,3,…,有suppφm⊂K;
②对任一多重指标p,{Dpφm}在Rn上一致收敛于Dpφ.
则称{φm}在R(Rn)中收敛于φ,记为,{φm}而称R(Rn)按照所规定的线性运算及收敛概念为一基本函数空间.
易知,(R(Rn),TS)不仅是拓扑空间,而且是线性空间,以及其上的线性运算在拓扑TS下是连续的,因而其是拓扑线性空间.
[1]程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础[M].北京:高等教育出版社,1983.
[2]孙经先.非线性泛函分析序集一般原理的研究[J].徐州师范大学学报(自然科学版),2005,23(1):1-6.
[3]Crandall M G,Ishii H,Lions P L.Users guide to viscosity solutions of second-order partial differential equations[J].Bulletin of the American mathematical Society,1992,27(1):1-11.
[4]Lazer A C,Mckenna P J.On the existence of stable periodic solutions of differential equations of duffing type[J].American Mathematical Society,1990,110(1):125-133.
[5]Li D S,Liang Y T.Existence of periodic solutions for fully nonlinear first-order differential equations[J].Nonlinear Analysis,2003,52(4):1095-1109.

