基于最小体积约束的非负矩阵分解模型的高光谱解混算法探究
余肖玲,黄光鑫
(成都理工大学 管理科学学院,四川 成都 610059)
0 引 言
在测量光谱图像的过程中,受自然条件和环境等因素的影响,大多数地面的真实测量数据几乎不可能获得,从而导致图像中的端元无法自动获取.对于这种无法从图像中提取端元的情况,若能实现对高光谱遥感数据进行数据驱动下的盲分解,则非监督的混合像元分解就显得重要.非监督的混合像元分解,能做到的就是在完全不了解端元信息的情况下,直接以遥感图像本身为目标,根据混合像元的光谱模型及约束条件等信息,把混合像元分解为端元光谱矩阵及其在像元中所占的比例矩阵,即系数矩阵或丰度矩阵[1].在现有资料研究中,混合像元模型主要包括2 类:线性光谱混合模型和非线性光谱混合模型.近年来,随着对光谱混合特性的进一步研究,线性光谱混合模型越来越引起更多学者的重视[2-9].对此,本研究首先对线性光谱混合模型进行描述,然后在线性混合模型的基础上,再对混合像元分解算法进行讨论.
1 线性光谱混合模型
线性光谱混合模型[10]的表达式为,

式中,x 为m(m 为影像波段数)维混合像元光谱,是遥感影像图已获得的实际测量值,A 为m ×p(p 为端元数目)的端元矩阵,其中每一列代表一个端元的光谱向量,向量s 为像元中各端元的丰度,ε 为m 维模型误差或高斯随机噪声.
若把遥感图像中的全部像元均考虑在内,式(1)可写为,

式中,X ∈Rm×n,其列向量表示各个像元的光谱;S∈Rp×n构成系数矩阵或丰度矩阵.
在线性光谱混合模型中,系数矩阵S 需满足2个限制条件[6],即:1)非负性.
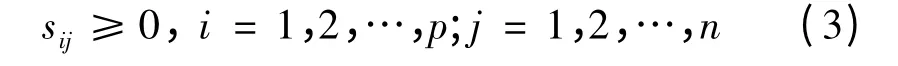
2)丰度和为1.

2 非负矩阵分解模型
约束非负矩阵分解(Constrained Nonnegative Matrix Factorization,CNMF)算法通过加入非负限制可将一个非负矩阵分解(Nonnegative Matrix Factorization,NMF)分为2 个非负矩阵A 和S 的乘积,
X = A × S
其中,A 为m × p 阶矩阵,S 为p × n 阶矩阵,p ∈min(m,n).
目标函数式为,

由式(5)可知,NMF 算法理论上就是一个最优化问题,其目的就是目标函数在基于欧氏距离的要求下寻找到最小值,并满足A 和S 满足非负性的约束[3].式(5)中,σ 和τ 是规则化参数,σ‖A‖2/2 和τ‖S‖2/2 为引入的平滑性约束,目的是调节逼近误差和平衡约束的消长关系.在寻求最小值的过程中,A 和S 遵循的迭代准则为,

在式(6)的指引下,式(5)是单调非增的.当A和S 值稳定时,目标函数值不再发生变化.在高光谱解混中,可以有意识地把X 设想成m 维混合像元光谱,利用上述迭代规则寻求满足非负性的端元矩阵和丰度矩阵.需要注意的是,为了满足式(4)的成立,每一步迭代后仍需对S 按,

做归一化处理[5].
3 基于最小体积约束的非负矩阵分解方法
基于最小体积约束的非负矩阵分解方法(Nonnegative Matrix Factorization Method Based on Minimum Volume Constraint,MVC-NMF)在最小二乘和凸面几何结合的基础上,把体积约束附加到NMF 中,其相应的目标函数式为,

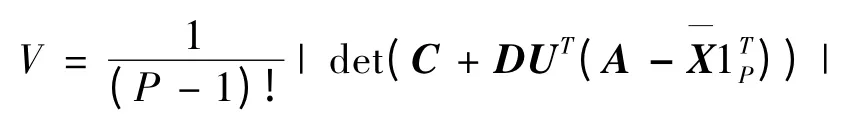
用来计算单体体积的惩罚项.φ ∈R.
把交替最小平方法引入到上述优化问题中,就可以利用,

把初始问题分解为2 个小问题.在计算过程中,保持矩阵A 和S 任何一个不变来交替更新另一个,并采用梯度投影学习规则强化每个小问题中的矩阵非负限制.若出现不满足约束限制的负值,则在保持非负变量不变的同时,利用函数max(0,x)将负值设定为0,则有,

将目标函数f(A,S)对矩阵S 求偏导数,
Sf(A,S)= AT(AS-X),
令,

则目标函数对矩阵A 的偏导数为,

由此,MVC-NMF 算法的具体步骤为:
①输入混合光谱数据矩阵X ∈Rm×n(m 为波段数,n 为像元数);
②用虚拟维度[9]的方法估计端元数P;
③从X 中任意选取P 列充当初始源矩阵A ∈Rm×P;
④生成初始系数矩阵S ∈RP×n,并根据式(7)对S 进行归一化处理;
⑤设定最大迭代次数MaxIter;
⑥根据式(10)分别更新A 和S 并根据式(7)对矩阵S 再做归一化处理;
⑦设置最大迭代次数MaxIter;
⑧若MaxIter 已达到最大值或目标值不再收敛,则算法结束;否则重复步骤⑥.
4 实 验
为了检验MVC-NMF 算法对混合像元分解的性能,在实验中,采用USGS 光谱库中的五条光谱来构建模拟数据,添加噪声所用的信噪比为30 dB,光谱曲线如图1 所示,同时,还将本算法与平滑LO 模约束的MVC-NMF(MVC-NMF with Smoothed LO norm Constraint,SC-MVC-NMF)算法的实验结果进行对比.
1)端元数不同时的实验对比.为了对比在不同端元数目情况下2 种算法的结果,实验中给模拟图像添加了30 dB 的高斯噪声且采用的最大迭代次数为60 次.MVC-NMF 算法和SC-MVC-NMF 算法均采用VCA+FCLS 进行初始化.将端元数设定为5、6、7时,2 种算法提取结果的运行时间及相似性测度的结果如表1 所示.
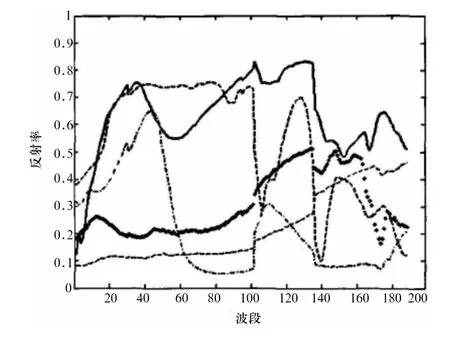
图1 构建模拟图像的5 条光谱
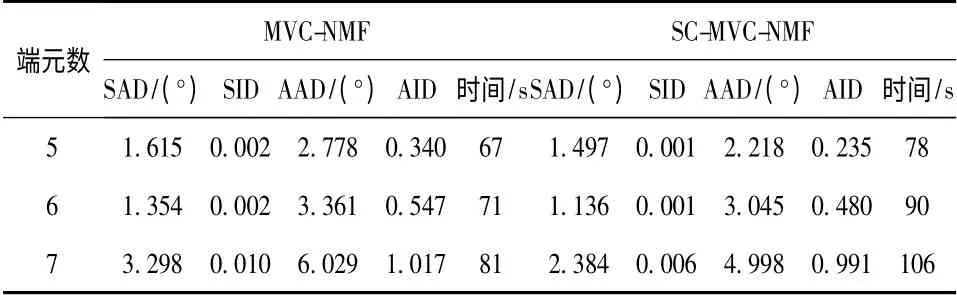
表1 端元数不同时的实验对比
由表1 可知,在端元数目不同的情况下,MVCNMF 算法的精度略低于SC-MVC-NMF 算法,但其运行时间明显较快.
2)噪声的稳健性对比.为了对比2 种算法的抗噪性,利用上述5 条光谱构建模拟图像,并在模拟数据中分别添加SNR =10、20、30、40 dB 的高斯噪声且设定最大迭代次数为60.MVC-NMF 算法和SCMVC-NMF 算法均利用VCA +FCLS 进行初始化.在不同的信噪比下,MVC-NMF 和SC-MVC-NMF 算法获取的端元光谱、丰度矩阵的相似性测度如表2 所示.

表2 噪声的稳健性对比
从表2 可以看出,在信噪比减小的情况下,2 种算法的结果都逐渐变差,尽管SC-MVC-NMF 算法运行时间略有增加,但其混合像元分解的结果始终优于本研究算法提取的结果.
3)实验结果表明,噪声的稳健性方面,在端元数不同的情况下,本研究算法收敛速度较快,但其混合像元解混的结果略差,因此,附加条件下MVCNMF 的改进成为下一步研究的重点.
5 结 论
本研究提出的MVC-NMF 算法对于高光谱图像混合像元分解问题有较大的实用价值,然而MVCNMF 算法在计算过程中表现出来的收敛效果略差的缺点,却影响了高光谱混合像元分解的效率,且很难找到最优解,这些劣势限制了非负矩阵分解模型的应用.因此,在以后的研究过程中,应进一步探索更为快速高效的高光谱混合像元分解的NMF 算法.
[1]贾森.非监督的高光谱图像解混技术研究[D].杭州:浙江大学,2006.
[2]Maurich D C.Minimum volume transforms for remotely sensed data[J].IEEE Transactions on Geoscience and Remote Sensing,1994,32(3):542-552.
[3]Lin C J.Projected gradient methods for non—negative matrix factorization[J].Neural Computaion,2007,19(10):2756-2779.
[4]Pauca U,Piper J,Plemmons R.Nonnegative matrix factorization for spectral data analysis[J].Linear Algebra and Application,2006,416(1):29-47.
[5]薛绮.基于线性混合模型的高光谱图像端元提取方法研究[D].长沙:国防科学技术大学,2004.
[6]Heinz D C,Chang C I.Fully constrained least squares linear spectral mixture analysis method for material quantification in Hyperspectral imagery[J].IEEE Geoscience and Remote Sensing Letters,2001,39(3):529-545.
[7]Miao L,Qi H.Endmember extraction from highly mixed data using mininlum volun ℃constrained nonnegative malrix factorization[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(3):765-777.
[8]Chang C I,Du Q.Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J].IEEE Transcation on Geoscience and Remote Sensing,2004,42(3):608-619.
[9]刘雪松.基于非负矩阵分解的高光谱遥感图像混合像元分解研究[D].上海:复旦大学,2011.
[10]赵春晖,成宝芝,杨伟超.利用约束非负矩阵分解的高光谱解混算法[J].哈尔滨工程大学学报,2012,32(3):96-99.
[11]施蓓琦,刘春,孙伟伟,等.应用稀疏非负矩阵分解聚类实现高光谱影像波段的优化选择[J].测绘学报,2013,46(3):351-358.

