龙格—库塔方法与差分法的比较
吴志强,张晏铭,秦浩东
(长春工业大学 基础科学学院,吉林 长春 130012)
0 引 言
对于一维常系数扩散方程,

把空间微分项用中心差商代替,就得到半离散的常微分方程组,

采用二阶龙格— 库塔方法对半离散的常微分方程组进行时间导数的离散,则有,

1 误差分析
对式(1),由于时间导数的离散采用二阶的龙格—库塔方法,这一格式的截断误差为O(τ2),式(2)的空间微分项用中心差分离散,故空间项的截断误差为O(h2),所以求解一维常系数扩散方程的龙格—库塔方法的截断误差为O(τ2+ h2).
2 稳定性分析
在进行数值模拟时,为保证计算稳定,必须选择合适的计算参数.在取定空间步长后,时间步长的选取必须满足一定的稳定性条件.为此,利用Fourier变换方法推导龙格—库塔方法的稳定性条件[1-7].
令,

则式(3)变为,
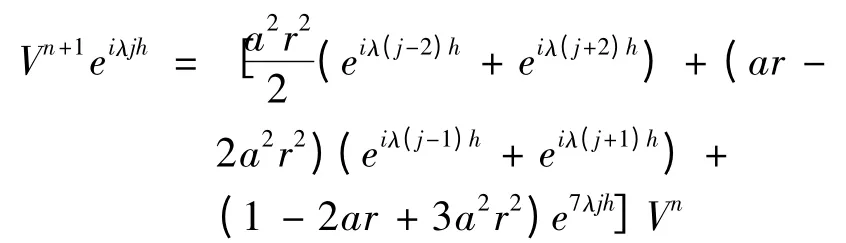
等式两边消去eiλjh,
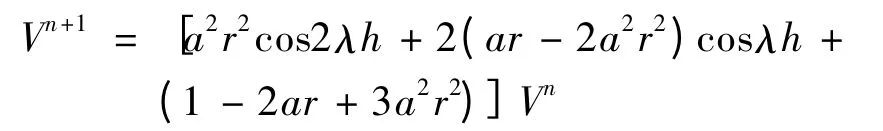
则增长因子为,

3 数值算例
对如下定解问题:
②u(x,0)= sinπx,当0 ≤x ≤1 时;
③u(0,t)= u(1,t)= 0,当t ≥0 时.
其解析解为,
u(x,t)= e-π2tsinπx.
对该算例用二阶龙格—库塔格式进行编程计算,并与显格式、隐格式和CN 格式方法进行比较.
当空间步长h = 0.1,网格比取r = 0.3,t = 0.5时,不同格式和解析解的对比图如图1 所示.

图1 不同格式计算的数值解和解析解的对比图(t = 0.5)
表1 为不同格式计算的数值解和解析解的对比.

表1 不同格式计算的数值解和解析解的对比
表2 为不同格式所用的计算时间.

表2 不同格式所用的计算时间
由表2 可以看出,龙格库塔方法是一种比较好的格式.隐格式和CN 格式在编程计算时要求解方程组,故计算量要比显格式大.但当网格比大于0.5时,显格式和二阶龙格库塔方法都发散.
当空间步长h = 0.1,网格比取时r = 0.55,t =1 时,不同格式计算的数值解和解析解的对比图如图2 所示.
当J = 10,dx = 0.1,dt = 0.001,r = 0.1,4 种方法的比较结果如表3.
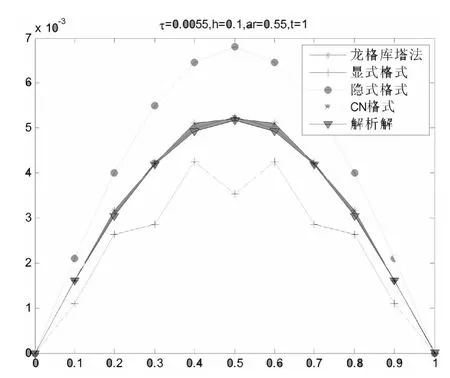
图2 不同格式计算的数值解和解析解的对比图(t = 1)

表3 4 种格式的迭代比较(J = 10)
当J = 20,dx = 0.05,dt = 0.0013,r = 0.5,比较结果如表4.

表4 4 种格式的迭代比较(J = 20)
由表3、4 可以看出,龙格—库塔方法在一定情况下,迭代次数较少,计算速度相对较快.
4 结 论
本研究主要分析了二阶龙格—库塔方法应用到求解扩散方程中的可行性:利用Fourier 变换得出其稳定区间;二阶龙格—库塔方法在一定情况下可提高精度,减少了求解扩散方程的计算量,求解方便;在一定精度条件下,龙格—库塔方法的迭代次数较少,计算速度快.
[1]李莎,王瑜.泰勒公式及其应用[J].科学之友,2012,33(11):136-137.
[2]王佩臣,袁海燕,刘鹏.有限差分法和隐式龙格—库塔法求解Burgers 方程[J].长春理工大学学报,2013,36(1-2):158-160.
[3]郭晓梅.常微分方程的数值解法[J].网络财富,2009,23(8):132.
[4]平根建.一阶线性微分方程的解法探析[J].沙洋师范高等专科学校学报,2012,13(2):72-73.
[5]李夏云,陈传淼.用龙格—库塔法求解非线性方程组[J].数学理论与应用,2008,28(2):62-65.
[6]李志毅,陈殿云,雷旭升.微分方程初值问题的GDQR 解法[J].数值计算与计算机应用,2005,26(2):135-140.
[7]薛毅.数值分析与实验[M].北京:北京工业大学出版社,2006.
[8]数值方法中Runge-Kutta 方法改进的探讨[J].衡水学院学报,2014,16(4):23-26.

