近水面双圆柱壳耦合声散射研究

张林根，吴文伟，张涛，吴有生

近水面双圆柱壳耦合声散射研究

张林根1，吴文伟2，3，张涛2，3，吴有生2，3

（1海军装备部，北京100081；2中国船舶科学研究中心；3船舶振动噪声重点实验室，江苏无锡214082）

文章针对小水线面双体船水下片体结构的声辐射特征，建立了近水面双柱壳的耦合声散射模型，通过对双片体结构与水面间耦合散射声场的数值计算，分析了双片体结构参数和水面镜面效应对散射声场的影响规律，提出了相应的噪声控制建议。

双体船；声散射；远场辐射声；镜面效应

1 引言

小水线面双体船是一种靠水下双柱型片体提供浮力，并在水线处片体水线面宽度最小化的船型，具有非常好的耐波性和兴波阻力性能。因此，从结构形式上看，小水线面双体船的片体结构是由圆柱壳形式的下潜体和双层板架的支撑结构组成（图1）。

船上机械设备激励船体结构产生的结构噪声可通过船体结构传递到水下片体结构，并与流体介质耦合，引起水中辐射噪声[1]。因此，为了降低和控制这部分机械系统引起的水下辐射噪声，通常在设计中会将对水下噪声有贡献的辅机设备布置在水线面以上的甲板上，水下片体结构中仅布置推进系统，尽可能减少结构噪声传递到水下片体结构。水下片体结构作为重要的水下噪声辐射体，其受激与声辐射特性对双体船水下辐射噪声的影响至关重要，该性能的改进优化是声学设计的重要内容，为此，首先要建立该片体结构水下声辐射计算模型。小水线面双体船的水下片体结构潜深较浅，在计算该结构受激引起的水下噪声时，需要考虑双体船两片体之间以及水面作为压力释放边界的声散射作用，这对于从机理上掌握双体船水下噪声场的声学物理图像具有重要意义。

早些年，国内外一些研究者针对多圆柱结构的声散射问题已开展过一些研究。如上世纪七十年代，Young等人[2]开展了并排双圆柱壳的声散射研究，Sherer等人[3]开展了多圆柱壳的耦合声散射研究。不过在这些研究中均只考虑了圆柱壳的刚性散射而忽略了辐射声。白振国等人[4]针对无限水域的三圆柱壳声辐射问题也开展了圆柱壳间声散射的研究。为了建立小水线面双体船片体结构水下声辐射计算模型，本文针对片体典型的水下近水面双圆柱壳结构，首先采用虚源方法模拟水面的声学边界条件，将双体船近水面下潜体的声散射作用转化为全空间的四圆柱声散射问题，再利用Graff加法定理求解刚性散射和辐射耦合方程，并获得远场声压的分布，从而得以分析圆柱壳之间以及水面影响的耦合声散射效应及规律。最后，文中通过典型算例分析了水面以及结构障碍物散射作用对水下声场的指向性影响。

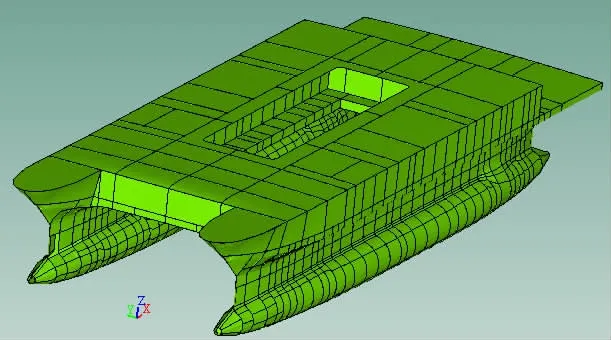
图1 双体船Fig.1 SWATH

2 双体船耦合声场特征分析

2.1 近水面双圆柱壳结构声散射模型

针对双体船片体典型结构声辐射问题，建立无限长双体圆柱壳简化模型，并采用虚源方法使水面的声学边界条件自动满足，使半无限空间两圆柱的声散射问题转化为全空间四圆柱声散射问题。图2为考虑了水面影响的双圆柱壳结构声散射物理模型示意图。四个半径分别为a1、a2、a3、a4的无限长均匀弹性圆柱壳平行排列，圆柱1与3关于水面对称，声压反向，圆柱2与4关于水面对称，声压反向。在每一圆柱的圆心处分别定义局部极坐标系（ri，φi），则j号圆柱壳的圆心在定义于i号圆柱壳圆心处坐标系中的坐标为（Lij，φij）。根据此定

假定壳体浸没在无限的可压缩理想流体介质中，流体中的声速为c。当某一圆柱如圆柱1，受外部机械激励将在水下形成稳定的噪声场。由于圆柱2以及水面的声散射效应，整个声场由圆柱壳1受机械激励产生的直达声以及该直达声作为入射声波引起弹性圆柱壳与水面散射形成的混响声组成。假定仅在圆柱壳1上有机械激励力作用，当有其他外部激励同时作用时，可利用叠加原理求解。

对于观察点o，总声场p由直发声与混响场构成，混响场包括刚性散射场与辐射场：

图2 近水面双圆柱壳声散射模型Fig.2 Physical model of near surface twin cylinders

式中：p0为直发声，为作用在圆柱1上的外力在无限自由空间产生的声压（i=1，2，3，4）为圆柱壳i的刚性散射声；（i=1，2，3，4）为圆柱壳i的辐射声。

根据圆柱壳在流固交界面上所需满足的连续性条件：

式中：ρ0为流体密度；ω=2π f为圆频率，f为激励频率；wj为圆柱壳j表面振动位移。对于圆柱壳j而言，其入射声场可视为所有圆柱壳i i≠（）j引起的刚性散射及辐射声场的叠加：

根据刚性散射的定义，在圆柱壳j表面满足：

由（1）式、（2）式和（3）式，得到：

2.2 圆柱壳振动方程

圆柱1受机械激励将产生直达声p0，这可通过单圆柱的流固耦合声辐射理论直接求解。本文主要解决混响声的计算方法。考虑弹性薄壳，壳体受外部激励产生的振动可用Donnel方程描述。对于圆柱壳1：

式中：v1、w1分别表示圆柱壳1的周向和径向位移为壳体展开为平板时的纵波波数，E，ρs，μ分别为材料的杨氏模量、密度和泊松比；h1为圆柱壳1厚度；；二维圆柱的壳体振动位移与轴向位置无关，其形式解为：

将（7）、（8）式代入（5）、（6）式，得到

同样，可给出圆柱壳2、3、4的振动方程，整理后写成矩阵形式：

柱壳j表面的n阶周向模态分量。到目前为止，这些系数均为未知量。在下一节，将给出这些系数的求解方法，并进一步可根据（11）式计算圆柱壳的位移模态分量以及辐射声压。

当圆柱壳1上有机械激励F1作用时，产生的直达声p0可表示为：

式中：

在本文考虑的线弹性范围内，根据理想流体的假定，声压psj、prj满足Helmholtz方程，利用无穷远处的声压辐射条件，圆柱壳j引起的刚性散射声压和辐射声压可在自身的局部坐标系下表示为：

式中：

形式时显然满足水面声压为0的条件。

圆柱壳j对自身产生的周向模态分量可表示为：

将（13）式代入（4）式得到：

各圆柱壳除受自身辐射声的作用，也受其它圆柱壳辐射声的作用。为确定圆柱壳之间通过辐射声场的相互作用大小，需要利用Graf加法定理[5]将圆柱壳i的辐射声场在另一圆柱壳j所在的坐标系中表示。根据该定理，Hankel函数可表示为：

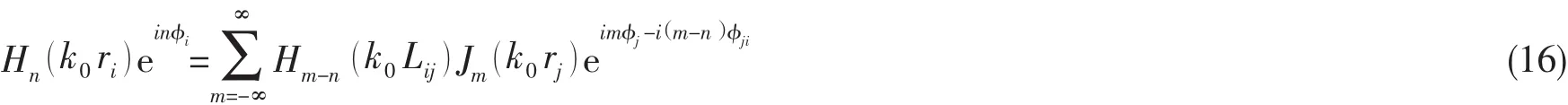
ij

将（16）式代入（13a）式：

因此，圆柱壳i产生的辐射声压作用在圆柱壳j上的模态分量为：

由上式可以看出，圆柱壳i产生的辐射声压作用在圆柱壳j上时，每一个周向模态上都是圆柱壳i所有周向模态叠加的结果。

多体问题的复杂性表现在，各圆柱壳之间不仅通过辐射声场发生相互作用，而且由于各圆柱壳的存在，将对入射声波产生散射。圆柱壳1、2、3之间通过刚性散射声场的相互作用可用与上式相近的形式表示）等系数为未知量,可利用各圆柱壳表面的刚性散射边界条件求解。

同理，直达声作用在圆柱壳j上的模态分量为：

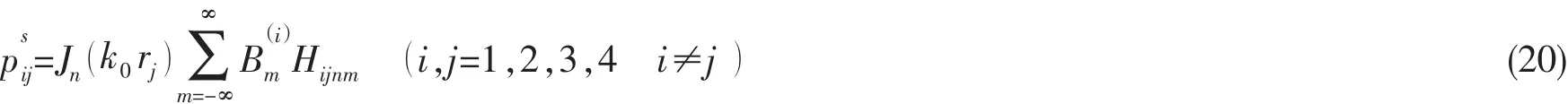
将（17）、（19）式和（20）式代入（3）式可得到一组关于的方程组。

将（20）式中的n依次从-N取到N，并将关于m的无穷级数求和在m=N处截断，则上式构成了4×（2N+1）个线性方程。系数）与模态位移）的关系可用矩阵联系起来。经过以上的分析过程，由（13）、（18）式和（19）式可知，（9）式中关于声压的未知量均以模态位移的函数表示出来。同样，将（9）式中的n依次从-N取到N，构成4×（2N+1）个线性方程，）可直接求解。进一步可求出系数以及整个声场的声压分布。

3 数值计算与结果分析

以某小水面双体船为例，该船船体结构参数为：a1=a3=2 m，a2=a4=2 m，L12=10 m，L13=12 m，h1=h3= 0.008 m，h2=h4=0.008 m。分别计算了在圆柱壳1上，0°方位作用法向单位激励力时，从20 Hz到1 000 Hz的远场声压分布。计算针对自由声场中的单个圆柱壳，自由声场中的双圆柱壳和近水面的双圆柱壳三种工况（本计算选取的截断数N=10）。

图3－6给出了20 Hz、100 Hz、500 Hz和1 000 Hz时，在180°-360°之间不同观察角度的声压。可看出，旁边圆柱壳对360°附近方位的声传播有明显的遮蔽效应，对180°附近方位的声波有一定的增强作用。随频率升高，旁边圆柱壳的遮挡效应增强，但遮挡的区域有所减小。而水面作为压力释放面，对近水面观察点的声压有较为明显的降低，这种影响效果随频率升高而降低。此外，水面作为散射边界，进一步改变了声场的指向性，这表现为在声压的指向性图上出现了较多的极大值。在水面和双圆柱壳形成的耦合声场中，正对障碍物的声传播受到明显的遮挡，最大声压点的幅值与方位均发生改变。当初始的最大声压出现在水平方位时，由于水面的影响，低频最大声压将有明显的降低。

图3 不同观察角度的远场声压（20 Hz）Fig.3 Sound pressure of different observation angle(20 Hz)

图4 不同观察角度的远场声压（100 Hz）Fig.4 Sound pressure of different observation angle(100 Hz)

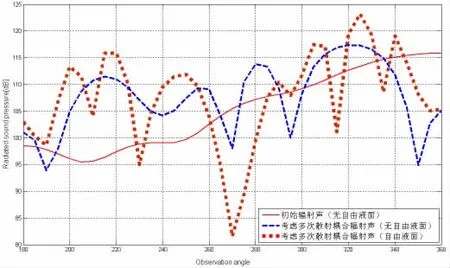
图5 不同观察角度的远场声压（500 Hz）Fig.5 Sound pressure of different observation angle(500 Hz)

图6 不同观察角度的远场声压（1 000 Hz）Fig.6 Sound pressure of different observation angle(1 000 Hz)

图7 远场声压的频谱特征（180°）Fig.7 Far field sound pressure(180°)

图8 远场声压的频谱特征（225°）Fig.8 Far field sound pressure(225°)

图9 远场声压的频谱特征（270°）Fig.9 Far field sound pressure(270°)

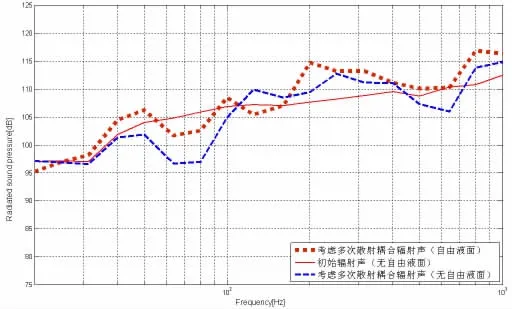
图10 远场声压的频谱特征（300°）Fig.10 Far field sound pressure(300°)

图11 远场声压的频谱特征（330°）Fig.11 Far field sound pressure(330°)

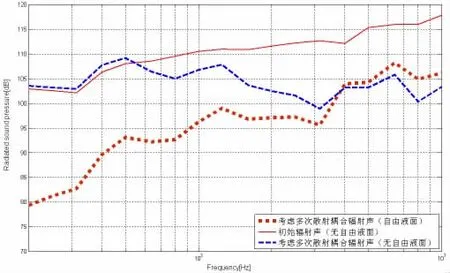
图12 远场声压的频谱特征（360°）Fig.12 Far field sound pressure(360°)

图7-12分别给出了180°、225°、270°、300°、330°和360°观察方位上，20-1 000 Hz频段范围的远场声压频谱特征。可看出旁边圆柱壳对360°附近方位的声波传播有明显的阻碍作用，且随频率升高增加，1 000 Hz达到15 dB的遮挡效果。由于声散射的作用，对其余角度有一定增强的效果。水面的压力释放效应对近水面观察点的声压在低频有显著降低，随频率升高到约200 Hz影响减弱，甚至有增强的效果。远离水面的观察点声压在绝大部分频率均有一定的增强。

5 结论

为探索双体船结构声辐射的机理和物理图像，利用虚源方法建立近水面双圆柱壳的耦合散射模型，分析研究了双体船水下双圆柱潜体之间以及水面反射耦合效应的基本规律。通过具体算例的分析和计算，可以得出以下主要结论：

（1）结构障碍物和水面边界对水下辐射声场的指向性有较大影响，最大声压幅值与指向角均发生了变化。考虑耦合效应后，辐射声压在周向的分布更加复杂，出现了更多蝶瓣。在潜体结构表面敷设吸声材料，将有效地抑制散射声。

（2）水面的压力释放效应显著降低了近水面的远场声压，而对于远离水面处的声压在绝大多数频率上有所增强。自由液面效应的影响随频率升高而减小。如果初始声压的最大值出现在水平方向，水面的存在将使低频辐射声显著降低。这说明潜体内机械设备的支撑位置优先选择在圆柱壳水平中线的两侧将更加有利于降低船体的结构噪声。

[1]Kim Jae-Ho.Prediction of underwater radiated noise by machinery vibration for SWATH vessels[J].Inter-noise,2003.

[2]Young J W.Multiple scattering by two cylinders[J].J Acoust.Soc.Am.,1975,58(6):1190-1195.

[3]Sherer S E.Scattering of sound from axisymetric sources by multiple circular cylinders[J].J Acoust.Soc.Am.,2004,115 (2):488-496.

[4]白振国.三圆柱壳多体结构的声遮蔽特征计算方法研究[R].无锡:中国船舶科学研究中心科技报告,2012.

[5]Abramowitz M.Handbook of mathematical functions[M].1964.

Study on sound scattering by underwater twin-cylinder near the surface

ZHANG Lin-gen1,WU Wen-wei2,3,ZHANG Tao2,3,WU You-sheng2,3
(1 Naval Equipment Department,Beijing 100081,China;2 China Ship Scientific Research Center; 3 Ship Vibration and Noise Key Lab of China,Wuxi 214081,China)

In order to study the radiated sound characters of SWATH(small waterplane-area twin-hull ship), the coupled scattering model of underwater twin-cylinder structure near the surface is developed,and the far field sound pressure excited by external force from machinery is solved by using numerical method.As an example,the effect of sound scattering by structure and free surface of a typical SWATH is analyzed,and the main conclusions and control methods are also presented.

twin-cylinder;sound scattering;far field sound pressure;mirror effect

O427.2

A

10.3969/j.issn.1007-7294.2014.07.017

1007-7294（2014）07-0864-07

2014-05-10

张林根（1965-），男，博士，高级工程师；

吴文伟（1962-），男，中国船舶科学研究中心研究员，E-mail：Wuww@cssrc.com.cn。