近距空爆载荷作用下叠层薄板抗爆机理数值分析
刘燕红,陈长海,朱锡,李万,侯海量,唐廷
近距空爆载荷作用下叠层薄板抗爆机理数值分析
刘燕红a,陈长海b,朱锡b,李万c,侯海量b,唐廷b
(海军工程大学a.动力工程学院;b.舰船工程系;c.兵器工程系,武汉430033)
为探讨战斗部近距爆炸下大尺寸叠层薄板的抗爆机理,结合模型试验,采用有限元对近距空爆载荷作用下固支叠层方板的爆炸载荷、变形过程、应变分布和变形吸能情况进行了数值分析,并与相同材料同等总厚度的单层方板进行了比较。在此基础上,进一步分析了层间间距、叠层层数和边界条件对叠层板抗爆性能的影响。结果表明,较单层板而言,试验工况下叠层板的变形吸能较大,但其最大应变较小且应变分布更为均匀;而在极限应变状态下,叠层板变形吸能较单层板有很大提高;适当增大层间间距能一定程度地提高叠层板的抗爆变形能力,但过大的层间间距不利于叠层板的整体协调变形;层数的增加能提高叠层板的抗爆变形能力;简支边界条件较固支边界条件而言,能更充分地发挥叠层板的抗爆变形吸能能力。
爆炸力学;近距空爆载荷;叠层薄板;抗爆机理;数值分析
1 引言
爆炸载荷作用下金属结构主要通过塑性大变形来吸收冲击波能量。而对于金属平板结构而言,爆炸载荷作用下冲击波能量大部分通过结构的弯曲和薄膜拉伸这两种塑性大变形的方式耗散掉[1-2]。而爆炸载荷作用下薄板在产生大变形的情形下,薄膜拉伸效应较为明显,此时弯曲应变效应往往可以忽略[2-4]。文献[2-4]对金属薄板结构的薄膜效应进行了理论分析,并指出爆炸载荷下薄板应尽可能设计成工作在薄膜应力状态下,这样可以更有效地发挥其抗爆吸能能力。基于这一思想,本文提出多层薄板结构即叠层板结构,并试图通过数值仿真分析其抗爆机理。目前,关于爆炸载荷下金属薄板的动态响应及其失效模式的研究较多,包括圆板[5-6]、方板[7-9]和矩形薄板[10]等。最近,研究者们对爆炸载荷下加筋板的动态响应问题开展了大量的试验[11-12]和数值仿真[13]研究。然而,这些研究大多集中于单层平板或板架,对于多层薄板结构的抗爆问题研究较少。文献[14]开展了双层间隔钢板的抗爆试验,然其主要目的是与双层泡沫夹芯结构进行对比,未见有双层无间隔钢板的分析。此外,近年来出现了大量关于双层平板夹芯结构抗爆响应问题的研究,如文献[15-17],但均与本文所提出的叠层板结构的抗爆响应问题存在较大差异。
随着反舰武器的发展,掠海飞行的半穿甲导弹已成为现代水面舰船面临的主要威胁,其作用方式通常是穿透舷侧外板后在舰船内部舱壁附近爆炸。因此,如何使内部舱壁结构在近距空爆载荷作用下尽可能多地吸收爆炸冲击波能量,以最大限度地减小冲击波对邻近舱室的毁伤程度和毁伤范围,成为舰船抗爆防护结构设计的重点。而本文提出的叠层板结构应该能够满足舰船抗爆防护结构设计中的抗爆吸能要求,但是目前对于其在近距空爆载荷作用下抗爆机理问题的研究还未见报道。
本文拟采用有限元数值仿真,结合模型试验,对近距空爆载荷作用下固支大尺寸叠层薄板结构的抗爆机理进行分析,并与相同材料同等总厚度的单层板进行比较。通过比较得到叠层板结构相对于单层板抗爆性能优劣的情况,并进一步分析叠层板抗爆性能的影响因素。
2 试验设计与实施
试验模型为一叠层板,该叠层板由4块1 mm厚的Q235低碳钢板叠层放置而成,4块薄钢板的总体尺寸均为700 mm×700 mm。试验中边界条件很重要,为此专门设计了一个方形钢质支座结构作为试验固定装置,支座的框架夹具面板厚度为20 mm。试验时将钢板夹于框架面板和底部支座之间,四周通过24个螺栓固定,以保证模型边界不会出现较大的面内移动。由于框架夹具面板四周有一定宽度,因而模型的实际抗爆面积为500 mm×500 mm,整个支座的高度为200 mm。试验时,将TNT炸药置于模型中心的正上方,并用绳子将炸药的位置固定(见图1)。试验条件为:装药量为400 g,装药形式为柱状,装药尺寸131.2 mm×50.2 mm,爆距为148 mm。为了比较,对单块4 mm厚的Q235钢板也进行了试验,其尺寸与叠层板相同,试验条件也与叠层板完全一致。为便于分析,称单层板试验为工况1,叠层板试验为工况2。
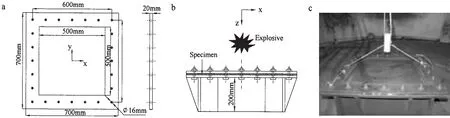
图1 试验装置示意图和照片Fig.1 Sketch and photograph of the experimental setup
3 有限元计算模型

式中:σd为动态屈服强度;σ0为静态屈服强度;Eh为应变硬化模量;εp为有效塑性应变;ε˙为等效塑性应变率;D、n为常数,对于低碳钢,通常取D=40.4/s,n=5。材料失效模型采用最大等效塑性应变失效准则。钢板的材料参数通过准静态试验获得,具体参数为:密度ρ=7.8 g/cm3,弹性模量E=210GPa,泊松比ν=0.3,准静态屈服强度σ0=235 MPa,应变硬化模量Eh=250 MPa。考虑到近距空爆载荷作用下结构的应变率效应较大,且中心点处易产生拉伸失效,因此仿真计算中材料的失效应变取为εf=0.411[18]。
炸药和空气均采用DMAT欧拉单元。炸药的爆轰过程通过JWL状态方程描述:

采用动态非线性有限元分析程序MSC/Dytran模拟结构的动态响应。仿真计算中,叠层板各层以及单块板均采用四边形壳单元进行模拟,边界条件均为四边固支。叠层板各层之间的间距为0.05 mm,各层之间定义了自适应接触,以避免单元畸变,同时也是为了模拟实际抗爆过程中各层之间的接触碰撞过程。
钢板材料采用双线性弹塑性本构模型,材料的应变率效应由Cowper-Symonds(C-S)模型描述:
式中:p为压力,A、B、R1、R2和ω为常数,η=ρ/ρ0,ρ0为初始密度;e为炸药的质量比内能。仿真计算中TNT炸药的各材料参数为:A=52.42 GPa,B=0.768 GPa,R1=4.2,R2=1.1,ω=0.34,e=4.19 kJ/g,初始密度ρ0=1.54 g/cm3。假设空气为无粘性理想气体,冲击波在空气中的传播用理想气体状态方程模拟,即:

式中:γ为绝热指数,e为空气的质量比内能。空气介质的状态参数为:初始密度ρ0=1.29 kg/cm3,初始压力p0=101 kPa,绝热指数γ=1.4,初始比内能e=0.197 kJ/g。空气边界为可流入流出边界。欧拉单元与拉格朗日单元之间的耦合采用一般耦合方式,通过建造虚拟单元来形成封闭耦合面,仿真计算模型如图2所示。
4 仿真计算与试验结果比较分析
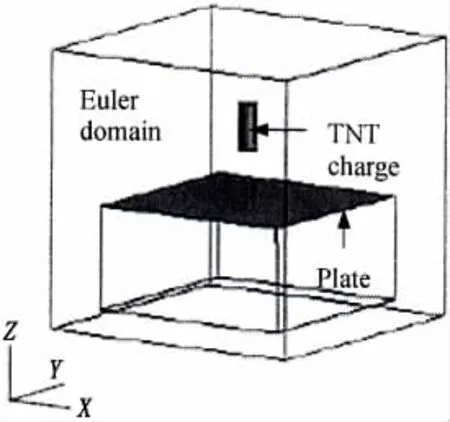
图2 仿真计算模型示意图Fig.2 Schematic of the model for numerical simulation
工况1试验后单层板的变形如图3a所示。由图可看出,在板的中部出现了明显的“烧灼”现象,“烧灼直径”约为100 mm,这种现象是由于炸药对板材的爆轰褪色作用引起的[6-10]。在“烧灼”区域的外围出现了较大的碟形变形区,变形大体上是对称的,而在板的对角线处出现了不明显的塑性铰线。通过测量得到板中心的最大挠度为42.3 mm。仿真计算得到的单层板最终变形如图3b所示。计算结果显示,t=1.0 ms时刻后,板的变形趋于稳定,存在小量的弹性振动。从图3b可看出,板中心部位出现了一个圆形变形区,直径约为120 mm,这比试验得到的“烧灼”区的直径稍大。仿真计算得到的单层板中心点处最大位移时程曲线如图4所示,从图中可以看到单层板响应后期的弹性振动现象。通过对1.0 ms时刻以后板中心点处的最大位移取平均值,得到单层板中心的最大挠度约为42.1 mm,较试验值稍小。

图3 工况1单层板的变形比较Fig.3 Comparison of deformation for single-layer plate in case 1
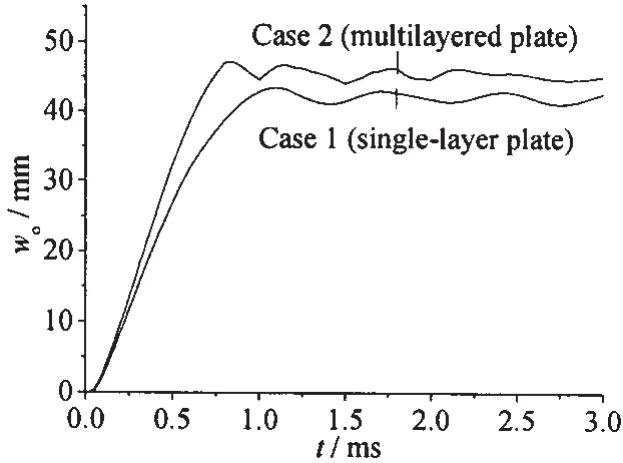
图4 板中心点处最大位移时程曲线Fig.4 History of maximum displacement at centre points of the plates

图5 工况2叠层板的变形比较Fig.5 Comparison of deformation for multilayered plate in case 2
图5a为工况2试验后叠层板的整体变形图。从图中可看出,板对角线处出现了明显的塑性铰线。此工况中也存在烧灼现象。“烧灼直径”约为102 mm,与工况1中的“烧灼直径”值接近。这是由于工况1和工况2两种工况之间试验条件相同所致。叠层板“烧灼”区以外也出现了碟形变形区,不过该碟形变形区的面积较单层板要大得多。通过测量得到叠层板中心点处最大位移为47.3 mm。图5b为t=0.8 ms时刻仿真计算得到的叠层板变形图,该时刻以后整个叠层板的变形趋于稳定,并存在一定程度的弹性振动。由于各层之间的位移变化基本一致,因此图4中叠层板的位移取的是四层板中心点处位移w0的平均值。比较图3b和图5b可看出,相比单层板而言,叠层板边界出现了明显的塑性变形,中部碟形变形区的大小较单层板要大得多,这与试验结果是一致的。此外,叠层板的变形稳定时间较单层板要早。这是由于叠层板总体的刚度较单层板要小,在抗爆过程中的横向变形速度较大所致。叠层板中心点处最大位移随时间的变化情况如图4所示。通过对0.8 ms时刻以后叠层板中心点处的最大位移取平均值,得到叠层板的最大挠度为45.1 mm,较试验值要小。这主要是由于试验过程中叠层板边界出现了一定程度的褶皱现象(图5c),使得叠层板产生了一定的面内位移,从而导致试验结果偏大。通过与试验结果的比较可知,仿真计算结果与试验结果吻合较好,验证了数值仿真算法的合理性和可靠性。
5 试验工况下叠层板抗爆机理对比分析
5.1 爆炸载荷分析
炸药近距爆炸下,结构承受的载荷为强动载荷,局部效应较为明显,且在冲击波载荷作用初期,存在爆炸流场与结构的流固耦合效应[19]。由于此耦合效应的存在,使得叠层板迎爆面反射冲击波压力的作用过程与单层板(以下均指材料和总厚度均与叠层板一致的单层板)出现较大差别。图6给出了本文试验条件下,仿真计算得到的工况1单层板和工况2叠层板中心点处反射冲击波压力时程曲线。从图中可看出,在冲击波作用初期,叠层板的反射冲击波压力峰值较单层板要小。这是由于在冲击波载荷作用初期,叠层板只有第一层直接承受冲击波载荷,而单层板则是整块板,因而根据流固耦合作用原理可知[20],质量较轻的叠层结构加速度较大,其在冲击波作用过程中能够有效减小结构表面的反射冲击波压力峰值。而从另一方面来理解,则是由于单层板直接承受载荷的惯性质量较大且刚度较大,使得其反射冲击波的峰值压力较叠层板结构要大,这与加筋板局部爆炸冲击载荷研究的结论是一致的[21]。
从图6中可进一步看出,在冲击波作用后期即反射冲击峰值压力过后,单层板表面反射冲击波压力迅速衰减,而叠层板结构表面反射冲击波压力的衰减速度较单层板要慢。这主要是由于局部冲击载荷下结构的表面效应引起的[22],即连续的结构表面的形状变化以及结构的持续运动使得反射冲击波压力发生改变,进而使得反射冲击波的持续时间也发生变化。叠层板结构由于弯曲刚度较小,中点处的运动速度大,形状改变得较快,因而冲击波持续作用的时间较单层板要长,反射冲击波的衰减速度较单层板要慢。
5.2 变形过程分析
近距空爆载荷下,固支大尺寸方板的变形过程与小尺寸方板存在较大差异。对于大尺寸方板而言,边界的变形较小,局部效应更为明显[23]。图7为工况1爆炸载荷下单层板动态变形过程的等高线。由图可知,单层板的变形首先从中部产生,然后向边界扩展。当t=0.4 ms左右,变形扩展至边界。当t= 1.0 ms左右变形趋于稳定,形成类似于“四坡顶形”的变形机构,对角线处形成不太明显的塑性铰线。计算结果显示,相对于板的中部而言,单层板边界附近的变形位移值很小,变形集中于板的中部。
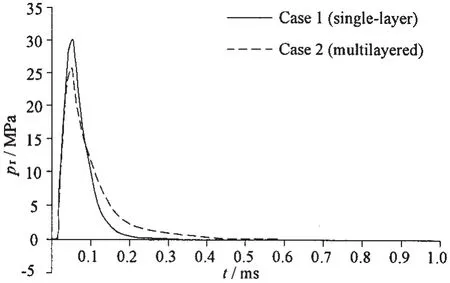
图6 中心点处反射冲击波压力时程Fig.6 History of reflected shock wave pressure at centre point

图7 单层板的变形等高线Fig.7 Deformation contour line of single-layer plate
与单层板不同的是,叠层板的变形过程要更为迅速,这主要是由于叠层板的刚度较小所致。图8给出了叠层板第一层的动态变形过程的等高线。当t=0.2 ms左右,叠层板的变形就已扩展至边界。随后,由于叠层板各层之间存在短暂的碰撞和动量传递过程,叠层板各层的变形迅速均匀化,并在对角线处出现塑性铰线。当t=0.8 ms左右,叠层板的变形趋于稳定,并在对角线处形成较明显的塑性铰线。计算结果显示,叠层板边界附近的变形位移值较单层板边界附近要大。进一步比较图8和图7可知,尽管叠层板的变形模式与单层板相似,但其变形速度及其最终变形程度均较单层板要大。

图8 叠层板(第一层)的变形等高线Fig.8 Deformation contour line of multilayered plate(the first layer)
5.3 应变分布分析
为了对比分析叠层板和单层板变形机理的差异,对单层板和叠层板中薄膜拉伸应变和弯曲应变的分布及其程度进行分析。如图9所示,取板的1/4对称平面,沿坐标x轴方向和对角方向分别选取两组单元,每组包含11个单元,自坐标原点(即板的中心点)处的单元往边界依次编号。组1(即Group 1)的单元沿板中线x轴方向,组2(即Group 2)的单元沿板的一条对角方向。仿真计算过程中,分别提取所选取单元的应变值进行分析。需要指出的是,叠层板结构取的是第四层板上的单元。薄膜拉伸应变水平可由仿真计算得到的单元中面应变εmid表示,而弯曲应变的程度则可通过计算单元上下表面应变的差值得到,即εd=εlower-εupper,其中εd表示单元弯曲应变的程度,εlower表示单元下表面的应变,εupper表示单元上表面的应变。
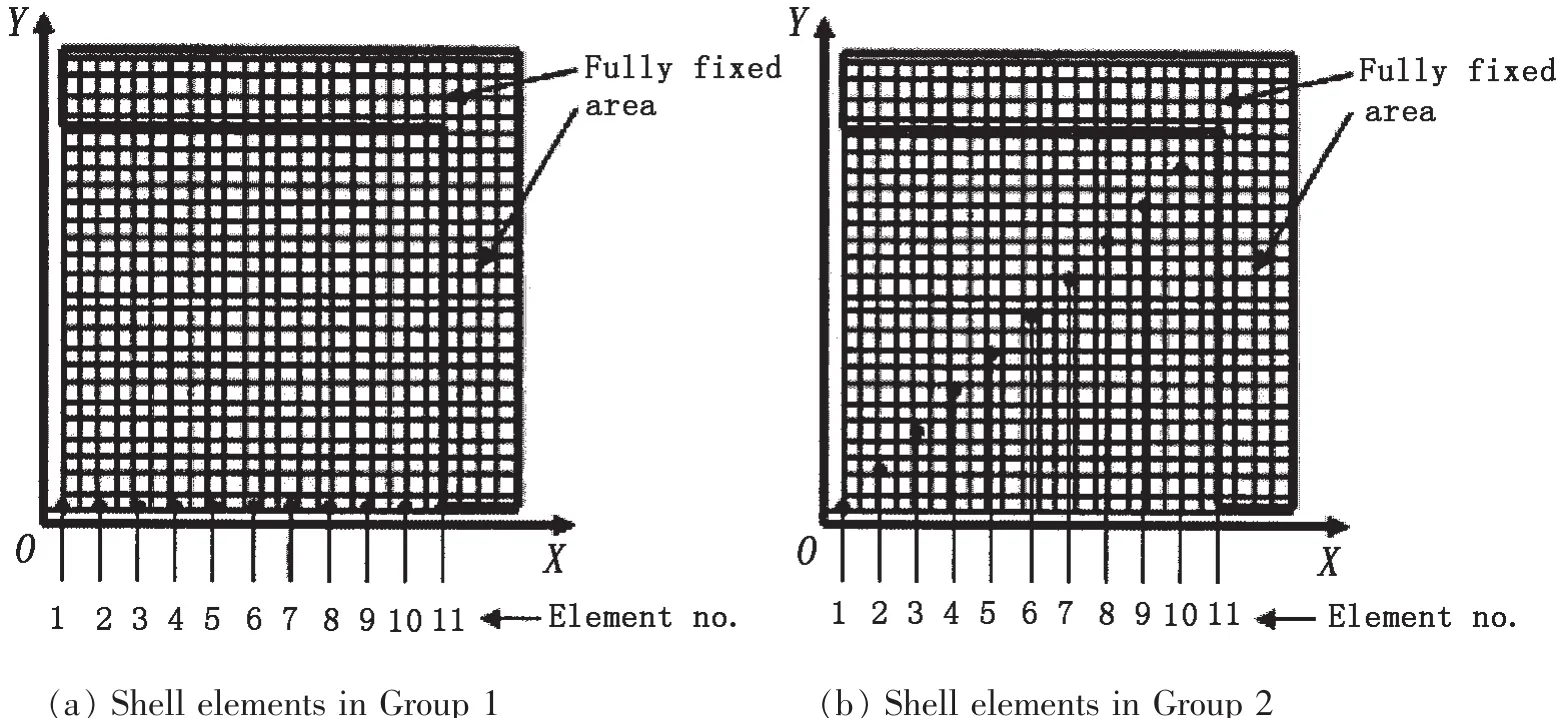
图9 两组所选取单元的位置Fig.9 Locations of the selected elements in the two groups
单层板沿x轴方向(即组1)各单元的应变发展及最终的应变分布如图10所示。由图10a和b可看出,εmidx和εmidy均随时间增长而增大,且应变自边界沿板的中心扩展。当t=1.0 ms左右,中心点处的中面应变εmidx和εmidy达到最大,均为2.2%。而在边界附近,单元的应变很小。由此可见,对于单层板而言,最大的薄膜拉伸应变发生在板的中心,边界附近的拉伸应变几乎为0,即边界附近几乎没有发生拉伸变形。

图10 单层板沿x轴方向(组1)单元应变分布Fig.10 Strain distribution of the shell elements along the x axis(Group 1)in single-layer plate
图10c和d为单层板沿x轴方向各单元的弯曲应变水平的分布情况。由图10c可看出,弯曲应变随时间的增长而增大。边界附近的弯曲应变很小,而在中心部位,弯曲应变最大。结合图10d可进一步看出,弯曲应变像波浪一样,从固支边界向中心部位传播。当t=1.0 ms左右,板的变形趋于稳定,最大的弯曲应变发生在板的中心部位,而边界附近的弯曲应变很小甚至出现负值。

图11 单层板沿对角方向(组2)单元应变分布Fig.11 Strain distribution of the shell elements along a diagonal(Group 2)in single-layer plate
图11给出了单层板沿对角方向各单元的应变发展及最终分布情况。由于对称性,只给出了εmidx和εdx的分布情况。由图11a可看出,单层板沿对角方向单元的薄膜拉伸应变分布情形与沿x轴方向相似。而从图11b则可看出,与沿x轴方向类似,单层板对角线方向εdx也呈现出波浪形的传播现象,且稳定状态下,最大弯曲应变也发生在板的中心部位,边界附近的弯曲应变很小甚至出现负值。

图13 叠层板沿对角方向(组2)单元应变分布Fig.13 Strain distribution of the shell elements along a diagonal(Group 2)in multilayered plate
叠层板沿x轴方向(即组1)各单元的应变发展及最终的应变分布如图12所示。通过比较图12a-b与图10a-b可知,尽管叠层板沿x轴方向单元的εmidx和εmidy的最大值也均发生在中心部位,但叠层板εmidx和εmidy的分布较单层板要更为均匀;虽然叠层板边界附近的薄膜拉伸应变较单层板要大,但其中心部位的最大薄膜拉伸应变却较单层板要小,即中心部位的εmidx和εmidy分别为1.6%和1.7%。
进一步比较图12c-d与图10c-d可得,叠层板沿x轴方向弯曲应变的分布形状与单层板相似,呈现波浪式的形状,最大弯曲应变也发生在中心部位,边界附近的弯曲应变也很小。不同之处在于,叠层板沿x轴方向整体的弯曲应变水平较单层板要小得多,这主要是由于叠层板各层的厚度较小所致。
图13为叠层板沿对角方向(即组2)各单元的应变分布情况。比较图13a和图11a可知,叠层板沿对角方向各单元的薄膜拉伸应变分布较单层板要均匀,边界附近的薄膜拉伸应变较单层板要大,但中心部位的最大薄膜拉伸应变较单层板要小。图13b为叠层板对角方向各单元的弯曲应变变化及分布情况。与叠层板沿x轴方向的弯曲应变分布(图12d)不一样的的是,对角方向上的弯曲应变虽然也呈现出波浪式的分布,但其在变化过程中以及最终稳定情形下,对角方向上的最大弯曲应变并不在叠层板的中心部位,且体现出较强的时间和位置敏感性。这正是由于叠层板在变形过程中,塑性铰线沿对角线方向由边界向中心运动所引起的[17]。进一步比较图13b和图11b可知,单层板对角线方向的弯曲应变没有像叠层板一样出现较大的时空敏感性,说明其对角线方向上塑性铰线的影响较小,而叠层板对角线上塑性铰线的影响较大。由此可得,叠层板对角线上的塑性铰线较单层板要明显,试验结果也证明了这一点。
5.4 变形吸能分析
由上节对叠层板和单层板应变分布的分析可知,叠层板的薄膜拉伸变形是主要的变形机理,弯曲变形很小且可忽略。由此可见,叠层板获得的绝大部分动能都将以薄膜拉伸变形的方式耗散掉。图14比较了仿真计算得到的试验工况下单层板和叠层板的整体变形吸能情况。由图可知,叠层板的整体变形吸能量要大于单层板,这主要得益于叠层板的薄膜拉伸变形分布较单层板要均匀。结合上节的应变分析可得,叠层板的整体变形吸能量较单层板要大,而其最大塑性应变较单层板要小。由此可见,近距空爆载荷下,叠层板的抗爆变形能力要明显优于相同材料和厚度的单层板。
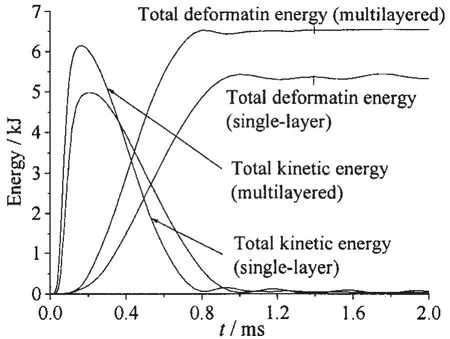
图14 变形吸能比较Fig.14 Comparison of deformation energy absorption
6 极限应变状态下叠层板的变形吸能分析
通过对试验工况下叠层板抗爆机理的分析可看出,试验工况下叠层板和单层板的最大应变均远小于材料的失效应变,即试验工况下叠层板和单层板均远未达到结构失效破坏时的临界状态(即极限应变状态)。而工程实际中,设计者们可能更为关心的是极限应变状态下叠层板的变形吸能情况。因此,本文在对试验工况仿真的基础上,通过增加药量,使叠层板和单层板达到各自的极限应变状态。由于仿真计算中很难控制药量使结构刚好达到极限应变状态,因此本文仿真计算的极限应变工况中叠层板和单层板的最大应变在0.40至0.41之间。图15给出了相应的极限应变状态下,叠层板和单层板沿x轴方向(组1)单元的应变分布比较,叠层板的应变取的是相应位置处四层板单元的平均应变值。考虑到极限应变状态下单层板的弯曲效应较明显,因而此节比较的是叠层板和单层板各自单元的有效塑性应变值εeq。从图15中可看出,叠层板的应变分布明显较单层板要均匀得多。计算结果显示,极限应变状态下,叠层板的薄膜拉伸应变较单层板要大且分布更为均匀,而单层板的弯曲应变较大,尤其在边界部位及其附近表现得更为明显。而正是由于边界单元弯曲应变较大,使得单层板沿x轴方向单元的有效塑性应变并未呈现单调递减的变化趋势。如图15所示,尽管单层板的最大有效塑性应变仍位于中心点处,但边界处的有效塑性应变并不是最小。
结合对图15应变分布的分析可知,叠层板中心部位以外的区域有效塑性应变较大且分布较为均匀,应变梯度较小,这说明抗爆过程中叠层板的整体变形吸能能力发挥得更为充分。而计算结果显示,叠层板的有效塑性应变中薄膜拉伸应变较弯曲应变要大得多,这说明叠层板主要通过薄膜拉伸变形进行吸能,图16为极限应变状态下,叠层板和单层板的总体变形吸能比较。由图可知,叠层板的总体变形吸能较单层板要大得多。从具体总吸能量来看,叠层板的总变形吸能较单层板约大65.1%。由此可见,极限应变状态下,叠层板的变形吸能能力较单层板有很大提高。应该指出的是,叠层板的极限应变计算工况中炸药的药量约为单层板计算工况的1.25倍,这说明极限应变状态下叠层板抗爆承受能力较单层板稍强。

图15 极限应变状态下应变分布比较Fig.15 Comparison of strain distributions underultimate strain conditions
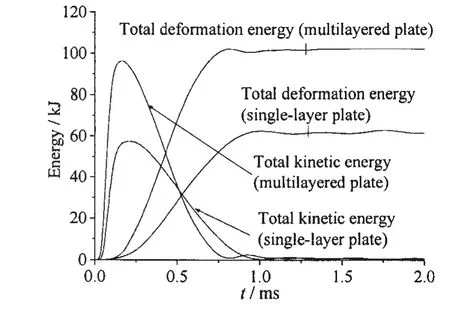
图16 极限应变状态下变形吸能比较Fig.16 Comparison of deformation energy absorptions under ultimate strain conditions
7 叠层板抗爆性能影响因素分析
7.1 层间间距影响
结合模型试验工况,进一步分析了层间间距对叠层板应变分布的影响。图17为在模型试验工况2下,叠层板层间间距的变化对其应变分布的影响。需要说明的是,此处分析的层间间距是指各层层间间距相同的情形。通过5.3节对应变分布的分析可知,弯曲应变很小且可忽略,因此此处只分析叠层板第4层的薄膜拉伸应变,取叠层板第4层沿x轴方向(组1)单元εmidy应变进行分析。由图17可看出,随层间间距的增大,叠层板第4层的应变不断减小,且边界附近应变减小较明显。这是由于,一方面结合5.1节爆炸载荷的分析可知,层间间距的增大能在一定程度上减小反射冲击波的峰值压力;另一方面,层间间距的增大使得传递至叠层板背层的动量减小。图18给出了叠层板层间间距为5 mm的情形下,各层的应变分布情况。由图可知,虽然叠层板第4层的应变有所减小,但其第1层的应变却明显增大,且各层之间应变梯度较大。这显然是由于过大的层间间距不利于叠层板各层之间的协调变形所致。
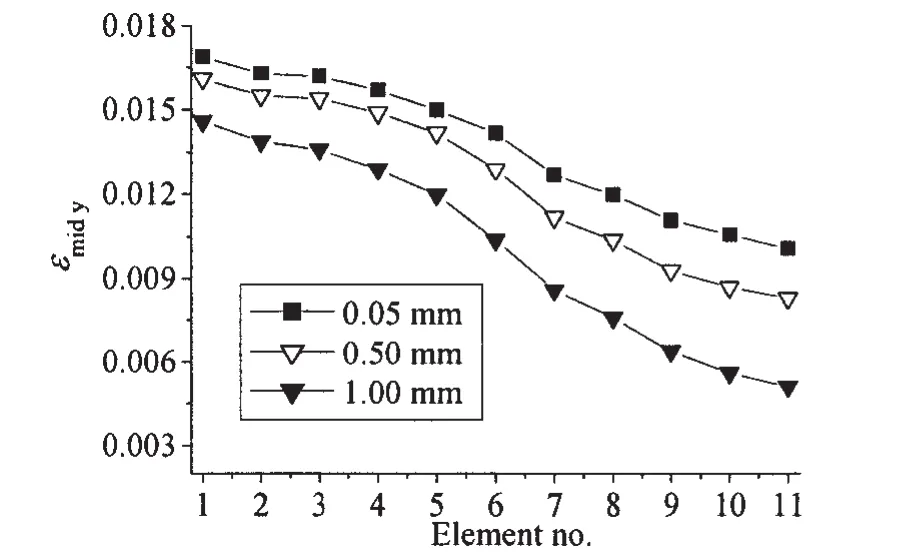
图17 不同层间间距下叠层板(第4层)的应变分布Fig.17 Strain distributions of the multilayered plates(the 4th layers)with different interlayer spaces

图18 层间间距为5 mm时叠层板各层的应变分布Fig.18 Strain distributions of the layers in the multilayered plate with 5mm interlayer space
通过以上分析可得,一定载荷工况下,在一定范围内,适当地增大叠层板的层间间距能减小其背层的应变大小;但过大的层间间距不利于叠层板整体协调变形,从而不能充分发挥其抗爆变形能力。
7.2 叠层层数影响
图19给出了相同总厚度下,具有不同层数(4、6和8层)叠层板背面最后一层沿x轴方向(组1)单元在t=2.0 ms时刻εmidy应变的分布情况,该时刻各叠层板塑性变形均趋于稳定。由图可知,在相同近爆工况下,柔性叠层板结构的层数越多,其最大应变越小,应变分布越均匀,说明其抗爆变形能力越强。然而当层数过大时(在本计算工况下为大于4层),其应变减小的幅度相对变小,这说明过多的层数对于叠层板抗爆变形能力的提高并不明显。由于叠层板主要是通过减小各层板的弯曲应变,提高其薄膜拉伸变形能力来提高其整体抗爆变形能力的,因此过多的层数对于叠层板各层弯曲应变的减小以及薄膜拉伸变形能力的提高效果并不明显。考虑到工程实际中,层数越多其施工工艺越复杂,因此叠层板层数的选取不宜过多。

图19 叠层板的层数对其应变分布的影响(t=2.0 ms)Fig.19 Effect of layer number on the strain distributions of the multilayered plates(t=2.0 ms)
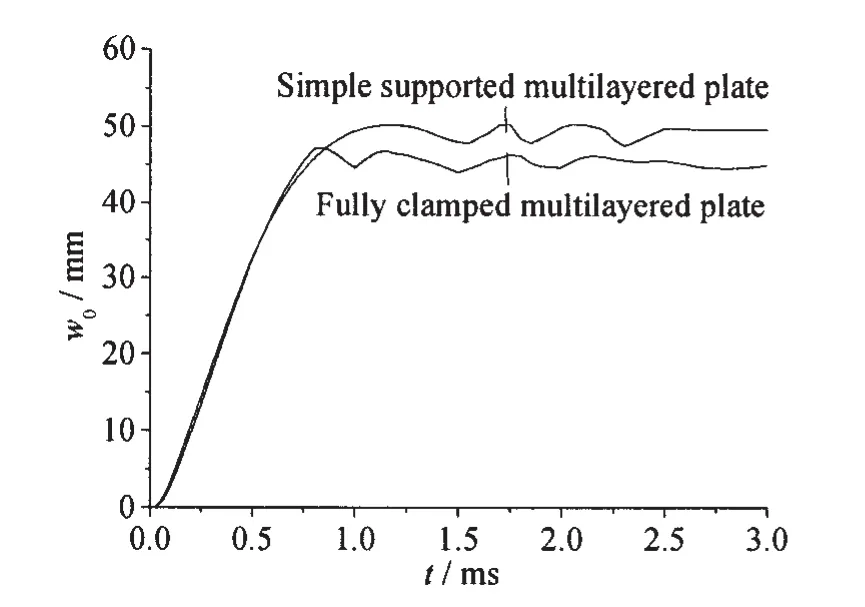
图20 边界条件对叠层板位移时程的影响Fig.20 Effect of boundary conditions on displacement histories of multilayered plates
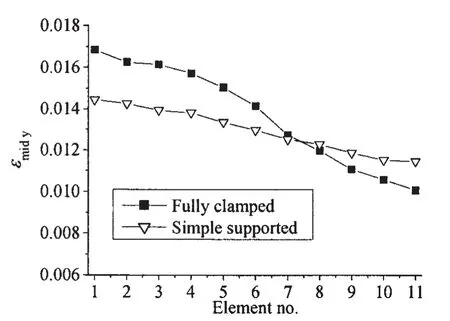
图21 边界条件对叠层板应变分布的影响(t=1.5 ms)Fig.21 Effect of boundary conditions on strain distributions of multilayered plates(t=1.5 ms)
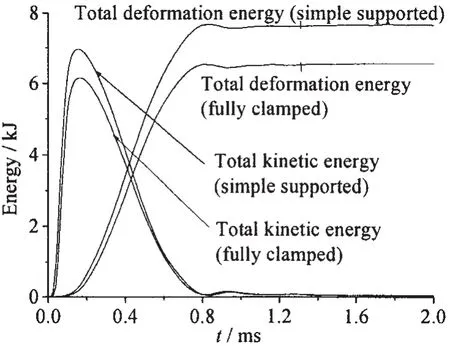
图22 边界条件对叠层板(4层)吸能的影响Fig.22 Effect of boundary conditions on energy absorptions of multilayered plates(4 layers)
7.3 边界条件影响
为进一步分析边界条件对叠层板抗爆性能的影响,对试验工况2叠层板在简支边界条件下的情形进行了仿真计算,并与固支边界条件下的计算结果进行了比较。图20和21分别为两种边界条件下叠层板位移时程曲线和变形吸能曲线的比较,其中图20叠层板的位移均取的是四层板中心点处位移w0的平均值。图21均取的是叠层板第4层沿x轴方向(组1)单元t=1.5 ms时刻εmidy应变值。由图20可看出,简支边界条件下叠层板中心点处的最终位移要大于固支边界的情形,由此可见简支边界条件下叠层板的整体变形程度较固支边界要大。然而,从图21中的应变分布情况来,简支边界条件下叠层板的最大应变并不比固支边界的大。从图21中可看出,简支边界条件下叠层板边界附近的应变较固支边界要大,然中心点处的应变较固支边界要小,从而使得简支边界条件下叠层板的应变分布较固支边界要更为均匀,整体抗爆变形能力能得到更有效地发挥。从图21中还可看出,由于本文所研究的叠层板的尺寸相对较大,因而其最大应变仍发生于中心点附近。若叠层板的尺寸相对较小,则简支边界条件下其最大应变有可能首先产生于边界中点附近,从而会出现如文献[9]中得到的沿边界拉伸撕裂的失效破坏模式。图22为简支和固支两种边界条件下叠层板的变形吸能情况比较。通过比较可知,简支边界条件下叠层板的整体变形吸能量较固支边界大约17%。由此可见,相同近距空爆载荷工况下,简支边界条件较固支边界而言,能较大程度地提高叠层板的抗爆吸能能力。结合图21对应变分布的分析可知,这是由于简支边界条件下叠层板整体变形程度较大且应变分布较均匀,因而能更好地发挥叠层板的薄膜拉伸变形吸能能力。
8 结论
结合模型试验,采用有限元对固支大尺寸叠层方板在近距空爆载荷作用下的抗爆机理进行了数值仿真分析,并与相同材料同等厚度的单层板进行了比较。最后,探讨了层间间距等因素对叠层板抗爆性能的影响。得到以下主要结论:
(1)相同的近距空爆载荷工况下,与同等总厚度的单层板相比,叠层板的变形吸能较大,但最大应变较小且应变分布更为均匀;而极限应变状态下叠层板的变形吸能较单层板要大得多,因而叠层板整体抗爆变形吸能能力明显优于单层板。
(2)一定范围内,适当地增大叠层板的层间间距能提高其抗爆变形能力,但过大的层间间距不利于叠层板的整体协调变形,从而不能充分发挥其整体抗爆变形能力。
(3)叠层板层数的增大对其整体抗爆变形能力的提高有一定效果,然而过多的层数对其抗爆变形能力的提高效果并不明显。
(4)较固支边界条件而言,简支边界条件能使叠层板的最大应变降低且应变分布更为均匀,因而能较大程度地提高叠层板的抗爆变形吸能能力。
[1]吴有生,彭兴宁,赵本立.爆炸载荷作用下舰船板架的变形与破损[J].中国造船,1995(4):55-61.
Wu Yousheng,Peng Xingning,Zhao Benli.Plastic deformation and damage of naval panels subjected to explosion loading[J].Shipbuilding of China,1995(4):55-61.(in Chinese)
[2]彭兴宁,聂武,严波.爆炸载荷作用下舰船防护舱壁的薄膜效应研究[J].船舶力学,2007,11(5):744-751.
Peng Xingning,Nie Wu,Yan Bo.Analysis of membrane effect of surface warship’s protective bulkhead subjected to blast loading[J].Journal of Ship Mechanics,2007,11(5):744-751.(in Chinese)
[3]Symond P S,Wierzbiki T.Membrane mode solutions for impulsively loaded circular plates[J].J Appl Mech,1979,46:58-63.
[4]Wierzbicki T,Nurick G N.Large deformation of thin plates under localised impulsive loading[J].Int J Impact Eng,1996, 18(7-8):899-918.
[5]Teeling-Smith R G,Nurick G N.The deformation and tearing of thin circular plates subjected to impulsive loads[J].Int J Impact Eng,1991,11(1):77-91.
[6]Nurick G N,Radford A M.Deformation and tearing of clamped circular plates subjected to localised central blast loads[C]// In:Recent Developments in Computational and Applied Mechanics.Barcelona,Spain,1997:276-301.
[7]Olson M D,Nurick G N,Fagnan J R.Deformation and rupture of blast loaded square plates-predictions and experiments [J].Int J Impact Eng,1993,13(2):279-291.
[8]Nurick G N,Shave G C.The deformation and tearing of thin square plates subjected to impulsive loads-an experimental study[J].Int J Impact Eng,1996,18(1):99-116.
[9]朱锡,冯刚,张振华.爆炸载荷作用下固支方板的应变场及破坏分析[J].船舶力学,2005,9(2):83-89.
Zhu Xi,Feng Gang,Zhang Zhenhua.Strain field and damage analysis of clamped square plates subjected to explosive loading[J].Journal of Ship Mechanics,2005,9(2):83-89.(in Chinese)
[10]Jacob N,Chung Kim Yuen S,Nurick G N.Scaling aspects of quadrangular plates subjected to localised blast loads-experiments and predictions[J].Int J Impact Eng,2004,30(8):1179-1208.
[11]Chung Kim Yuen S,Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates. Part I:Subjected to uniform blast load[J].Int J Impact Eng,2005,31(1):55-83.
[12]Langdon G S,Chung Kim Yuen S,Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part II:Localised blast loading[J].Int J Impact Eng,2005,31(1):85-111.
[13]侯海量,朱锡,古美邦.爆炸载荷作用下加筋板的失效模式分析及结构优化设计[J].爆炸与冲击,2007,27(1):26-33.
Hou Hailiang,Zhu Xi,Gu Meibang.Study on failure mode of stiffened plate and optimized design of structure subjected to blast load[J].Explosion and Shock Waves,2007,27(1):26-33.(in Chinese)
[14]Nurick G N,Langdon G S,Chi Y.Behaviour of sandwich panels subjected to intense air blast-Part 1:Experiments[J]. Comp Struct,2009,91:433-441.
[15]Xue Z,Hutchinson J W.A comparative study of impulse-resistant metal sandwich plates[J].Int J Impact Eng,2004,30 (10):1283-1305.
[16]Zhu F,Zhao L M,Lu G X,et al.A numerical simulation of the blast impact of square metallic sandwich panels[J].Int J Impact Eng,2009,36(5):687-699.
[17]陈长海,朱锡,侯海量等.近距空爆载荷作用下双层防爆舱壁结构抗爆性能仿真分析[J].海军工程大学学报, 2012,24(3):26-33.
Chen Changhai,Zhu Xi,Hou Hailiang,et al.Numerical analysis of blast resistance of double-layer bulkhead structures subjected to close-range air blast[J].Journal of Naval University of Engineering,2012,24(3):26-33.(in Chinese)
[18]陈长海,朱锡,侯海量等.近距空爆载荷作用下固支方板的变形及破坏模式[J].爆炸与冲击,2012,32(4):368-375.
Chen Changhai,Zhu Xi,Hou Hailiang,et al.Deformation and failure modes of clamped square plates under close-range air blast loads[J].Explosion and Shock Waves,2012,32(4):368-375.(in Chinese)
[19]Vaziri A,Hutchinson J W.Metal sandwich plates subject to intense air shocks[J].Int J Solids Struct,2007,44(6):2021-2035.
[20]Kambouchev N,Noels L,Radovitzky R.Numerical simulation of the fluid-structure interaction between air blast waves and free-standing plates[J].Comput Struct,2007,85(11-14):923-931.
[21]白志海,蒋志刚,严波等.金属加筋板局部爆炸冲击荷载研究[J].振动与冲击,2011,30(12):93-97,194.
Bai Zhihai,Jiang Zhigang,Yan Bo,et al.Localized blast loading of a stiffened metal plate[J].Journal of Vibration and Shock,2011,30(12):93-97,194.(in Chinese)
[22]Hanssen A G,Enstock L,Langseth M.Close-range blast loading of aluminium foam panels[J].Int J Impact Eng,2002, 27(6):593-618.
Numerical analysis of the blast-resistant mechanisms of multilayered thin plates under close-range air blast load
LIU Yan-honga,CHEN Chang-haib,ZHU Xib,LI Wanc,HOU Hai-liangb,TANG Tingb
(a.College of power engineering;b.Department of Naval Architecture Engineering;c.Department of Weapon Engineering,Naval University of Engineering,Wuhan 430033,China)
To explore the blast-resistant mechanisms of large-scale multilayered thin plates subjected to close-range explosions of warheads,finite element simulations as well as model tests were carried out.Blast loads,deformation processes,strain distributions and deformation energy absorptions of the clamped multilayered square plates under close-range air blast loads were numerically analyzed.Comparisons between multilayered plates and single-layer plates of the same materials and equal total thicknesses were conducted. On the basis of the numerical analysises,further investigations into the influences of interlayer spaces,layer numbers and boundary conditions on the blast resistances of multilayered plates were performed.The results show that under model test conditions,multilayered plates absorb more deformation energy than their monolithic counterparts,whereas their maximum strains are smaller,and strain distributions are more uniformly than those of the monolithic counterparts.Under ultimate strain conditions,a significant enhancement in deformation energy absorptions is obtained for multilayered plates comparing with their monolithic counterparts.Appropriate increase of interlayer spaces leads to a certain extent enhancement in deformation capabilities for multilayered plates,while overlarge interlayer spaces are unfavourable to their overallharmonious deformations.Deformation capabilities of multilayered plates are improved by increasing layer numbers.Comparing with clamped boundary conditions,simple-support boundary conditions are more conductive to the adequate exertion of deformation-energy-absorbing capabilities for multilayered plates.
explosion mechanics;close-range air blast load;multilayered thin plate; blast-resistant mechanism;numerical analysis
O344.7
A
10.3969/j.issn.1007-7294.2014.07.012
1007-7294(2014)07-0821-13
2014-05-04
国家自然科学基金项目(51179200,51209211)
刘燕红(1970-),女,博士,海军工程大学副教授,E-mail:LIUyhhg502@126.com;
陈长海(1985-),男,海军工程大学博士,讲师,E-mail:chenchanghai0746@163.com。

