平方阻尼在冲击隔离中的特性与作用研究

张春辉，赵建华，汪玉，谌勇

平方阻尼在冲击隔离中的特性与作用研究

张春辉1，赵建华1，汪玉2，谌勇3

（1海军工程大学动力工程学院，武汉430033；2海军装备研究院舰船所，北京100161；3上海交通大学振动、冲击、噪声国家重点实验室，上海200240）

传统的抗冲击设计认为阻尼对瞬时冲击的最大结构响应没有显著影响，因此在冲击隔离中，忽略阻尼效应，重点考虑选择合适的刚度。但实际应用研究表明，这类系统不能同时抑制相对位移幅值和绝对加速度幅值，无法满足船舶及其设备的抗冲击要求。针对这类问题，建立单自由度平方阻尼抗冲击系统模型，研究平方阻尼在冲击隔离系统中的特性和作用，结果表明：平方阻尼可以明显提升系统的冲击隔离效率，降低相对位移幅值；同等冲击条件下，含平方阻尼系统绝对加速度冲击响应幅值比线性阻尼系统响应幅值小；阶跃速度等效法不适宜计算平方阻尼冲击隔离系统的绝对加速度，但可以计算其相对位移。

冲击隔离；平方阻尼；缓冲系数；速度阶跃

1 引言

刚度和阻尼是冲击隔离中两个重要的因素。传统设计认为阻尼对瞬时冲击（十毫秒级）的最大结构响应没有显著影响，因此，阻尼在船舶设备冲击隔离中的研究应用一直没有得到充分的重视，即对于持续时间很短的冲击响应问题一般简化为无阻尼系统进行处理[1-2]。

近年来，随着大阻尼比阻尼器的出现和抗冲击技术的发展，越来越多的学者认识到阻尼在冲击隔离中的重要性。目前，已有多名学者对阻尼在隔振抗冲系统中的应用进行了研究[4]，如地震防护[5-7]、汽车座椅缓冲[8-9]、飞机起落架抗冲[10]等的设计。从研究对象上看，这些设计主要针对持续时间长或只关心抑制相对位移幅值的冲击隔离问题，对于船舶设备这类遭受像水下爆炸这种瞬时冲击（十毫秒级）的隔冲问题研究较少。从阻尼类型上看，这些研究主要对线性阻尼和库仑阻尼在冲击隔离中的应用进行研究，对于平方阻尼的冲击隔离问题研究较少。

平方阻尼是一种较高流速的剪切阻尼，一般由基于节流理论的油压减震器产生，通过活塞上的小孔节流作用形成的压力差来实现耗能[11]。美国的Balandin等人对具有指数规律特性的隔离器的参数进行优化，发现由线性刚度和平方阻尼组成的隔振器可以实现对冲击的极限保护能力，且可以保证被隔离体回到初始位置，可用来隔离重复作用的冲击载荷[12]。上海交通大学的丁旭杰等人[13]对含平方阻尼隔冲系统的抗冲击性能进行了优化研究，获得了系统达到最优抗冲击性能的条件。这些研究表明平方阻尼可以实现最优抗冲性能，为平方阻尼的实际应用奠定了理论基础。但为了简化问题，以上研究均将冲击激励等效为阶跃速度。从理论上讲，冲击系统的初始状态一般为静止状态，即初始速度为零，系统受冲击作用时必有一段时间处于加速阶段。速度阶跃等效法使系统一开始就获得初始速度，跨过了加速阶段，应该会影响计算结果。

基于以上原因，本文以船舶设备的瞬时冲击隔离问题为研究对象，应用数值模拟方法深入研究了平方阻尼在冲击隔离中的作用和可行性，并分析了速度阶跃等效法对冲击响应计算结果的影响。

2 平方阻尼冲击隔离模型的建立

含平方阻尼的冲击隔离系统如图1所示。设被隔离设备质量为m，弹簧的刚度为k，当在基础上施加冲击激励u¨（）t时，可以得到系统的运动方程：

式中：c为阻尼系数，x为质量块的绝对位移。令相对位移δ=x-u，此时冲击模型方程为：

图1 单自由度平方阻尼冲击隔离系统Fig.1 Single freedom system with quadratic damping

2.1 半正弦冲击模型

假设系统在零时刻受到半正弦波冲击

式中：A为冲击载荷幅值，t0为半正弦冲击持续时间，ωs为半正弦冲击的圆周频率。

2.2 速度阶跃冲击模型

当冲击持续时间t0远小于系统固有周期Tn时，常把冲击信号理想化为初始速度，即

定义频率比

则冲击模型（2）变为

冲击模型（4）和（6）均是非线性微分方程，无法给出直观的解析解。为了研究系统的响应特点，本研究采用龙格—库塔法进行数值模拟分析。

3 冲击响应的计算与分析

设冲击隔离系统遭受加速度峰值为50 g（1 g=9.8 m/s2），冲击作用时间为6 ms的半正弦激励。对不同频率比（1～20）和不同阻尼比（0～1）下的冲击模型（4）进行数值模拟，分析频率比和阻尼比对冲击响应的影响。

图3 频率比=2时加速度幅值出现时间与阻尼比的关系Fig.3 The occurrence time of absolute acceleration’s amplitude vs.damping ratio

图2 绝对加速度幅值随频率比和阻尼比的变化曲线Fig.2 Amplitude of absolute acceleration vs.damping ratio and frequency ratio

图4 最优阻尼比、等效阻尼比与频率比的关系Fig.4 The optimal and the equivalent damping ratio of absolute acceleration’s amplitude

图5 最优阻尼比、等效阻尼比时的冲击隔离率随频率比的变化曲线Fig.5 Shock isolation efficiency in the optimal and the equivalent damping ratio

3.1 绝对加速度响应幅值的计算与分析

不同频率比时绝对加速度响应幅值与阻尼比的关系曲线如图2所示，从图中可以看出，对于任意确定的阻尼比，频率比越大，绝对加速度幅值越小。在任意确定频率比下，绝对加速度幅值随着阻尼比的增加先减小后增大，存在一个阻尼比使得绝对加速度幅值最小，本研究定义该阻尼比为最优阻尼比。每条变化曲线（频率比γ=2除外）还存在一个阻尼比，使绝对加速度幅值等于阻尼比为零时的绝对加速度幅值，定义为等效阻尼比。

频率比γ=2时被隔离设备加速度幅值出现时间与阻尼比的关系如图3所示。从图中可以看出，阻尼比为0～0.17时，绝对加速度幅值均出现在冲击作用结束后。阻尼比为0.18～0.27时，绝对加速度幅值出现在冲击结束时刻，在此阶段平方阻尼耗散的能量比较接近，从而产生的加速度幅值大小相近。阻尼比为0.28～1.0时，绝对加速度幅值出现在冲击作用结束前，在加速度幅值出现之后的冲击能量被阻尼器吸收了，没有能量被继续输入到被隔离设备，因此，被隔离设备不会出现大于等于阻尼比=0时的加速度响应幅值，即频率比γ=2在阻尼比0～1之间不存在等效阻尼比。

最优阻尼比、等效阻尼比与频率比的关系如图4所示。从图中可以看出，平方阻尼隔冲系统的最优阻尼比为0.18，等效阻尼比随频率比的增大迅速减小，逐渐逼近阻尼比0.28。最优阻尼比、等效阻尼比时的冲击隔离效率随频率比变化曲线如图5所示，从图5可知，在小频率比时，使用最优阻尼比可以明显提升冲击隔离率；当频率比γ≥12后，最优阻尼比对冲击隔离效率的提升作用不再明显。

3.2 相对位移响应幅值的计算与分析

相对位移响应幅值随频率比和阻尼比的变化曲线如图6所示。由图可知，对于任意确定的频率比，相对位移响应幅值随阻尼比的增大而减小。对于任意确定的阻尼比，频率比越大，相对位移幅值越大。

图6 相对位移幅值随频率比和阻尼比的变化曲线Fig.6 Amplitude of relative displacement vs.damping ratio and frequency ratio

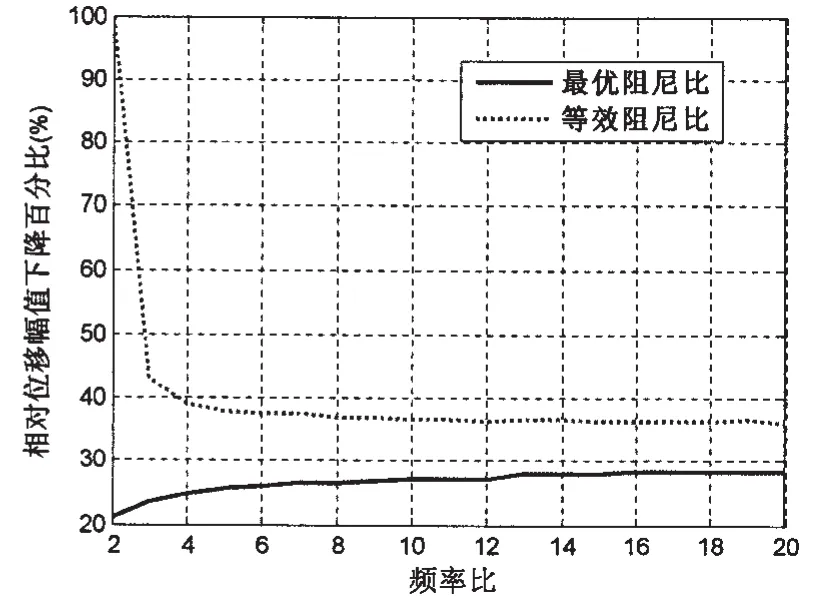
图7 最优阻尼比、等效阻尼比时相对位移幅值下降百分比Fig.7 The descend percent of relative displacement in the optimal and equivalent damping ratio

与无阻尼系统相比，最优阻尼比、等效阻尼比时的相对位移幅值下降百分比曲线如图7所示。从图中可以看出，最优阻尼比可以使相对位移幅值下降20%以上，等效阻尼比可以使相对位移幅值下降36%以上。因此，阻尼对于降低相对位移幅值效果明显。

3.3 平方阻尼对缓冲系数的影响

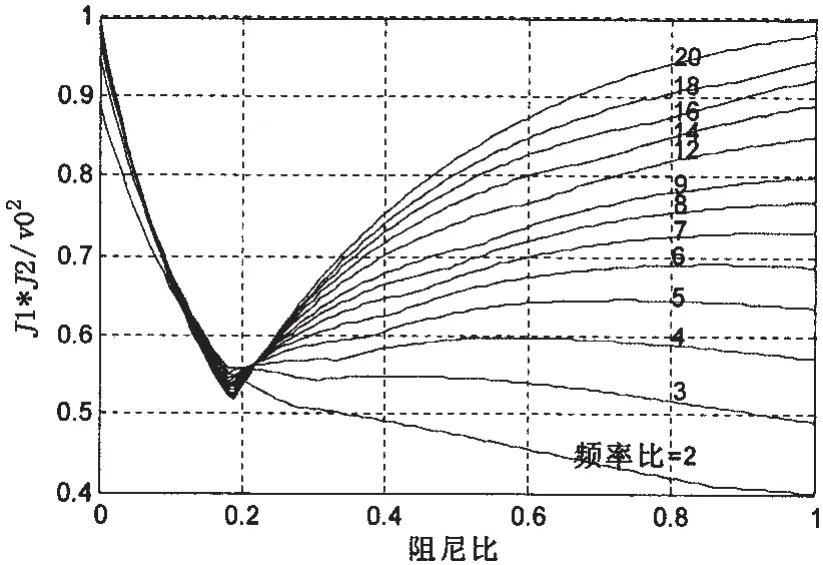
图8 不同频率比下系统缓冲系数随阻尼比的变化曲线Fig.8 The buffer coefficient vs.damping ratio and frequency ratio

冲击响应过程中，一般把设备绝对加速度响应幅值J1与相对位移响应幅值J2的乘积与阶跃速度v0的平方之比称为系统缓冲系数，用来表示系统的抗冲击极限性能，其值越小，表示系统抗冲性能越好。不同频率比下系统缓冲系数随阻尼比的变化情况如图8所示。从图中可以看出，对于γ＞3的任意确定的频率比，系统缓冲系数在最优阻尼比处取得最小值，即在最优阻尼比时，系统抗冲击性能达到最优。

3.4 冲击激励幅值对最优阻尼比的影响

取半正弦冲击加速度幅值为（10～100）g，研究最优阻尼比与冲击激励幅值的关系。首先运用龙格—库塔法计算每个冲击幅值下的最优阻尼比，然后运用指数拟合方法对所得计算值进行拟合。为了得到合理的拟合函数，对冲击激励幅值A进行无量纲化，令其中g为重力加速度，最优阻尼比ξ

与冲击激励幅值x的拟合函数为：

把冲击激励幅值x代入式（7）中可得最优阻尼比的拟合值，画出拟合曲线，结果如图9所示。从图中可以看出，拟合效果比较理想，最优阻尼比随冲击激励幅值的增加呈指数衰减。

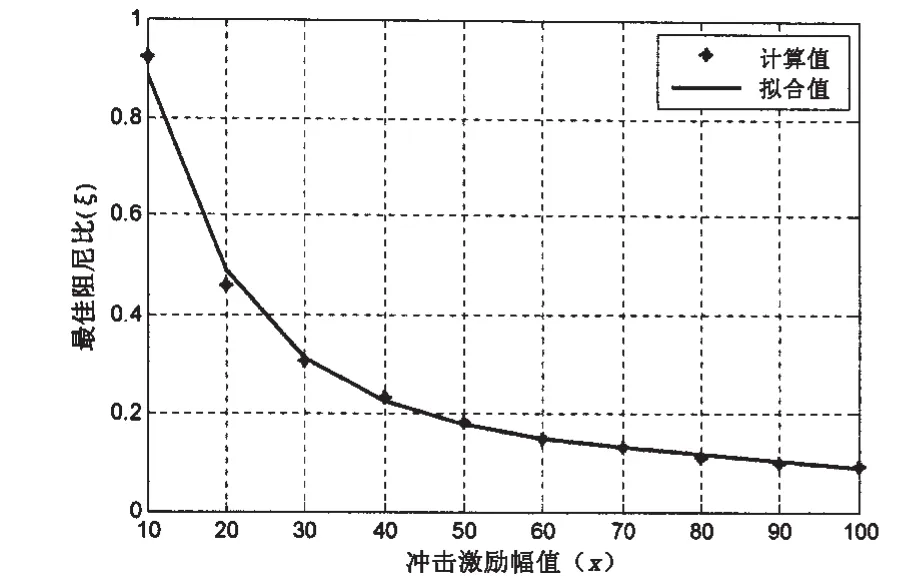
图9 最优阻尼比随冲击激励幅值的变化曲线Fig.9 The optimal damping ratio vs.the amplitude of impact load

图10 阶跃速度等效时绝对加速度幅值随频率比和阻尼比的变化曲线Fig.10 Amplitude of absolute acceleration vs.damping ratio and frequency ratio with velocity step equivalent

4 阶跃速度对冲击响应的影响

速度阶跃法可以把不同冲击持续时间的冲击信号等效为一个初始速度，在研究速度阶跃法的误差时，不同的冲击持续时间，速度阶跃法所导致的误差是不同的，所以必须对不同的冲击持续时间，即不同频率比进行研究。通过对不同频率比（1～20）和不同阻尼比（0～1）下的冲击模型（6）进行数值模拟，分析阶跃速度对冲击响应的影响。

图12 阶跃速度等效时系统缓冲系数随阻尼比的变化曲线Fig.12 The buffer coefficient vs.damping ratio and frequency ratio with velocity step equivalent

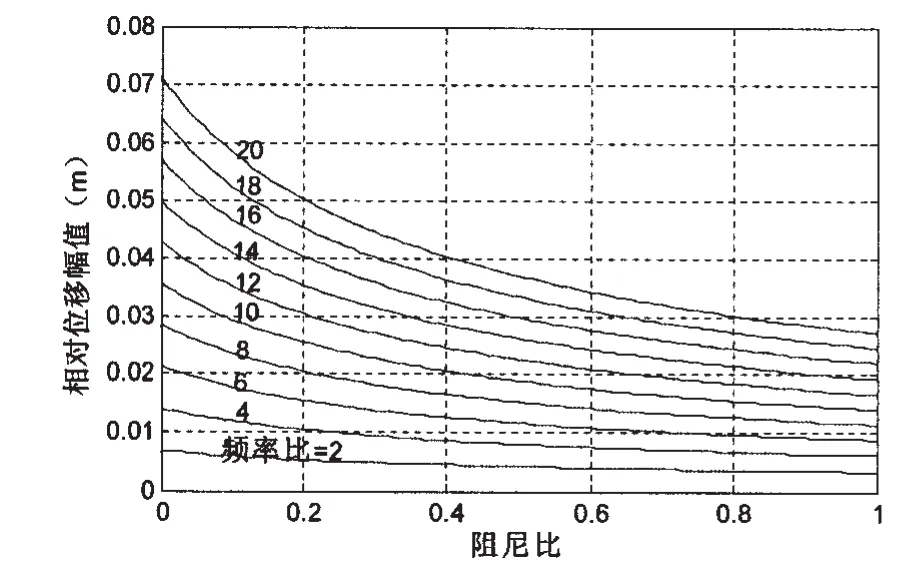
图11 阶跃速度等效时相对位移幅值随频率比和阻尼比的变化曲线Fig.11 Amplitude of relative displacement vs.damping ratio and frequency ratio with velocity step equivalent

图2、6和8的仿真结果没有进行阶跃速度等效，保存了系统的真实特性，可以将其作为其他仿真结果的标尺。阶跃速度等效时的冲击响应如图10、11和12所示。对比响应图10和图2，可以看出，当频率比γ＜12，阻尼比ξ＞0.25时，阶跃速度法计算的绝对加速度幅值已经严重偏离了真实值。因此，阶跃速度等效法不适宜计算平方阻尼隔冲系统的绝对加速度。对比图11和图6，发现阶跃速度等效法计算的相对位移幅值与真实值相符，没有误差。对比图12与图8，阶跃速度等效法计算的缓冲系数与真实的缓冲系数有明显的差异，这是由于误用阶跃速度引起的。

5 平方阻尼与线性阻尼的对比

为了分析平方阻尼的冲击响应特点，在相同的冲击环境下，对比分析了线性阻尼比ξ=0.18和ξ= 0，平方阻尼比ξ=0.18时单自由度隔冲系统的冲击响应结果。

图13为三种不同阻尼比时的绝对加速度响应对比图。从图中可以看出，相对于线性阻尼和无阻尼系统，含平方阻尼系统的绝对加速度响应幅值最小，主要是因为平方阻尼比在冲击响应的第一个极值处削平了加速度峰值，从而降低了绝对加速度响应峰值。图14为三种不同阻尼比下相对位移响应对比图。从图中可以看出，平方阻尼与线性阻尼的相对位移幅值大小基本相同，无阻尼系统的相对位移幅值最大。

图13 无阻尼、线性阻尼和平方阻尼时绝对加速度响应曲线Fig.13 The response of absolute acceleration for different types of damping ratio

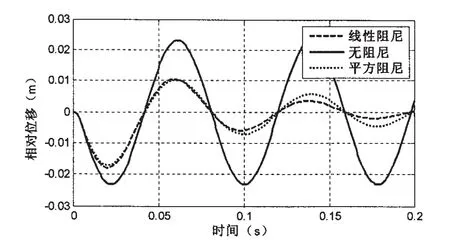
图14 无阻尼、线性阻尼和平方阻尼时相对位移响应曲线Fig.14 The response of relative displacement for different types of damping ratio

6 结论

对于线性刚度和平方阻尼并联组成的隔冲系统，可以得出以下结论：

（1）对于（γ＞3）任意确定的频率比，系统存在最优阻尼比，使设备绝对加速度响应幅值和系统缓冲系数同时取得最小值，且可以明显降低设备相对位移响应幅值；

（2）当阻尼比取等效阻尼比时，系统冲击隔离效率与无阻尼时保持相等，但相对位移响应幅值却比无阻尼时大幅下降；

（3）对于任意确定的阻尼比，系统频率比越大，绝对加速度响应幅值越小，相对位移响应幅值越大；

（4）系统最优阻尼比基本不随频率比的增大而变化，但随着冲击激励幅值的增加呈指数衰减；等效阻尼比随频率比的增加迅速减小，逐渐趋于阻尼比0.4；

（5）速度阶跃等效法不适宜计算绝对值加速度响应，但可以计算相对位移响应；

（6）在相同的冲击条件下，与线性阻尼系统相比，平方阻尼系统可以降低绝对加速度响应幅值。

[1]Scavuzzo R J,Henry C.Pusey.Naval shock analysis and design[R].The Shock and Vibration Information Analysis Center Booz Allen and Hamilton,inc.USA.2000:434-451.

[2]屈维德,唐恒龄.机械振动手册[M].北京:机械工业出版社,2000:700-750.

Qu Weide,Tang Hengling.Mechanical vibration handbook[M].Beijing:China Machine Press,2000:700-750.

[3]徐航田,单树军.粘性阻尼在软特性刚度隔冲系统中的作用研究[J].振动与冲击,2010,29(2):196-198.

Xu Hangtian,Shan Shujun.Effect of viscous damping in a soft stiffness shock isolation[J].Journal of Vibration and Shock, 2010,29(2):196-198.

[4]唐思密,朱石坚,楼京俊.半主动干摩擦阻尼器在隔振系统中的抗冲击优化设计研究[J].振动与冲击,2012,31(1): 11-15.

Tang Simi,Zhuhijian,Lou jingjun.Optimal shock isolation design for a vibration isolation system with a semi-active control dry friction damper[J].Journal of Vibration and Shock,2012,31(1):11-15.

[5]Mcmanus S J,Clair K A S T.Evaluation of vibration and shock attenuation performance of a suspension seat with a semiactive maghetorheological fluid damper[J].Journal of Sound and Vibration,2002,253(1):313-327.

[6]徐龙河,周云,李献忠.半主动磁流变阻尼控制方法的比较与分析[J].世界地震工程,2000,16(3):95-100.

Xu Longhe,Zhou Yun,Li Xianzhong.Comparison and analysis of semi-active magnetortheological damping control method [J].World Information on Earthquake Engineering,2000,16(3):95-100.

[7]Laura M J,Shirley J D.Semi-active control strategies for MR Dampers:Comparative study[J].Journal of Engineering Mechanics,2000,8:795-803.

[8]Sapinski B,Rosol M.Real-time controllers for MR seat damper[J].Smart Materials and Structures,2003,3:181-194.

[9]Mehdi A,James A N.Rheological controllability of double-ended MR dampers subjuected to impact loading[J].Smart Structures and Materials,2004,5386:185-194.

[10]Mikulowski G,Holnicki-Szulc J.Adaptive aircraft shock absorbers[J].AMAS Workshop Materticals and Structures,2003 (3):63-72.

[11]何玲.流体阻尼器特性及其对整星隔振性能影响的研究[D].哈尔滨:哈尔滨工业大学,2007:1-30.

He Ling.Characteristic of fluid damper and its effect on the whole-spacecraft vibration isolation[D].Harbin:Harbin Institute of Technology,2007:1-30.

[12]Balandin D V,Bolotnik N N,Pilkey W D.Optimal protection from impact,shock and vibration[M].Gordon and Breach, N J,1999.

[13]丁旭杰.非线性隔振抗冲器的设计与建模研究[D].上海:上海交通大学,2008:52-60.

Ding Xujie.Study on the design and modeling of nonlinear vibration and shock isolator[D].Shanghai:Shanghai Jiao Tong University,2008:52-60.

Effect of quadratic damping in a shock isolation system

ZHANG Chun-hui1,ZHAO Jian-hua1,WANG Yu2,CHEN Yong3
(1 Naval University of Engineering,Wuhan 430033,China;2 Naval Academy of Armament,Beijing 100161,China; 3 Shanghai Jiao Tong University,Shanghai 200240,China)

It is considered that damping has not significant effect on structure’s maximum response when the structure is suffered from a short time shock in the conventional shock isolation design.Therefore,a traditional shock isolation system is often designed on the selection of appropriate stiffness and ignoring the damping effect,which could not restrain both the absolute acceleration maximum and the relative displacement amplitude at the same time.This shock isolation system could not meet the shock isolation requirements of ships.A single-degree-of freedom quadratic damping shock isolation system model is built here.Effect of quadratic damping in a shock isolation system is studied by numerical simulations.It is indicated that using quadratic damping can obviously improve its shock isolation performance and reduce the relative displacement amplitude.Quadratic damping shock isolation system can obtain smaller response amplitude than linear damping system under the identical shock conditions.Velocity step equivalent method is not suitable for the calculation of absolute acceleration shock isolation system,but it can calculate the relative displacement.

shock isolation;quadratic damping;buffer coefficient;velocity step

O322

A

10.3969/j.issn.1007-7294.2014.07.013

1007-7294（2014）07-0834-07

2013-11-18

国防973项目（613157010102）；国防十二五预研基金（4010304030202）；

海军工程大学青年基金（HGDQNJJ12007）

张春辉（1988-），男，海军工程大学博士研究生，E-mail：502773429@qq.com；

赵建华（1975-），男，博士，海军工程大学副教授。