结构外声场的映射变阶波包络无限元法

苏楠，庞福振，姚熊亮

结构外声场的映射变阶波包络无限元法

苏楠，庞福振，姚熊亮

（哈尔滨工程大学船舶工程学院，哈尔滨150001）

基于径向形函数可任意变阶的映射波包络声学无限元法，以无限长圆柱壳体为研究对象，用数值计算方法对其结构外声场进行研究分析，并与其解析解进行对比，结果表明：两者之间能够较好地吻合，从而验证了映射变阶波包络声学无限元法在计算结构声辐射中的可行性，且具有效率高、精度好等优点。在此基础上，本文还讨论虚拟极点位置对声辐射的影响，通过对比四极子极点偏心声压值发现：极点存在偏心时，对实际工程问题有不利影响，但随声学无限单元阶数的增加，误差会减小。

映射变阶波包络法；声学无限元；虚拟极点；声辐射

1 引言

计算结构外声场问题可归结为无界域声波波动方程的数值求解问题，如水下航行器的声辐射问题、机翼的流激噪声等。有限元法在求解此类问题时，计算量大且效率不高，并会带来较大的声学截断误差。因此，为了克服有限元法在求解无限域结构外声场问题时的不足，从而提出无限元法。

关于无限元法的相关问题研究国内外已有大量文献发表，其中具有代表性有：Bettess和Zienkiewicz[1-2]在研究表面水波和折射问题时首次提出了无限元的概念，将声学问题在无穷远处满足的解直接移植到人工边界上；并针对无限元的不足提出了一种映射无限单元，通过单元建立了局部坐标系与整体坐标系的映射关系，但在求解过程中碰到了从未定义过的指数型积分，在数学上没有严格的理论推导证明；Astley[3]依据Bettess[4]无限元思想提出了一种新的无限单元类型，这一单元类型中取权函数为形函数的复数共轭，运用Garlerkin加权残值法求解，该方法彻底消除了单元矩阵中的不确定积分，极大地简化了方程，而且系统矩阵中频率与刚度矩阵相互独立，从而可使用高斯积分对方程进行求解，后来此法被Cremers等人[5-7]将此声学无限元法发展成为径向方向可任意变阶的映射波络无限元法，并将几何映射函数和形函数分开处理。杨瑞梁[8-12]对声学无限元法的发展和研究进行了系统的阐述，同时对无限元法进行了详细地分类，从理论上分析了收敛性、条件数和角向量数对计算精度的影响。

在上述研究的基础上，本文基于径向方向任意变阶的映射波包络声学无限元法，较为详细地推导了系统矩阵平衡方程，并与解析法进行对比，验证了映射变阶波包络声学无限元法求解结构外声场的可行性，在此基础上，着重分析了虚拟极点偏心对声辐射计算精度的影响。

2 映射变阶波包络声学无限元法

本文基于径向形函数可任意变阶的声学无限元法，形函数沿两个方向相互独立构造：在径向上，采用任意阶数的拉格朗日多项式，从而实现了径向形函数的任意变阶；在横向上，保持形函数不变，这样可实现与低阶有限元的直接耦合。

图1 声场几何模型Fig.1 The geometry model of sound field

2.1 域内控制方程

考虑内边界为S1的无限大区域V，如图1所示。p（ x，t）为边界S1上的法向声压，假设该声波为一简谐波，p（ x，t）可表示为p（ x，t）=p（x） eiwt，它在声场域V内满足以下波动方程：

式中：V为外部无界区域，k=w/c为声学波数，▽2为拉普拉斯算子。在结构辐射表面S1应满足以下边界条件：

式中：U（）

x为法向振速。在无穷远处应满足Sommerfeld条件：

无限大外域声场问题可归结为求解边值问题（1）-（4）。

2.2 方程离散

为求解边值问题（1）-（4），引入较为简单的人工边界S2，将域V划分为内部区域V1和外部区域V2。在区域V1内采用常规的有限元法离散；在区域V2内采用无限单元离散，无限单元为向无限远延伸的四边形，如图2所示。此无限单元由一正方形母单元映射而来，节点1和2位于人工边界S2上，节点

式中：r为整体坐标系中坐标原点到区域V内一点的距离。

如果在远场边界S2上，S2距离振动体足够远，等效近似有限声学边界条件为：1、2、3、4分别对应母单元中的四个节点，其他两节点（1，1）和（1，-1）映射到无限单元的无穷远处。节点1′、2′与节点3、4关于节点1、2镜像。从局部坐标系ζ-ξ到整体坐标系x-y的映射函数为：

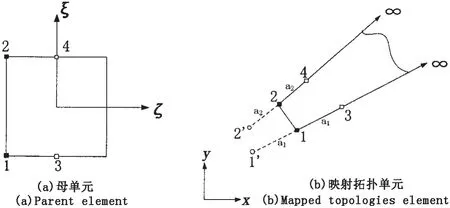
图2 映射波包络单元Fig.2 Mapped wave envelope element

式中：

沿着边1-3和边2-4的几何映射关系式可以表示为：

式中：r为沿1-3或2-4边距声源点1′或2′测得的距离。

2.3 单元系统矩阵

记Wi为权函数，Ni为形函数，对Helmholtz方程（1）应用Glerkin加权残值法，将在V上的体积分转化为在S1和S2上的面积分，得到等效的Helmholtz方程为：

同时，声学载荷量可以写成：

那么，系数qi表达式可以通过方程式｛q｝=（［K］+ik［R］-k2［M ］）-1｛F｝求出，其中：｛q｝为节点声压列向量，［K］为刚度矩阵，［R］为阻尼矩阵，［M］为质量矩阵，｛F｝为载荷向量列矩阵，k为声学波数。

形函数及权函数选取方法具体参考文献[6]。对于图2中的二维单元，各点的声压是基于几何节点1和2的声压值线性插值求得。波包络无限单元的插值函数Ni，其中包括模拟幅值衰减部分和声场中声压相位变化部分。对于n阶波包络法中仅考虑各自形函数下n个节点的声压，并认为第（n+1）个节点的声压值在无穷远处为零。

母单元中n阶多项式形函数采用拉格朗日多项式求得，其中n阶拉格朗日多项式由分列在几何节点之间的n个声学节点确定。n阶径向形函数可表示为：

通过使用局部映射函数ζ=ζ1+τh=τ/（n-1）-1，其中h=1/（n-1）。当ζ1=-1时，径向形函数可写成以下形式：

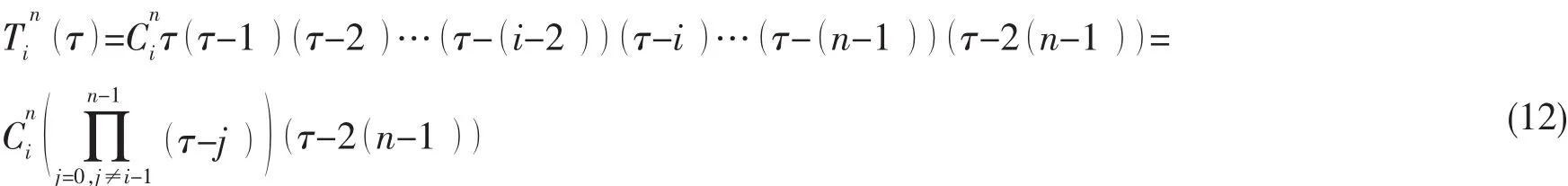
在母单元中使用此径向形函数映射到实际单元中为1/r的展开式，它适用于模拟三维或轴对称声波传播中的幅值衰减问题。但在二维声学问题中，声波幅值近似以形式衰减。对于二维问题，它的径向形函数由乘以系数因子相当于在母单元中乘以相应系数项。此时，二维径向形函数可以表示为：

在形函数中引入形如e-ikr的周期分量描述波形相位变化。为保证声学单元的连续性，在有限单元与无限单元的交界面ζ=-1处相位必须设定为零。因此，在局部坐标系中，相位变化可描述为：在二维声学无限单元中横向形函数可采用线性单元，不同边界对应的形函数为（如图2所示）：

相位函数μ（ ξ，ζ）可由极点位置a（ξ）插值得到，a（ξ）为如下表式：

从（16）式中可看出，向外传播的行进波是由在近场中的虚拟极点发散出来的，虚拟极点位于有限单元与无界单元的交界面a（）ξ处。将模拟声压幅值衰减函数和相位变化函数结合起来，给出n阶声学单元的形函数如下：

波包络法中权函数取为形函数的复数共轭乘以一加权因子（a/r）2，能保证无限单元中的刚度阵和质量矩阵的积分有限，同时能够满足无穷远处辐射条件。故权函数的表达式为：

其中几何权函数加权因子在局部坐标系中可表示为：

基于文献[6]可得到二维n阶无限波包络单元的刚度矩阵和质量矩阵的系数分别为：

单元矩阵中，复杂指数形式在被积函数中已被消除，故可采用数值高斯积分得到各个单元矩阵中的系数。单元矩阵中的各项系数经过组装得到系统矩阵，带入系统平衡方程即可求解得到所求节点声压值。

3 数值计算

3.1 映射变阶波包络声学无限元法有效性验证

基于映射变阶波包络声学无限元法理论，求解声压计算框图实现步骤见图3。为满足调整单元阶数的灵活性，即通过增加径向节点数目来实现声学无限映射单元中径向形函数的任意变阶。然而，母单元中任意增加节点数，必须保证映射到实际单元中时是沿着无穷远边界发散的，绝对不能出现交叉现象，即不存在当ζ∈[-1，1）时，通过方程（7）得到点的坐标不能位于1-4或2-3连线上。n阶声学映射无限元单元的位置是由它的四个几何节点和n阶径向插值形函数确定。在n阶无限单元径向上至少需要（n+1）个高斯积分点，横向方向上至少需要3个高斯积分点才能满足计算精度要求。

图3 无限元声压矩阵计算框图Fig.3 Acoustic infinite element pressure matrix computation block diagram

本文基于映射变阶波包络声学无限元法通过数值计算给出三维无限长刚性体运动的声辐射。取浸没在无限域流场的一个二维轴对称无限长圆柱壳体为研究对象，计算求解无限声场域中声压。将数值计算结果与文献[6]解析解对比来验证本文方法的有效性。以下所有算例中，声学介质密度为ρ= 1 024 kg/m3，声传播速度为c=1 500 m/s，如不作特殊说明，这些参数保持不变。

3.1.1 解析解

二维单极子、偶极子和四极子在柱坐标系中的声辐射解析解可表示为：

其中：V0为振速幅值，V0=1e-6 m/s。

3.1.2 数值解

在无量纲化参数ka=π a=1（）m下，偶极子、四极子声辐射在声场中的声压分布图如图4、图5所示。确定声学波数k使圆柱体直径2a对应一个波长。法向速度边界条件V0=1e-6 m/s。

由图4可知，通过将偶极子声辐射数值解与解析解对比发现二者吻合程度很好且计算效率高；随着波包络单元阶数提高，误差变得更小。由此可判定声学无限元方法能够很好地满足计算精度要求。

其中：Hn为第二类n阶汉克尔函数，n=0，1，2分别对应单极子、偶极子和四极子声辐射。

在无限长圆柱体振动表面的法向速度分布为：

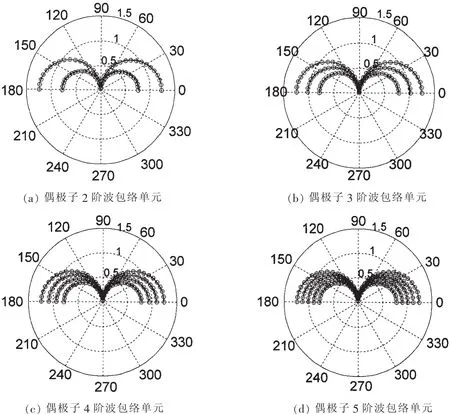
图4 振动圆柱体辐射声压（ka=π）-+-+-，解析解；-o-o-，数值解Fig.4 The radiated sound pressure of vibration cylinder(ka=π).-+-+-,analytical solution;-o-o-,numerical solution

图5 振动圆柱体辐射声压（ka=π）-o-o-，解析解；+*+*，数值解Fig.5 The radiated sound pressure of vibration cylinder(ka=π).-o-o-,analytical solution;+*+*,numerical solution

由图5可知，通过将四极子声辐射数值解与解析解对比发现二者吻合程度也很好；同时发现径向形函数的阶数越高，二者的吻合程度相当高。从偶极子和四极子算例中，分析发现将映射变阶波包络声学无限元法应用到求解结构外声场声压是可行的，且具有较高的精度。

3.2 虚拟极点位置对结构声辐射的影响

在映射波包络无限元法中，假设了一个在物理意义上不存在的虚拟声源（即极点），其中极点作为声源的扰动起点具有重要作用。一般来说，虚拟极点声源都放置在几何中心处，恰似结构的辐射声波从虚拟极点发出，但在实际工程问题中，很难满足这样的要求。因此有必要讨论虚拟极点位置对结构声辐射的影响。本节以简单声源（四极子）为例分析了虚拟极点位置对声辐射的影响。

在无量纲常数ka=π a=1（）m下，极点偏心距离取X=-0.5 m时，四极子声学无限元声辐射虚拟极点偏心与未偏心数值解对比如图6所示。

图6 虚拟极点位置对辐射声压的影响（ka=π）-+-+-，虚拟极点未偏心；-o-o-，虚拟极点偏心数值解Fig.6 The virtual sound source’s position influence on radiated sound pressure(ka=π).-+-+-,virtual sound source in center;-o-o-,numerical solution of virtual sound source with decentration

如图6所示，虚拟极点的位置不同对辐射声压的影响不同，通过对比四极子极点偏心声压值发现，当虚拟极点存在偏心时，对声压计算精度有不利影响。但随声学无限单元的阶数增加，误差会变小，其数值解会接近于真实解。因此，在实际工程问题中应增加声学无限单元的阶数来提高计算精度，控制虚拟极点的偏心距离来减小误差。

4 结论

本文基于映射变阶波包络声学无限元法，以无限长圆柱壳体为研究对象，将映射型声学无限元法与有限元法耦合求解无界域远场的辐射声压，提出了结构近场可用有限元模拟，远场可用声学无限元法离散的模型，运用映射型声学无限元法数值求解了研究对象的声辐射，与解析解对比验证了映射变阶波包络法的有效性，并进一步讨论虚拟极点位置对声辐射的影响。结论如下：

（1）在无限流场域中具有法向振速的结构外取一简单的人工边界，在人工边界内采用有限元离散求解边界节点信息，而在人工边界外敷设一层声学无限单元，在无限单元中通过耦合边界节点信息，从而采用径向映射变阶的波包络无限元法求解远场辐射声压。

（2）基于映射波包络无限元法的理论，通过数值计算对比验证了映射变阶波包络声学无限元法在计算结构外声场声压的有效性，分析发现映射变阶波包络声学无限元法具有较高的计算精度及求解效率；

（3）虚拟极点偏心对声辐射计算精度有较大影响，因此在实际工程问题中，应增加声学无限单元的阶数来满足计算精度要求，同时也要控制减小虚拟极点的偏心距离。

[1]Burnett D S.A three-dimensional acoustic Infinite Element based on a prolate spheroidal multipole expansion[J].Acoust. Sot.Am,1996.

[2]Bettess P.Infinite Elements[M].Penshaw,Sunderland,U.K,1992.

[3]Astley R J,Eversman W.Wave envelope elements for acoustical radiation in inhomogeneous media[J].Computers and Structures,1988,30(4):801-810.

[4]Burnett D S,Holford R L Prolate and oblate spheroidal acoustic infinite element[J].Comput.Methods.Appl.Mech.Engrg, 1998,158:117-141.

[5]Tsynkov S V.Numerical solution of problems on unbounded domains[J].A Review Applied Numerical Mathematics,1998, 27:465-532.

[6]Cremers L,Fyfe K R,Coyette J P.A variable order infinite acoustic wave envelope element[J].Sound Vib,1994,171 (114).

[7]Cremers L,Fyfe K R.On the use of variable order infinite wave envelope element for acoustic radiation and scattering[J]. Acoust.Soc.Am.,1995,97(4):2028-2040.

[8]杨瑞梁,汪鸿振.声无限元进展[J].机械工程学报,2003,39(11):82-87.

[9]杨瑞梁.声学无限元法的研究[D].上海:上海交通大学,2004.

[10]杨瑞梁,汪鸿振.声无限元进展[J].机械工程学报,2003,39(11):82-87.

[11]杨瑞梁,范晓伟.使用有限元和无限元耦合求解声辐射问题[J].振动工程学报,2004,17:1007-1009.

[12]杨瑞梁,汪鸿振.用长旋转椭球函数重构声场[J].噪声与振动控制,2003,5:15-17.

Variable order mapped wave envelope element of outer structural sound field

SU Nan,PANG Fu-zhen,YAO Xiong-liang
(Harbin Engineering University,Harbin 150001,China)

This paper is on the basis of a variable order in radial direction infinite acoustic wave envelope element(WEE).Numerical method is adopted to study the sound radiation pressure of an infinitely long cylinder as the subject investigated,and obtained results agree well with analytic solutions.The research presents that the variable order infinite acoustic wave envelope element which can be successfully applied to sound radiation pressure computation field is proven.The WEE has obvious advantages such as high efficiency and high degree of accuracy.Based on the above results,this paper also describes the influence of virtual sound source’s location in sound radiation,and it can be concluded that the decentration of virtual source has bad effects on the actual project by comparing the sound pressure values of quadrapole.However,with the increased orders of infinite acoustic element,the inaccuracy of sound pressure is decreasing.

variable order mapped wave envelope elements;infinite acoustic element; virtual sound source;sound radiation

O42

A

10.3969/j.issn.1007-7294.2014.07.016

1007-7294（2014）07-0856-08

2014-03-02

国家自然科学基金项目（51209052）；黑龙江省青年科学基金资助项目（QC2011C013）；哈尔滨市

科技创新人才研究专项资金项目（2011RFQXG021）；国防预研重点项目（401040XXX0103）

苏楠（1976-），女，硕士研究生，E-mail：sulanlan1988@126.com；

庞福振（1981-），男，博士，哈尔滨工程大学副教授。