SI-FLAT板形仪激振频率设定

杨光辉，张 杰，曹建国，黄桥宝，贾生晖

SI-FLAT板形仪激振频率设定

杨光辉1，张 杰1，曹建国1，黄桥宝1，贾生晖2

(1. 北京科技大学机械工程学院，北京 100083；2. 武汉钢铁(集团)公司冷轧厂，武汉 430083)

SI-FLAT板形仪是国内宽带钢冷连轧机首次采用的非接触式工业用板形仪，但实际使用过程中发现，对于常轧规格的带钢，其激振频率设定始终为同一固定值，激振力仅随张应力的变化而变化，导致板形控制不稳定，激振频率的设置严重影响着板形检测的精度．本文在分析现场实际生产数据的基础上，提出了激振频率的设置应该遵循的两个基本原则，即振幅控制原则和检测间隔控制原则．为了对带钢振动进行固有频率和受迫振动振幅的分析和计算，采用大型有限元软件ANSYS12.0建立了带钢振动仿真模型，分析了带钢板形、宽度、厚度、张应力等因素所导致的带钢固有频率波动对带钢振幅的影响．研究发现，张应力和板形对带钢固有频率的影响较大．最后，基于振幅控制原则和检测间隔控制原则提出了可行性方案，即通过限制最小张应力，减小板形对测量结果的影响；同时为了控制最小检测间隔，便于对板形的在线控制，激振频率的大小应根据带钢速度进行调节设定．

冷轧带钢；板形检测；激振频率；振幅；检测间隔

板带在生产过程中其操作环境十分恶劣，剧烈而复杂的振动以及水、油、灰尘等介质的侵入等往往会降低板形检测精度甚至会损坏检测装置．一般而言，板形检测的主要要求是高精度、良好的适应性、安装方便、结构简单、易于维护及对板带不造成任何损伤．因此，板形检测是一个比较困难的生产应用问题[1]．根据带钢和板形检测装置的相互接触关系，冷轧带钢板形仪可以归为两大类型：接触式和非接触式. 接触式板形仪由于与板带直接接触，检测到的板形信号比较直接，可靠度较高，测量得到的板形指标比较精确．但是接触式板形仪在检测过程中易划伤板带表面，造成新的缺陷，而且设备造价昂贵，维护较困难，严重影响生产．目前在冷轧带钢领域应用最为广泛的接触式板形仪是瑞典的ABB板形仪和德国的BFI板形仪．非接触式板形检测方法有很多，主要有气流激振-涡流测幅法、脉冲涡流测厚(测幅)法、次声级激振测频法、带振动能谱检测法等[2-9]，但真正研制成功并投入工业应用的并不多．其中，气流激振-涡流测幅法是目前应用最成功的方法，它的主要载体是德国西门子公司研制的SI-FLAT板形仪，目前已在武钢2,180,mm冷连轧机上得到了首次工业应用，并在国内外的其他生产线上逐步推广．由于该板形仪是首次工业应用，国内学者对其研究较少，板形仪的工业适应性有待进一步提高．本文结合冷连轧机组的实际生产情况，对SI-FLAT板形仪的激振频率的设定情况进行了研究分析．

1 激振频率实际设定情况

如图1所示，SI-FLAT板形仪通过对板带施加随时间呈正弦变化的激振力，使板带产生受迫振动，利用电涡流传感器测量出板带沿宽度方向做受迫振动的振幅，再通过振幅与板形(张应力)之间的转化模型，计算得到板带的板形[10-15]．通过上述工作原理可以看出，激振频率设定情况的合适与否，对板形检测的精度影响较大．

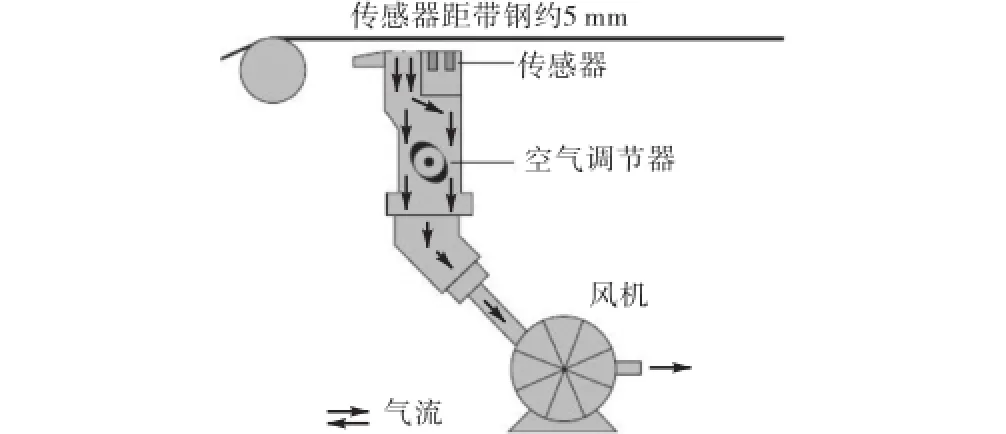
图1 SI-FLAT板形仪测量示意Fig.1 Measurement sketch of SI-FLAT shapometer

通过观察武钢2,180,mm冷连轧机大量的实际生产数据并分析发现，SI-FLAT板形仪激振频率的设置情况如图2所示．可以看出，对于常轧规格的带钢，激振频率均设定为同一个固定值，即5.105,Hz．同时，在轧制过程中，带钢的张应力和板形均出现较大变化，最大值为最小值的2倍之多；激振力的大小主要随带钢张应力的变化而变化，在图中带钢表现为前期带钢张应力下降，激振力也跟着下降，后期带钢张应力较为平稳，激振力也较为平稳．激振力会在某一个张应力范围内保持为一个固定值，而不会随着带钢板形等因素而变化．

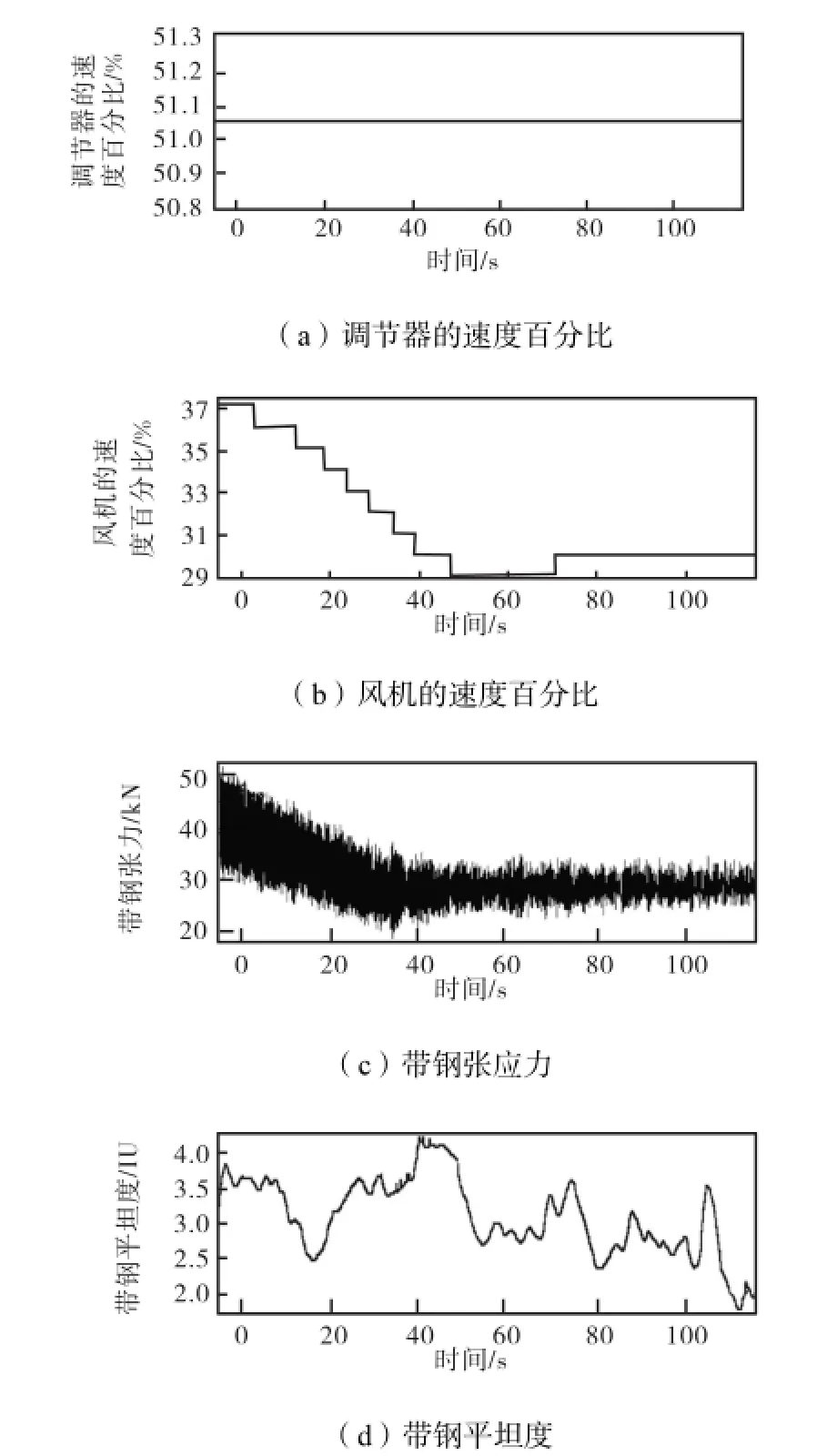
图2 典型生产信息Fig.2 Typical production information

2 激振频率设置的基本原则

结合SI-FLAT板形仪检测原理，本文提出了激振频率设定所应考虑的两个主要原则．

(1)振幅控制原则．在实际生产中，影响冷轧带钢固有频率的因素有很多，包括带钢的板形、张应力、厚度和宽度等．当激振频率设定为某一固定值时，若某些因素的变化导致带钢固有频率发生变化，则也将会使得带钢的受迫振动振幅出现一定程度的变化．而且，这种影响表现为激振频率离带钢固有频率越近，则在同等固有频率变化情况下所引起的带钢受迫振动振幅变化也就越大．而带钢的振幅如果变化过大，则可能会超出电涡流传感器的最佳测量范围，从而降低测量的准确度．因此，为了能将带钢的平均振幅控制在电涡流传感器的最佳测量范围内，需使得板形仪的激振频率离带钢固有频率的波动范围较远，这是进行激振频率设定时所应考虑的原则，本文将其称为“振幅控制原则”．

(2)检测间隔控制原则．电涡流传感器每隔一定的时间间隔对带钢的振动位移进行采样，同时，在经过一段时间的采样之后，需要对采样数据进行截断，以进行信号处理和板形计算、输出及控制．在已知带钢运行速度的情况下，截断周期的大小决定着板形仪相邻两次板形计算之间带钢运行距离间隔的大小．对于任一固定长度的单卷带钢而言，检测间隔越小，进行的板形调控次数就越多，越有利于板形质量的控制．

SI-FLAT板形仪利用气流的简谐激振力使带钢受迫振动，故带钢的受迫振动位移也表现为简谐形式．对于简谐振动而言，只有当截断周期至少大于简谐振动周期的一半时，才能保证采样得到的信号中含有简谐振动位移的峰值．而简谐振动周期又取决于激振频率，故激振频率的设定决定了板形仪理论上所能实现的最小检测间隔．因此，在进行激振频率设定时，需要考虑检测间隔这一因素．本文将该原则称为“检测间隔控制原则”．

3 带钢振动仿真模型

为了对带钢振动进行固有频率和受迫振动振幅的计算和分析，需要建立带钢振动仿真模型．带钢在SI-FLAT板形仪测量区域一端缠绕于导向辊上，一端夹在夹送辊之间，所以可简化为简支约束．在线冷轧带钢通常存在两个明显的特征：一是受到大张应力的作用，二是有沿带钢长度方向的运动．文献[16]的研究表明，运动速度对带钢固有频率的影响不大，可不考虑，而张应力对固有频率的影响较大．所以本文只考虑张应力的影响而不考虑运动速度的影响．此外，在带钢运动过程中作用于带钢的阻力主要是空气阻力，而由于带钢振动速度不快、振幅不大，空气阻力可以忽略[17-18]，故本文不考虑空气阻力的影响．因此，在线冷轧带钢可简化为对边简支、对边自由并承受张应力作用的薄板，如图3所示．

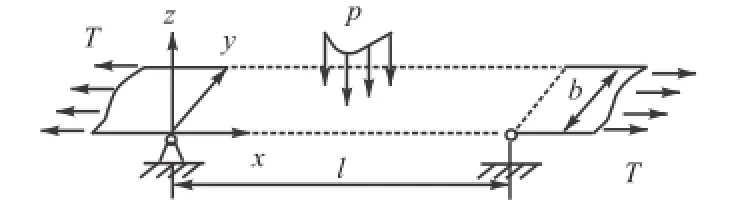
图3 在线冷轧带钢力学模型示意Fig.3 Sketch of mechanics model of cold rolled strip

本文利用大型有限元软件ANSYS12.0建立了带钢振动仿真模型，如图4所示．模型采用弹性壳单元shell63，4节点6自由度，不考虑剪切变形．其中模态分析模型的求解方法为分块兰索斯法，谐响应分析模型的求解方法为模态叠加法[19-20]．带钢弹性模量为2.1×1011,Pa，泊松比为0.3，密度为7,850,kg/m3[21-22].在进行受迫振动求解时，激振力均匀施加在x= 335,mm的节点上，振幅测量位置在x=410,mm的节点处．

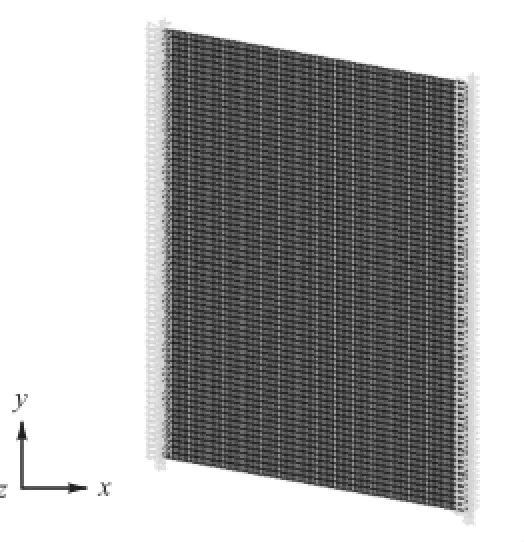
图4 带钢振动有限元仿真模型Fig.4 Finite element model of strip vibration

4 张应力和板形等因素对带钢固有频率的影响

通过带钢振动仿真模型，计算得到了带钢1阶固有频率随带钢板形、宽厚和张应力等因素的变化情况，如图5～图7所示．

图5分析的基本工况参数为带钢宽度为1,400 mm，带钢厚度为1.5,mm，张应力为40,MPa．由图5(a)可以看出，边浪、中浪、1/4浪、边中复合浪、无浪5种板形形式对带钢1阶固有频率的影响较大．在边浪的板形形式下，其1阶固有频率最小，约为33.379,Hz，在无浪的板形形式下，其1阶固有频率最大，约为39.682,Hz，增大了约18.9%．由图5(b)可以看出，带钢综合板形对带钢1阶固有频率的影响较大．带钢综合板形越大，其1阶固有频率越小，当综合板形为0I时，固有频率约为39.682,Hz，当综合板形为10I时，固有频率约为23.362,Hz，减小了约41.1%．可以看出，板形形式和板形的大小对带钢1阶固有频率的影响较大．

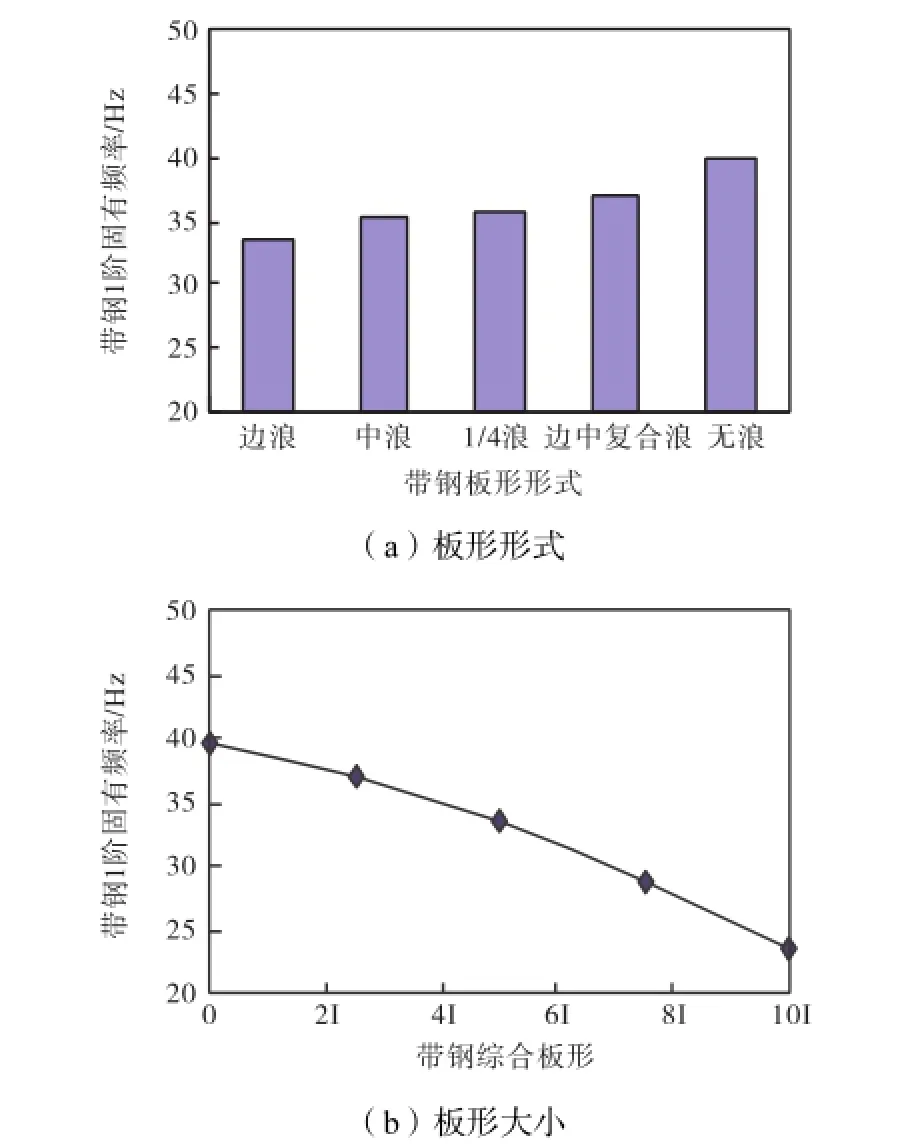
图5 带钢1阶固有频率随板形的变化情况Fig.5 Variation of the 1st natural frequency of strip with strip shape

图6 分析了带钢宽度为1,400,mm、厚度为1.5,mm、板形为无浪的情况下，带钢张应力在10～60,MPa范围内变化时，带钢1阶固有频率的变化情况．可以看出，张应力的大小对带钢1阶固有频率的影响很大．当带钢张应力为10,MPa时，其1阶固有频率约为20.210,Hz，当带钢张应力为60,MPa时，其1阶固有频率约为48.497,Hz，增大了约140%．

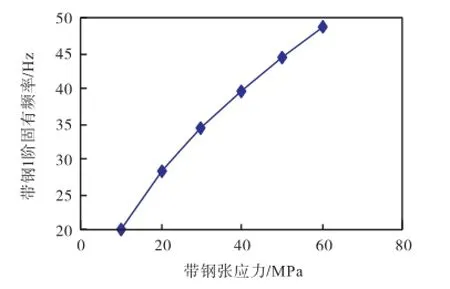
图6 带钢1阶固有频率随张应力的变化情况Fig.6 Variation of the 1st natural frequency of strip with the tensile stress of strip

图7 (a)分析了带钢厚度为1.5,mm、张应力为40,MPa、带钢宽度在800～2,000,mm范围内变化时，带钢1阶固有频率的变化情况．可以看出，带钢宽度对其1阶固有频率的影响很小．当带钢宽度为800,mm时，其1阶固有频率约为39.675,Hz，当带钢宽度为2,000,mm时，其1阶固有频率约为39.685 Hz，增大了约0.02%．图7(b)分析了带钢宽度为1,400,mm，张应力为40,MPa，带钢厚度为0.5～2.5,mm范围内变化时，带钢1阶固有频率的变化情况．可以看出，带钢厚度对其1阶固有频率的影响很小．当带钢厚度为0.5,mm时，其1阶固有频率约为39.393,Hz，当带钢厚度为2.5,mm时，其1阶固有频率约为40.121,Hz，增大了约1.8 %．

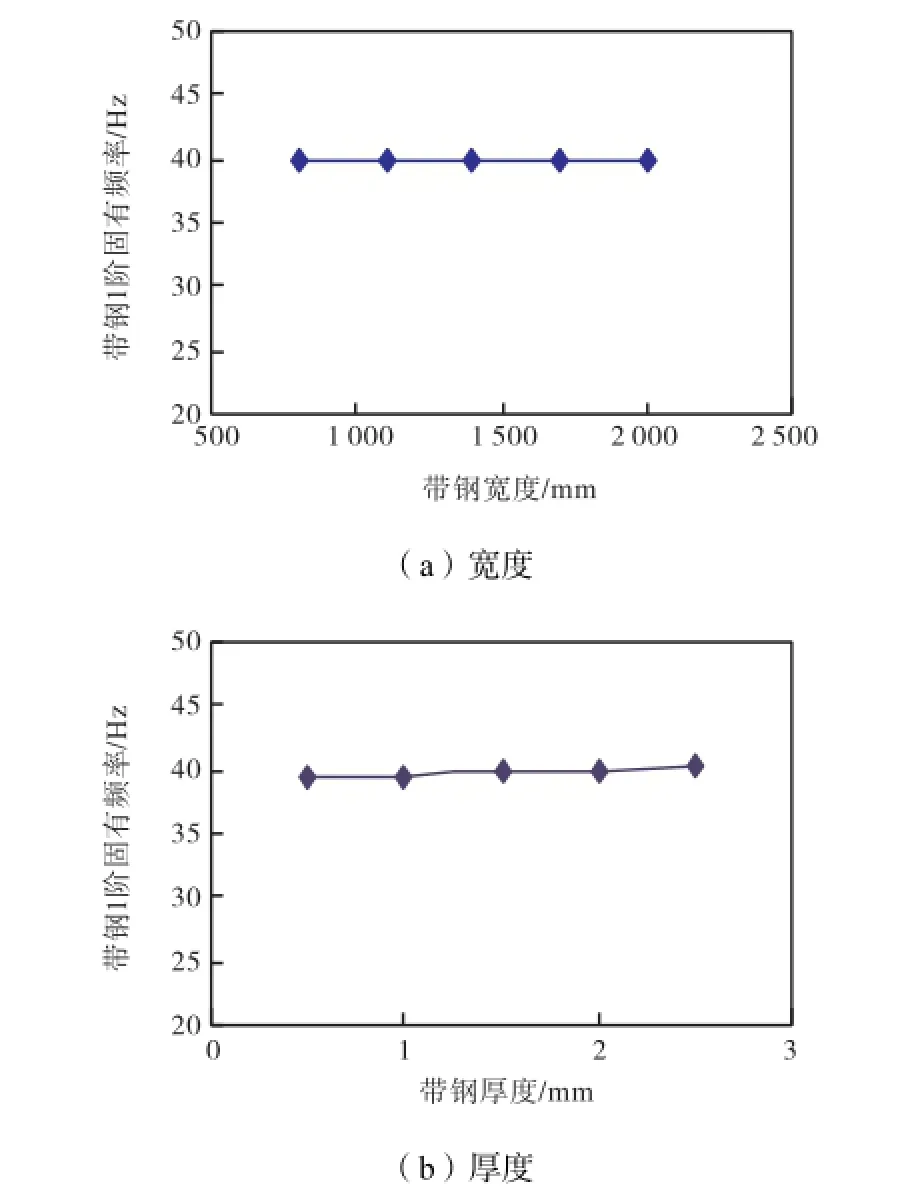
图7 带钢1阶固有频率随带钢宽度和厚度的变化情况Fig.7Variation of the 1st natural frequency of strip with the width and thickness of strip

5 激振频率设定情况的评价与分析

5.1 基于振幅控制原则的评价

可以看出，板形和张应力对带钢1阶固有频率的影响较大．而由激振频率实际设定情况分析可知，SIFLAT板形仪的激振频率设定为一固定值，激振力的大小仅随张应力变化而不随板形变化，这一定程度上影响了板形的检测精度．下面以1/4浪为例，对板形变化所造成的带钢整体振幅变化进行分析研究．

振幅控制原则主要分析的重点为激振频率与带钢固有频率波动范围之间的大小关系，以研究带钢板形、宽度、厚度、张应力等因素所导致的带钢固有频率波动是否会引起带钢平均振幅出现大的变化．因此，需首先研究生产过程中的各因素对带钢固有频率的影响情况．

图8(a)为综合板形为10I(1/4浪)与综合板形为0I(即无浪)的带钢的平均振幅比．可见，随着带钢张应力的减小，振幅比会增大，带钢振幅越来越难以保持相对稳定，这是因为带钢张应力越小，其固有频率与激振频率越接近，10I的综合板形变化对带钢振幅的影响就越大．可以看出，当张应力小于20,MPa时，板形影响已变得非常大，振幅比可达30多倍．因此，如果SI-FLAT板形仪的激振力仅根据张应力的变化来进行变化，而不考虑板形变化对振幅的影响，则当带钢张应力较小且板形波动较大时，SI-FLAT板形仪将难以使带钢振幅保持在一个相对稳定的范围内．

图8(b)为综合板形为7.5I与综合板形为2.5I的1/4浪带钢的平均振幅比．可见，当带钢张应力为20,MPa时，带钢的振幅比已达2.5左右，此时若将2.5I时的平均振幅设置为100,μm，则7.5I时已达250,μm左右，不能满足将带钢平均振幅控制在100～200,μm之间的要求；若带钢张应力小于20,MPa，情况将更加严重．

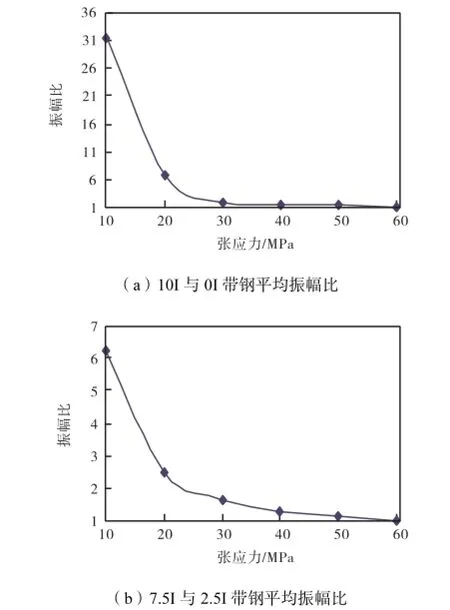
图8 不同板形大小之间的带钢平均振幅比Fig.8 Average amplitude ratio of strip for different flatness values

因此，对于SI-FLAT板形仪当前实际所设定的激振频率和所使用的振幅控制策略，随着带钢张应力的减小，其越来越难以在板形的同等变化程度下保持带钢振幅的相对稳定，当带钢张应力较小且板形波动较大时，带钢振幅会出现较大变化，可能会超出传感器的最佳测量范围，降低测量精度．所以，应限制最小带钢张应力，使这种情况得到一定程度的改善．5.2 基于检测间隔控制原则的评价

为了更好地进行评价分析，本文采用将SI-FLAT板形仪与BFI板形仪[23]的检测间隔进行对比分析．若BFI板形辊的直径为313,mm，每旋转一圈完成一次完整的板形检测，故BFI板形辊的检测间隔即为其圆周长度，即为982.82,mm．对于SI-FLAT板形仪，当激振频率为ωp时，激振周期为1/ωp，则截断周期dt应大于1/(2ωp)．将带钢运行速度用v表示，则SI-FLAT板形仪的检测间隔为

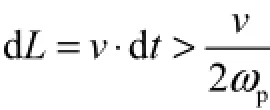
根据不同的带钢速度，SI-FLAT板形仪理论上所能实现的最小检测间隔如图9所示．可见，在固定激振频率的情况下，SI-FLAT板形仪所能实现的最小检测间隔随带钢速度呈线性变化规律，带钢速度越小，可实现的最小检测间隔也越小；对于某一固定速度下运行的带钢，通过增大激振频率，可以减小最小检测间隔．在当前的激振频率5.105,Hz下，当带钢速度小于10,m/s时，SI-FLAT板形仪所能实现的最小检测间隔小于BFI板形仪；当带钢速度大于10,m/s时，其所能实现的最小检测间隔则大于BFI板形仪，尤其是当带钢速度为20,m/s时，其最小检测间隔为BFI板形仪的2倍之多．所以，当带钢速度大于10,m/s时，相对于BFI板形仪，SI-FLAT板形仪的检测间隔要相对较大，不利于板形质量的控制，这一情况可以通过增大激振频率来改善．

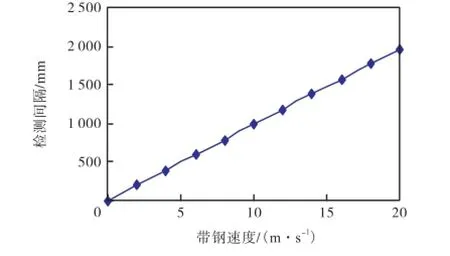
图9 SI-FLAT板形仪的最小检测间隔Fig.9 The minimum measurement interval of SI-FLAT

6 可行性分析

SI-FLAT板形仪在实际使用过程中，为了充分考虑张应力和板形对测量结果的影响，提高板形仪的测量精度，又便于现场在线应用，对于常轧规格的带钢，本文提出了基于振幅控制原则和检测间隔控制原则的SI-FLAT板形仪激振频率设置的可行性方案，其流程如图10所示，具体实施过程为：判断当前带钢张应力T与所限制的最小张力Tmin(Tmin=σminBh，σmin为所限制的最小张应力，B为带钢宽度，h为带钢厚度)之间的关系，可分3种情况讨论．

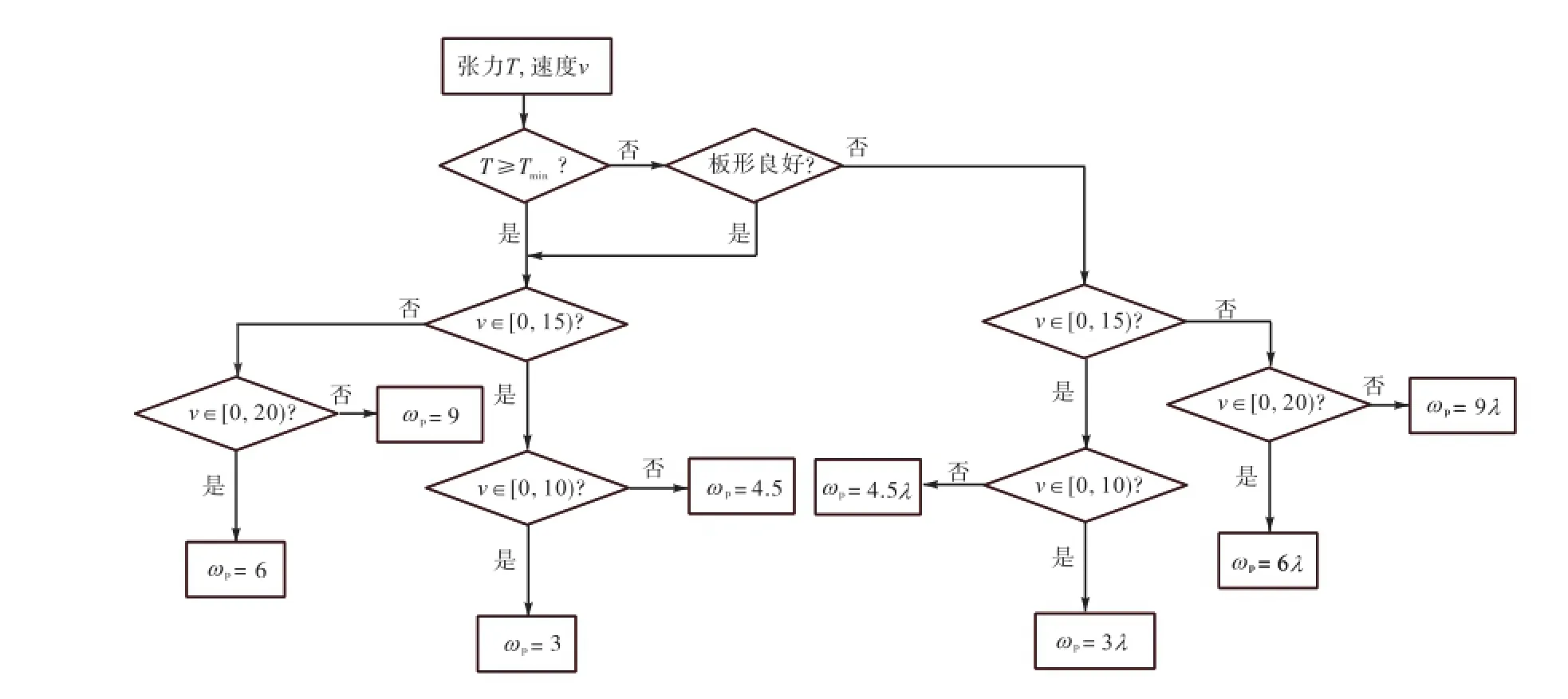
图10 激振频率设置流程Fig.10 Setting flow chart of excitation frequency

(1)当带钢张应力较大(T≥Tmin)时，板形对带钢固有频率影响较小，带钢振幅会在较为合理的范围内变化，满足测量条件要求；然后判断当前带钢速度位于哪个速度区段(见表1)，根据带钢速度来选择激振频率的设定值ωp．

(2)当带钢张应力较小(T＜Tmin)且板形波动较小时，带钢振幅会在较为合理的范围内变化，满足测量条件要求，可以根据带钢速度来选择激振频率的设定值ωp；

(3)当带钢张应力较小(T＜Tmin)且板形波动较大时，板形对带钢固有频率影响很大，带钢振幅会出现较大变化，并可能会超出传感器的最佳测量范围，降低测量精度，则激振频率的设定值应为正常情况下的设定值ωp乘以系数λ，λ取(0，1)，具体取值可根据实际生产情况来定．

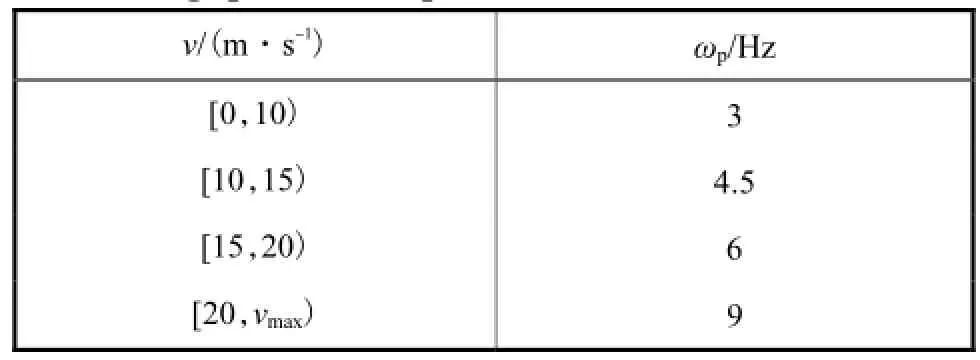
表1 激振频率随带钢运动速度的设置情况Tab.1 Setting of excitation frequency with different moving speeds of strip

7 结 论

(1)对于常轧规格的带钢，SI-FLAT板形仪的激振频率设置为同一个固定值，其所采用的振幅控制策略为：当带钢出现超出一定范围的张应力变化时，通过调节风机的转速来调节激振力的大小，从而达到使整体振幅保持相对稳定的目的；激振力大小的设置取决于张应力的大小，而不考虑板形等因素．

(2)基于现场实际生产情况，提出了激振频率设定应该遵循的两个原则，即振幅控制原则和检测间隔控制原则．为了对带钢振动进行固有频率和受迫振动振幅的研究，建立了带钢振动仿真模型，分析了多种因素所导致的带钢固有频率波动对带钢平均振幅的影响．研究发现，张应力和板形对带钢固有频率的影响较大，所以，当带钢张应力较小且板形波动较大时，带钢振幅会出现较大变化，带钢振幅可能会超出传感器的最佳测量范围，降低测量精度．

(3)基于振幅控制原则和检测间隔控制原则提出了可行性方案，即通过限制最小张应力，减小板形对测量结果的影响；同时为了控制最小检测间隔，便于对板形的在线控制，激振频率的大小应根据带钢速度进行调节．

参考文献：

［1］ 王国栋. 板形控制和板形理论[M]. 北京：冶金工业出版社，1986.

Wang Guodong. Profile Control and Profile Theory[M]. Beijing：Metallurgical Industry Press，1986(in Chinese).

［2］ 于丙强，杨利坡，孙建亮. 冷轧带钢板形检测辊研究现状[J]. 轧钢，2011，28(2)：44-46.

Yu Bingqiang，Yang Lipo，Sun Jianliang. Research status of shape detecting roller of cold rolled strip[J]. Steel Rolling，2011，28(2)：44-46(in Chinese).

［3］ 刘 浩. ABB板形测量系统在宝钢1,800,mm冷连轧机组的应用[J]. 冶金自动化，2006，30(1)：61-62.

Liu Hao. Application of ABB shape measurement system in Baosteel 1,800 mm cold rolling train[J]. Metallurgical Industry Automation，2006，30(1)：61-62(in Chinese).

［4］ Agureev V A，Kalmanovich E A，Kuryakin A V，et al. Use of gage IP-4 to measure the flatness of sheet on coldrolling mills[J]. Metallurgist，2007，51(5/6)：316-323.

［5］ 钟春生，岳利明，任明孝. 新的板形检测方法及其装置[J]. 钢铁，1995，30(1)：72-75.

Zhong Chunsheng，Yue Liming，Ren Mingxiao. New method and device for measuring flatness of sheet metal[J]. Iron and Steel，1995，30(1)：72-75(in Chinese).

［6］ 王快社，栾亚群. 采用激振测频法检测板形[J]. 新技术新工艺，2002(11)：16-17.

Wang Kuaishe，Luan Yaqun. Measuring the shape of strip with the method of measuring frequency by exciting vibration[J]. New Technology and New Process，2002(11)：16-17(in Chinese).

［7］ Aleksanyan G G，Sovlukov A S. Contactless lineardimension measurement with elevated sensitivity and accuracy[J]. Measurement Techniques，1986(5)：13-15.

［8］ Przywara J，Spreitzhofer G，Dummler A. Innovative contactless flatness measurement system for cold rolling reversing stands[C] //The 3rd European Rolling Conference Held in Conjunction with the 2003 METEC Congress. Dusseldorf，Germany，2003：57-60.

［9］ Sinha G，Prabhu S S . Analytical model for estimation of eddy current and power loss in conducting plate and its application[J]. Physical Review Special Topics—Accelerators and Beams，2011，14(6)：062401-1-10.

［10］ Spreitzhofer G，Duemmler A，Riess M，et al. SI-FLAT contactless flatness measurement for cold rolling mills and processing lines[J]. Revue de Metallurgie，2005，102(9)：589-595.

［11］ Spreitzhofer G. Non-contact measurement of strip flatness[J]. Steel Times International，2003，27(5)：16-17.

［12］ 杨光辉，张 杰，曹建国，等. 带钢非接触式平坦度检测原理及其检测系统[J]. 冶金自动化，2009(增1)：665-668.

Yang Guanghui，Zhang Jie，Cao Jianguo，et al. Principle and equipment of contactless strip flatness measurement[J]. Metallurgical Industry Automation，2009 (Suppl 1)：665-668(in Chinese).

［13］ 尹家勇. Si-Flat板形仪在六辊可逆铜轧机的应用[J].世界有色金属，2010(6)：46-47. Yin Jiayong. Application of Si-Flat in 6-h reversed copper mill[J]. World Nonferrous Metal，2010(6)：46-47(in Chinese).

［14］ 王明黔，王晓东. 非接触型板形仪Si-Flat的测量原理及应用[J]. 昆明冶金高等专科学校学报，2008，24(1)：34-36.

Wang Mingqian，Wang Xiaodong. Measurement principles and application of non-contact shape meter Si-Flat[J]. Journal of Kunming Metallurgy College，2008，24(1)：34-36(in Chinese).

［15］ 秦 政. 新型冷轧带钢板型仪SI-FLAT在冷连轧机的应用[J]. 冶金自动化，2004(2)：63-65. Qin Zheng. Application of new type shape meter SIFLAT in tandem cold mill[J]. Metallurgical Industry Automation，2004(2)：63-65(in Chinese).

［16］ 李 健，颜云辉，郭星辉，等. 基于薄板固有特性的连续热镀锌带钢表面质量在线控制[J]. 机械工程学报，2011，47(9)：60-65.

Li Jian，Yan Yunhui，Guo Xinghui，et al. On-line control of strip surface quality for a continuous hot-dip galvanizing line based on inherent property of thin plate[J]. Journal of Mechanical Engineering，2011，47(9)：60-65(in Chinese).

［17］ 欧珠光. 工程振动[M]. 武汉：武汉大学出版社，2010.

Ou Zhuguang. Engineering Vibration[M]. Wuhan：Wuhan University Press，2010(in Chinese).

［18］ 刘习军，贾启芬. 工程振动理论与测试技术[M]. 北京：高等教育出版社，2004.

Liu Xijun，Jia Qifen. Engineering Vibration Theory andMeasurement Technology[M]. Beijing：Higher Education Press，2004(in Chinese).

［19］ 曾 攀，雷丽萍，方 刚. 基于ANSYS平台有限元分析手册——结构的建模与分析[M]. 北京：机械工业出版社，2011.

Zeng Pan，Lei Liping，Fang Gang. Structure Modeling and Analysis，Manual of FEA Based on ANSYS Platform[M]. Beijing：China Machine Press，2011(in Chinese).

［20］ 刘前勇. 2,180,mm六辊冷连轧机振动测试与仿真分析[D]. 北京：北京科技大学机械工程学院，2011.

Liu Qianyong. Vibration Measurement and Simulation of 2,180,mm Six-High Tandem Cold Rolling Mill [D]. Beijing：School of Mechanical Engineering，University of Science and Technology Beijing，2011(in Chinese).

［21］ 刘宏民，丁开荣，李兴东，等. 板形标准曲线的理论计算方法[J]. 机械工程学报，2008，44(8)：137-142.

Liu Hongmin，Ding Kairong，Li Xingdong，et al. Theoretical computational method of shape standard curve[J]. Journal of Mechanical Engineering，2008，44(8)：137-142(in Chinese).

［22］ 杜凤山，张尚斌，黄华贵，等. 六辊轧机刚度特性有限元[J]. 塑性工程学报，2010，17(3)：148-152.

Du Fengshan，Zhang Shangbin，Huang Huagui，et al. Finite element study of the rigidity characteristics of a six-high mill[J]. Journal of Plasticity Engineering，2010，17(3)：148-152(in Chinese).

［23］ 周晓敏，张清东，王长松. 西门子平坦度检测系统在冷轧中的应用[J]. 上海金属，2003，25(2)：37-40.

Zhou Xiaomin，Zhang Qingdong，Wang Changsong. Application of Siemens flatness measurement system to cold rolling mill[J]. Shanghai Metal，2003，25(2)：37-40(in Chinese).

(责任编辑：樊素英)

Setting of Excitation Frequency of SI-FLAT Shapometer

Yang Guanghui1，Zhang Jie1，Cao Jianguo1，Huang Qiaobao1，Jia Shenghui2
(1. School of Mechanical Engineering，University of Science and Technology Beijing，Beijing 100083，China；2. Cold Rolling Plant，Wuhan Iron and Steel(Group) Corporation，Wuhan 430083，China)

SI-FLAT shapometer is a non-contacting industrial shapometer which was firstly used in domestic widestrip tandem cold rolling mills. It was found during production that excitation frequency was set as a fixed value for often rolled strips of different specifications and that excitation force only changed with tensile stress，which led to the unstable shape control of strip. Excitation frequency had a great influence on the detection precision of strip shape. Based on the analysis of production data，two basic principles were put forward，which are amplitude control principle and detection internal control principle. For analyzing and calculating thenatural frequency and amplitude of forced vibration of strip，the vibration simulation model was built by the finite element software ANSYS12.0. With the model，the influences of some factors，such as strip shape，width，thickness and tensile stress，on the fluctuation of natural frequency were analyzed. It was found that tensile stress and shape had great effects on the natural frequency of strip. Finally，the feasible project was put forward based on the amplitude control principle and the detection internal control principle. Through limiting the minimum tensile stress，the influence of shape on the measurement result could be reduced，and for controlling the minimum detection interval so as to improve the on-line shape，the excitation frequency should be adjusted according to the speed of strip.

cold rolled strip；flatness measurement；excitation frequency；amplitude；detection interval

TG333.71

A

0493-2137(2014)10-0871-08

10.11784/tdxbz201305009

2013-05-04；

2013-08-22.

北京高等学校青年英才计划资助项目(YETP0369).

杨光辉（1977— ），男，博士，副教授.

杨光辉，yanggh@ustb.edu.cn.