基于光学自由曲面的三维位移测量系统

房丰洲，万 宇，朱朋哲，程 颖

基于光学自由曲面的三维位移测量系统

房丰洲，万 宇，朱朋哲，程 颖

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

针对数控机床、多轴位移台等多轴系统位移检测中存在的检测方法复杂、测量费用高等问题，利用光学自由曲面具有极大的设计自由度，可简化系统结构、提高系统性能的特点，设计开发了一种基于光学自由曲面的非接触式三维位移测量系统，用于普通机床、多轴位移台等多轴系统位移精度检测．通过设计光学自由曲面基准件，搭建实验平台，建立测量系统的数学模型，完成了测量系统的标定实验、测量系统精度验证实验和三维位移测量实验．结果表明，该测量系统精度达2.8,µm，可用于多轴系统的位移检测．

光学自由曲面；三维位移测量；数学模型标定；多轴系统

超精密三维位移测量技术一直是测量技术领域研究的热点，被广泛应用于工业自动化加工和工业检测等诸多工业场合．测量方法分为接触测量和非接触测量．其中接触测量(如接触式三坐标测量机、原子力显微镜、轮廓仪[1-2]等)一般只用于对工件表面形貌的测量；触针式光电三维微位移测量系统[3]主要用于一维位移的测量；而二维位移的测量是利用位移台的高精度定位实现，系统稳定性较差，且不适合对数控机床的测量；用球杆仪(DDB)测量机床误差已比较成熟，但该方法一般只适用于对动态误差、直线轴的直线度误差和垂直度误差的测量，即使结合其他高精度三维测头[4]或根据测量需要建立合适的数控机床误差模型[5]或结合基于激光干涉仪的12线法[6]，不仅无法测量机床的所有几何误差项，而且测量成本高．非接触测量通常采用视觉测量方法和光学测量方法实现三维测量，如双目或单目视觉[7-11]，虽然测量速度快，使用简单，可以测量形貌复杂的曲面或微位移量[12]，但其测量系统庞大、开发复杂、不便携带，且对测量环境有较高要求，不能随意用于工业现场，比如对机床、多轴位移台等多轴装置位移精度的检测．普通数控机床的精度在几微米到十几微米之间[13]，光学测量方法，如基于PSD的激光三角测距仪[14]，虽然精度受限，但符合普通机床的精度要求，且结构简单，可实现现场测量．目前市场上除了激光干涉仪之外还没有用于机床、多轴位移台等多轴装置位移精度检测[15-16]的非接触式测量方法．而激光干涉仪成本高昂，一般企业难以支付如此昂贵的测量费用．

光学自由曲面[17-18]是可实现光学性能的复杂形面，是新一代的光学元件．近年来，随着光学自由曲面设计和制造技术的发展，光学自由曲面在成像、照明、测量等各个领域得到了广泛的应用，尤其是在测量领域，利用双正弦自由曲面可实现二维位移的高精度测量[19-21]，测量精度可达纳米级，但利用双正弦自由曲面作为位移测量基准件引入了非线性误差，甚至存在测量灵敏度为零的区域．

笔者通过对光学自由曲面的优化，设计了一种基于光学自由曲面基准件的非接触式三维位移测量系统，测量精度达微米级，可实现对普通机床、多轴位移台等多轴装置的三维位移检测．

1 测量系统原理

1.1 系统工作原理

基于光学自由曲面的三维位移测量系统由光学自由曲面基准件、半导体激光器、光学准直缩束系统、偏振分光棱镜(PBS)、1/4波片、成像透镜、四象限光电二极管(QPD)、图像传感器(CCD)组成，如图1所示．激光器发出的光束经透镜组准直缩束成为直径200,µm的细直平行光束，P偏振光透过偏振分光棱镜(PBS)，再经1/4波片成为圆偏振光投射到光学自由曲面基准件上，反射光经1/4波片成为S偏振光，经偏振分光棱镜(PBS)反射再由透镜1会聚到四象限光电二极管(QPD)上．

当光学自由曲面基准件沿x或y轴移动时，光学自由曲面基准件上激光投射点处的斜率随之变化，根据反射定律，其成像光斑在四象限光电二极管(QPD)上的位置也发生相应改变，光斑在四象限光电二极管(QPD)上的位置和光斑投射在光学自由曲面基准件上的位置有一一对应的关系，从而实现x和y向位移的测量．类似地，光学自由曲面基准件上激光光斑投射点处的散射光经成像透镜成像到CCD上，当光学自由曲面基准件产生z向位移时，成像到CCD上的光斑位置随之变化，且两者之间一一对应，从而实现z向位移的测量．所搭建的测量系统实验装置如图2所示．

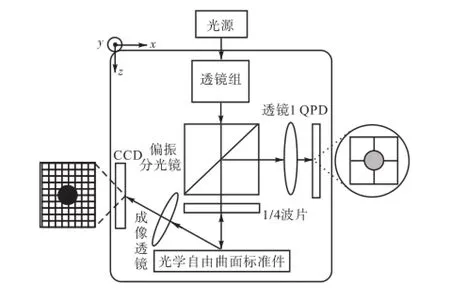
图1 系统原理Fig.1 Schematic diagram of the system

图2 实验装置实物Fig.2 Photo of experimental system in laboratory

1.2 光学自由曲面基准件

光学自由曲面基准件是三维位移测量系统的主要组成部分，本文通过对光学自由曲面的优化设计，选择以下两种光学自由曲面作为实现三维位移测量的基准．

1.2.1 双正弦自由曲面测量基准件

如图3所示的双正弦自由曲面，x和y方向的幅值和波长分别用xA、yA和xλ、yλ表示．

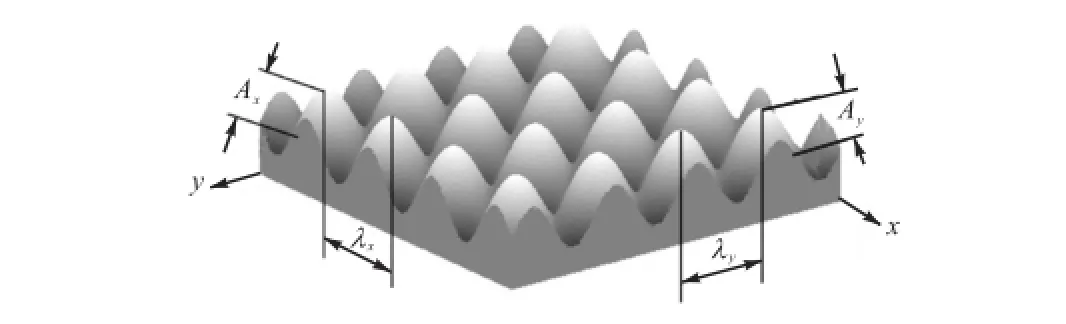
图3 双正弦自由曲面三维模型Fig.3Three-dimensional model of double sine free-form surface

双正弦自由曲面表面形貌特征[22]可表述为

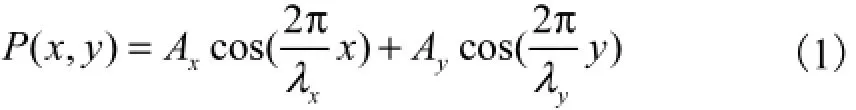
对式(1)分别在x、y方向求导，得到双正弦自由曲面各点斜率如式(2)和式(3)所示．

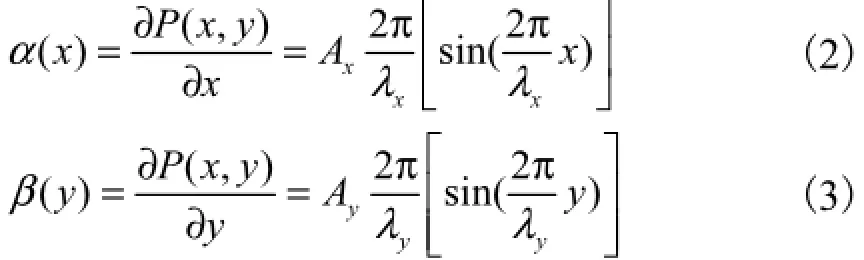
由此得到双正弦自由曲面上各点斜率是对应坐标值的正弦函数，通过测量被测点的斜率可以求得被测点的坐标，如果测量点间存在多个周期，可通过计入多个波长的距离，计算两测量点之间距离．

对式(1)求二阶导，得到双正弦自由曲面斜率变化率如式(4)和式(5)所示．

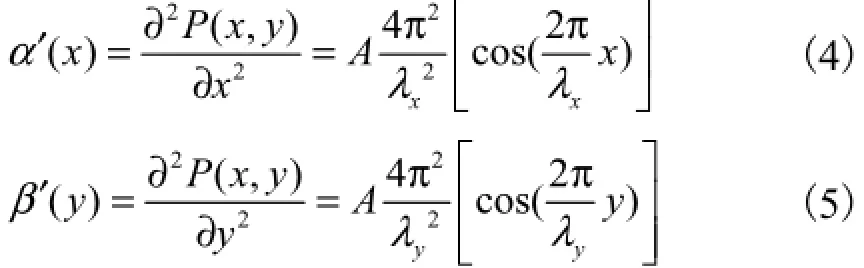
可见双正弦自由曲面的斜率变化率是其面形上各点坐标位置的余弦函数，由于测量系统x和y方向测量灵敏度与光学自由曲面基准件上各点斜率变化率呈线性关系，所以使用双正弦自由曲面作为三维位移测量基准件，则测量系统x和y方向测量灵敏度分别为

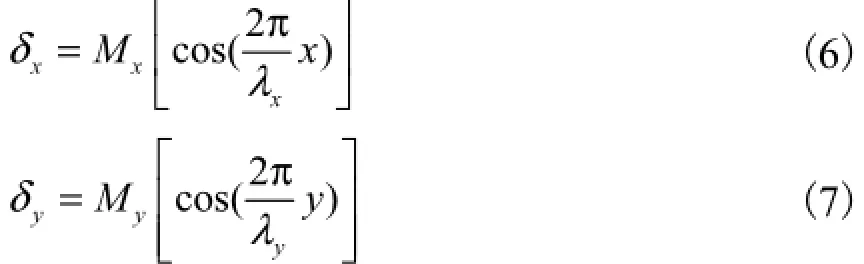
式中：δx、δy分别为x和y方向测量灵敏度；Mx、My为比例常数．从式(6)、式(7)得出，测量系统的测量灵敏度是双正弦自由曲面上各点坐标位置的余弦函数，这会增大测量系统的非线性误差，是测量准则中应该避免的．

双正弦自由曲面具有周期连续、口径大、加工简单的优点，但会增大测量系统的非线性误差，所以本文又设计了另一种光学自由曲面基准件——旋转抛物面．

1.2.2 旋转抛物面测量基准件

图4所示为旋转抛物面的三维模型剖面图．该旋转抛物面形貌特征可表述为

式中：(x，y，z)为旋转抛物面上各点坐标；a为旋转抛物面特征参数．

图4 旋转抛物面三维模型Fig.4 Three-dimensional model of rotating paraboloid surface

对式(8)分别在x和y方向求导，得到旋转抛物面各点斜率如下：

从式(9)、式(10)得出旋转抛物面各点斜率与其坐标位置有一一对应的线性关系．对式(8)求二阶导得

得出旋转抛物面斜率变化率为常数．由于测量系统x和y方向测量灵敏度与光学自由曲面基准件上各点斜率变化率呈线性关系，因此选取旋转抛物面作为三维位移测量标准件，测量系统x和y方向测量灵敏度为

式中M为常数．所以选用旋转抛物面作为光学自由曲面基准件使x和y方向位移的测量灵敏度为定值，消除了非线性误差．

利用光学设计软件Lighttools对x和y方向位移测量系统仿真，在满足测量精度的条件下扩大量程，仿真得到旋转抛物面曲率为0.005(a=20)，口径5,mm较为合适．图5所示为实际加工的旋转抛物面，在旋转抛物面边缘加工宽度2.5,mm的圆环平面，测量时可用于激光束和光学自由曲面基准件的垂直对准．

图5 旋转抛物面实物Fig.5 A photo of rotating paraboloid surface

为了分析旋转抛物面基准件的加工质量，使用泰勒公司PGI1250A轮廓仪对旋转抛物面进行测量．用二次曲线拟合形状误差数据，拟合结果如图6所示．

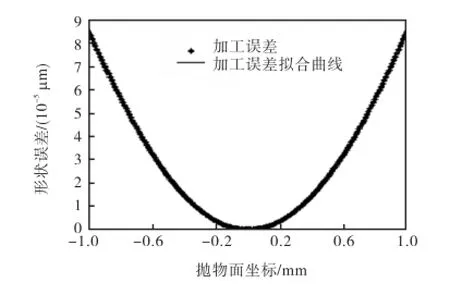
图6 轮廓仪测量结果Fig.6 Profilometer measurements

拟合曲线方程为

对式(14)求二阶导数，得到该拟合二次曲线方程的特征参数b =1.08×10-2．

由于测量系统的x和y方向位移测量模型方程与抛物面特征参数的二次方成正比，与旋转抛物面上被测点坐标位置呈线性关系(下一节会详细分析)，因此形状误差导致的测量误差为

式中：ε为形状误差导致的测量误差；b为加工误差拟合二次曲线方程的特征参数；x为旋转抛物面上的坐标值．旋转抛物面顶点为测量零点(四象限光电二极管(QPD)输出xout、yout为零的位置)，由于旋转抛物面的加工误差导致的最大测量误差为ε= ±0.084μm ，对测量系统精度影响较小，可以用作测量基准件．

由于测量系统可探测的斜率范围较小，因此使用单个抛物面测量量程小，如果想实现大量程的测量，需要采用图7所示的抛物面阵列．阵列中各抛物面和上文叙述设计的抛物面相同．受到单个抛物面量程的限制，抛物面口径设定为1.8,mm．采用单点金刚石车削的方法加工所示阵列，为确保加工精度，两抛物面间应有大于刀具刃口半径的间隔．综合考虑加工效率和加工精度，选用刃口半径为1.0,mm的刀具加工所示阵列，因此相邻两抛物面间隔确定为1,mm．由于已确定各抛物面面型和抛物面间的间距，所以阵列中各点坐标也唯一确定，当测量点间存在多个周期，可通过计入多个抛物面口径和抛物面间间隔，计算两测量点间距离．实际测量时，合适地选取被测多轴装置各运动轴位移量，确保各测量点始终在阵列中的抛物面上，记下测量系统x和y方向输出经历的周期数以及测量起始点和终止点的测量值，实现x和y方向位移的测量．根据测量量程的需要可改变阵列大小，实现x和y方向位移测量量程的自由选取.

图7 旋转抛物面阵列Fig.7 Array of rotating paraboloid surface

1.3 x、y方向位移测量

图8所示为激光自准直系统斜率探测原理示意．激光束经凸透镜会聚在四象限光电二极管(QPD)上，当激光束入射角变化时，光斑在四象限光电二极管(QPD)上的位置也相应改变．

图中Δθ为旋转抛物面被测点斜率倾角，f为凸透镜焦距，dy为光斑中心偏离四象限光电二极管中心的y向距离．由几何关系得

图8 激光自准直系统几何光学原理斜率探测示意Fig.8Schematic of geometrical optics slope detection of laser collimation system

由于四象限光电二极管可探测斜率范围较小，因此tan(Δθ)=Δθ，则式(16)可简化为

同理

因此通过四象限光电二极管(QPD)对光斑位置的探测，可实现对旋转抛物面上被测点斜率的测量，进而计算被测点坐标，得到两测量点之间x、y方向位移的大小．

通过理论计算，四象限光电二极管x、y方向测量值输出为

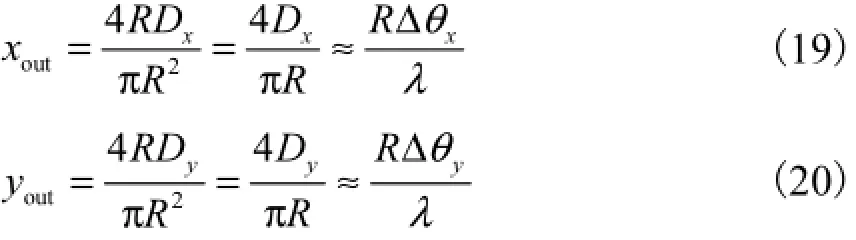
式中R、D和λ分别为四象限光电二极管(QPD)上光斑半径、入射光直径和激光波长．

因此得到

由于Δθx=α(x)，Δθy=α(y)，因此带入式(9)、式(10)，求得抛物面基准件上被测点坐标为

图9为x和y方向位移测量原理流程．

图9 x和y方向位移测量原理流程Fig.9 Flow chart of x and y direction displacement measurement

1.4 z方向位移测量

激光三角法[23]作为光电检测技术的一种，具有结构简单、测试速度快、实时处理能力强等优点，在长度、距离以及三维形貌等检测中有着广泛的应用．鉴于激光三角法的以上特点，z方向位移测量采用激光三角法实现．

实验选用美国MTI公司的型号为LTC-025-04的激光三角测距仪实现z方向位移测量，该测距仪各项参数如表1所示．

表1 激光三角测距仪各项参数Tab.1 Parameters of laser triangulation rangefinder

2 测量模型标定及测量实验

测量模型标定及测量实验都是基于单个抛物面基准件进行的．

2.1 测量模型标定

式(23)和式(24)中l、f和a均为已知量，但实验装置台搭建过程中由于多种因素的影响会导致l、f和a的实际值与理论值不一致，因此不能用理论设计值求解测量模型方程，有必要对x和y方向位移测量模型进行标定．z方向位移测量选用了美国MTI公司的激光三角测距仪，因此不必标定z方向测量．

目前一般采用曲线拟合的方法标定式(23)和式(24)所示的测量模型，具体方法有平移端点法、最小二乘直线法、分段直线法、高次多项式法等[24]．

平移端点法及最小二乘直线法必须在测试系统的最大相对不确定度非常小的条件下才能使用．分段直线法的应用条件不仅要求系统的最大相对不确定度非常小，而且标定出的波形有锯齿形，棱角比较多，很不光滑．

在水利工程建筑材料方面，安排了喷涂高抗冲磨、混凝土养护、高性能化学灌浆、高密度阳离子聚合物、纳米塑料合金等工程建筑材料的技术；研制了一批性能优异，施工便利的高性能建筑材料，并在新安江水电站、龙滩水利水电工程及南水北调中线工程中得到成功运用；促进了我国建筑材料防护性能的提升，提高了我国建筑材料的环保性能，为建设环境友好型水利工程提供了支撑。

为了尽量减小标定对测量系统引入的误差，用高次多项式拟合法标定该三维位移测量系统的x和y方向位移测量模型．标定过程如下：利用定位精度为1,µm的三维位移台为基准位移台，旋转抛物面基准件固定在该位移台上，基准件在位移台的驱动下分别在x和y方向以10,µm为间隔移动，测量系统在全量程范围内测量基准件位移，得到多个测量点的信息(ix，iy)，其中ix、iy分别表示第i个测量点测量系统的输出值和位移真值．为降低拟合误差，一般取已知点的个数大于待定系数的个数，故设定m个测量点(m＞k+1，k为多项式拟合的最高次数)．多项式拟合方法如下所述．

对于任意的变量y和x，y可表示为

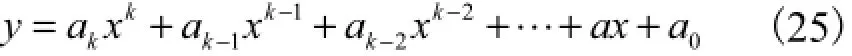
因此矩阵Y为

求得系数矩阵A为

系统的估计误差平均值为

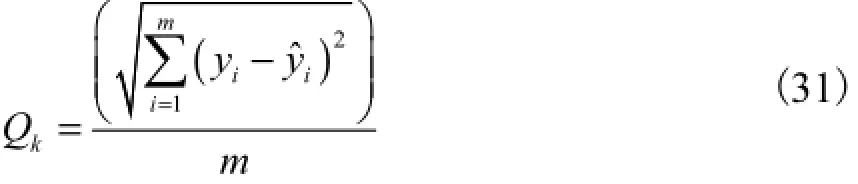
式中：ka、1ka-、…、0a为拟合多项式各阶次项系数；N、A和Y分别为拟合方程中测量点的测量值矩阵、系数矩阵和测量点位移真值矩阵；kQ为系统估计误差平均值；ˆiy为通过拟合方程求得的第i个测量点位移．

为了分析测量系统自身不稳定性产生的最大测量误差，分别在6个测量点进行了5次重复测量．测量结果如图10所示，图中6条曲线分别表示6个不同测量点5次重复测量的结果，经过误差分析得到本系统x和y方向位移测量的最大误差为±2.8,µm．

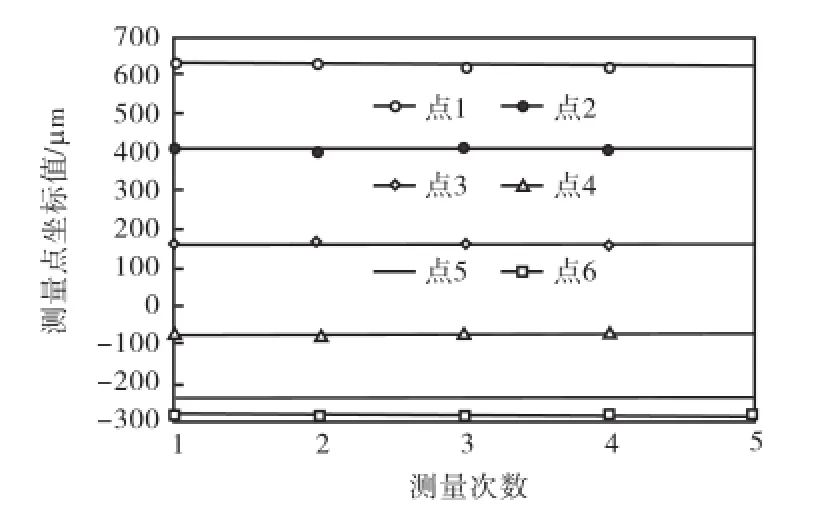
图10 多次重复测量曲线Fig.10 Repeated measurement curve

为简化计算，在满足拟合要求的同时，尽可能降低多项式阶数，k应选取在满足Qk≤2.8μm 时拟合方程的最小次数．通过对数据点的拟合计算得出当k= 7时即可满足要求，因此用7次多项式拟合x和y方向测量的数学模型方程．x和y方向拟合曲线以及测量点拟合值与真实值的偏差曲线如图11所示．

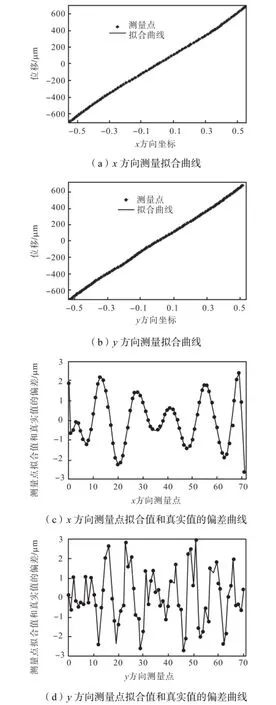
图11 x和y方向拟合曲线以及测量点拟合值与实际值的偏差曲线Fig.11 Fitting curves of x and y direction measurement and the curve of the error between fitted values and the true value of x，y direction measurement

在实验过程中发现，受到四象限光电二极管(QPD)探测特性的影响，当光斑中心偏离四象限光电二极管(QPD)中心的距离较大时，四象限光电二极管(QPD)非线性输出严重．经过多次实验，舍去测量系统的非线性测量区域，得到单个抛物面的测量量程为1.8,mm．

2.2 测量系统测量精度验证实验

标定完该三维位移测量系统后，需使用更高精度的位移系统来检验该测量系统标定结果的正确性和测量的准确性．本次使用的基准位移台是定位误差为1,nm的nanotech 250,UPL车床．由于nanotech 250,UPL车床不具备y轴，因此只能实现对该测量系统的x方向位移测量的误差分析．x和y方向位移测量具有相同的原理，共用同一光路系统和探测器件，所以x和y方向位移测量的误差表现形式基本相同．因此，只需分析x方向位移测量精度即可获得y方向位移测量精度．

分析该次测量结果，各测量点的测量误差如图12所示，x和y方向位移测量的最大误差为2.7,µm，且测量误差集中分布在-2.0～2.0,µm范围内．

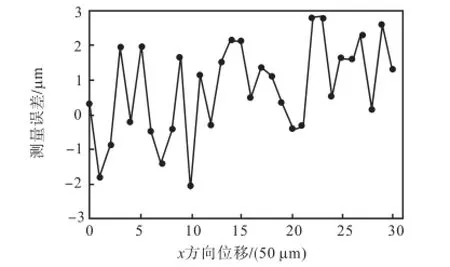
图12 测量系统精度验证实验Fig.12 Measuring system accuracy verification experiment

该三维位移测量系统采用四象限光电二极管(QPD)作为传感器件，所以它的精度直接决定了测量系统的精度．四象限光电二极管(QPD)的测量精度主要受背景光和暗电流的影响．

背景光的影响采用了补偿的方法予以降低，但是暗电流却很难消除．x和y方向位移测量的数学模型要求四象限光电二极管(QPD)感光平面和成像透镜主平面平行，但由于安装误差的存在，无法保证上述分析中的几何关系，这也是产生测量误差的主要原因之一．

2.3 三维位移测量实验

在完成了x和y方向位移测量的标定实验、x和y方向位移测量精度验证实验后，结合激光三角测距仪，实现三维位移测量．如图13所示，实验时将旋转抛物面固定在定位精度为1,µm的三维位移台上，将抛物面的斜率零点(四象限光电二极管(QPD)输出xout、yout为零的位置)设为坐标零点，通过三维位移台三维移动确定被测点坐标真值，再利用本测量系统对任意给定点的坐标位置进行测量．测量误差曲线如图14所示．

图13 三维位移测量实验Fig.13 Photo of of three-dimensional displacement measurement experiments

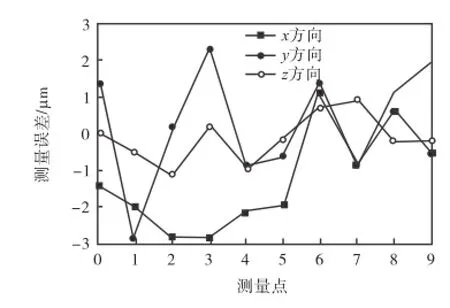
图14 三维位移测量误差曲线Fig.14 Error curve of three-dimensional displacement measurement

实验使用美国MTI公司的激光三角测距仪实现z方向位移测量，得到z方向位移误差分布在±1,µm以内，测量结果符合实验中使用的位移台的精度标准．x和y方向位移测量误差分布在±2.9,µm以内．

3 结 语

本文设计了一种基于光学自由曲面的三维位移测量系统．通过设计光学自由曲面基准件，并完成相关实验，得到该测量系统的最高精度可达2.8,µm，并可用于三维位移测量．配以相应的误差辨识手段，该测量系统可实现普通机床、位移台等多轴装置误差检测，相较现有的多轴装置误差测量手段，该测量系统成本低廉，具有很好的推广和使用价值．

参考文献：

［1］ 刘祚时，倪潇娟. 三坐标测量机(CMM)的现状和发展趋势[J]. 机械制造，2004，42(8)：33-34．

Liu Zuoshi，Ni Xiaojuan. Present state and developing trend of three-coordinate measuring machines[J]. Machinery，2004，42(8)：33-34(in Chinese).

［2］ Küng A，Meli F，Thalmann R. Ultraprecision micro-CMM using a low force 3D touch probe[J]. Measurement Science and Technology，2007，18(2)：319-327.

［3］ 于唤唤，张宏伟，张晓杰，等. 触针式光电三维微位移测量系统设计及标定[J]. 电子测量与仪器学报，2012，26(7)：616-623.

Yu Huanhuan，Zhang Hongwei，Zhang Xiaojie，et al. Design and calibration of three-dimensional microdisplacement measuring system with photoelectric stylus [J]. Journal of Electronic Measurement and Instrument，2012，26(7)：616-623(in Chinese).

［4］ Lei W T，Hsu Y Y. Accuracy test of five-axis CNC machine tool with 3D probe-ball(Part Ⅰ)：Design and modeling[J]. International Journal of Machine Tools and Manufacture，2002，42(10)：1153-1162.

［5］ Jiang L，Ding G，Li Z，et al. Geometric error model and measuring method based on worktable for five-axis machine tools[J]. Proceedings of the Institution of Mechanical Engineers(Part B)：Journal of Engineering Manufacture，2013，227(1)：32-44.

［6］ Zhu S，Ding G，Qin S，et al. Integrated geometric error modeling，identification and compensation of CNC machine tools[J]. International Journal of Machine Tools and Manufacture，2012，52(1)：24-29.

［7］ Su X，Zhang Q. Dynamic 3-D shape measurement method：A review[J]. Optics and Lasers in Engineering，2010，48(2)：191-204.

［8］ 袁 勇，吴禄慎，潘俊伟. 基于三维测量技术的相移微动装置研究[J]. 南昌大学学报：工科版，2003，25(2)：10-13.

Yuan Yong，Wu Lushen，Pan Junwei. The study of phase- shift micro-movement device based on 3D measuring technique[J]. Journal of Nanchang University：Engineering and Technology，2003，25(2)：10-13(in Chinese).

［9］ 毛先富，苏显渝，向立群，等. 基于手持相位标靶技术的光学三维坐标测量[J]. 光学学报，2010，30(7)：2006-2011.

Mao Xianfu，Su Xianyu，Xiang Liqun，et al. Optical 3D coordinate measurement based on handheld phase target [J]. Acta Optica Sinica，2010，30(7)：2006-2011(in Chinese).

［10］ Helfrick M N，Niezrecki C，Avitabile P，et al. 3D digital image correlation methods for full-field vibration measurement[J]. Mechanical Systems and Signal Processing，2011，25(3)：917-927.

［11］ 孙 伟，何小元，Quan C，等. 基于数字图像相关的三维刚体位移测量方法[J]. 光学学报，2008，28(5)：894-901.

Sun Wei，He Xiaoyuan，Quan Chenggen，et al. Threedimensional rigid body displacement measurement based on digital image correlation[J]. Acta Optica Sinica，2008，28(5)：894-901(in Chinese).

［12］ 赵 新，郭春艳，张玮光，等. 基于显微图像处理的MEMS 运动测量方法[J]. 纳米技术与精密工程，2012，10(1)：1-5.

Zhao Xin，Guo Chunyan，Zhang Weiguang，et al. Motion measurement method of MEMS based on microimage processing[J]. Nanotechnology and Precision Engineering，2012，10(1)：1-5(in Chinese).

［13］ 林 宋，张超英，陈世乐，等. 现代数控机床[M].北京：化学工业出版社，2011.

Lin Song，Zhang Chaoying，Chen Shile，et al. Modern CNC Machine Tools [M]. Beijing：Chemical Industry Press，2011(in Chinese).

［14］ 宋殿友，刘铁根，丁小昆，等. 精密PSD微位移在线测量系统[J]. 天津大学学报：自然科学与工程技术版，2013，46(2)：168-173.

Song Dianyou，Liu Tiegen，Ding Xiaokun，et al. Precise PSD micro-displacement online measurement system[J]. Journal of Tianjin University：Science and Technology，2013，46(2)：168-173(in Chinese).

［15］ 王跃明. 空间误差补偿技术在数控机床上的应用[J].制造技术与机床，2013(1)：45-48.

Wang Yueming. Application of volumetric error compensation on CNC machine tool [J]. Manufacturing Technology & Machine Tool，2013(1)：45-48(in Chinese).

［16］ 洪迈生，苏 恒，熊诗波，等. 数控机床运动误差检测技术(待续)[J]. 组合机床与自动化加工技术，2002(1)：18-20，23.

Hong Maisheng，Su Heng，Xiong Shibo，et al. CNC machine error motion measurement review[J]. Modular Machine tools & Automatic Manufacturing Technique， 2002 (1)：18-20，23(in Chinese).

［17］ 王涌天. 自由曲面光学系统设计及其应用[J]. 光学与光电技术，2012，10(3)：13-15.

Wang Yongtian. Design and application of free-curved surface optical system [J]. Optics & Optoelectronic Technology，2012，10(3)：13-15(in Chinese).

［18］ Zheng Zhenrong，Hao Xiang，Liu Xu. Freeform surface lens for LED uniform illumination[J]. Applied Optics，2009，48(35)：6627-6634.

［19］ Gao W，Dejima S，Shimizu Y，et al. Precision measurement of two-axis positions and tilt motions using a surface encoder[J]. CIRP Annals-Manufacturing Technology，2003，52(1)：435-438.

［20］ Gao W，Araki T，Kiyono S，et al. Precision nanofabrication and evaluation of a large area sinusoidal grid surface for a surface encoder[J]. Precision Engineering，2003，27(3)：289-298.

［21］ Gao W，Kimura A. A three-axis displacement sensor with nanometric resolution[J]. CIRP Annals-Manufacturing Technology，2007，56(1)：529-532.

［22］ Gao Wei，Saito Yusuke，Sato Hayato，et al. Development of a sensitive two-axis micro-angle sensor[J]. Journal of the Japan Society for Precision Engineering(CD-ROM)，2006，72(9)：1174-1178.

［23］ 王晓嘉，高 隽，王 磊. 激光三角法综述[J]. 仪器仪表学报，2004，25(4)：601-604.

Wang Xiaojia，Gao Jun，Wang Lei. Survey on the laser triangulation [J]. Chinese Journal of Scientific Instrument，2004，25(4)：601-604(in Chinese).

［24］ 何晓兰，姜国权，杜尚丰. 基于多项式拟合的摄像机标定算法[J]. 中南大学学报：自然科学版，2007，38(增1)：1117-1122.

He Xiaolan，Jiang Guoquan，Du Shangfeng. Camera calibration arithmetic based on integration of multinomial [J]. Journal of Central South University：Science and Technology，2007，38(Suppl 1)：1117-1122(in Chinese).

(责任编辑：赵艳静)

Three-Dimensional Displacement Measurement System Based on Optical Free-Form Surface

Fang Fengzhou，Wan Yu，Zhu Pengzhe，Cheng Ying
(State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China)

In the displacement measurement of multi-axis systems such as computer numerical control(CNC)machine tools and multi-axis translation stages，there exist many problems. For example，the detection methods are complicated and the cost is high. Regarding these problems，full use was made of the advantages of great design freedomof optical freeform surface to simplify the system and improve system performance. A method of non-contact threedimensional displacement measurement based on an optical free-form surface was proposed to detect the accuracy of multi-axis systems such as general CNC machine tools. The optical free-form surface used as datum was designed. The experimental platform was built and the mathematical model of measurement system was established. Then，the system was calibrated and its accuracy was tested. Finally，three-dimensional displacement measurement experiments were carried out. Results show that the accuracy of the measurement system was up to 2.8,µm，and the measurement system can be applied to the three-dimensional displacement measurement of multi-axis systems.

optical free-form surface；three-dimensional displacement measurement；mathematical model calibration；multi-axis systems

TK448.21

A

0493-2137(2014)10-0934-09

10.11784/tdxbz201306055

2013-06-25；

2013-11-18.

国家重点基础研究发展计划(973计划)资助项目(2011CB706703).

房丰洲（1963— ），男，长江学者特聘教授，博士生导师，fzfang@gmail.com.

朱朋哲，pengzhezhu@gmail.com.

时间：2014-01-07.

http：//www.cnki.net/kcms/detail/12.1127.N.20140107.0900.001.html.