基于CAD模型的三坐标测量机测量点分布规划
张 虎,张 润,于连栋
(合肥工业大学 仪器科学与光电工程学院,合肥230009)
三坐标测量机CMM 是一款新型坐标测量仪器,具有测量精度高、通用性强、高效便捷等优点,广泛应用于机械制造、飞机装配和航天航空等工业领域[1]。 针对三坐标测量的使用,在传统的测量中,对单个对象或者零件的测量路径往往是根据人工经验所得, 测量路径和测量时间往往都不是最佳的。 然而,测量路径和测量时间影响着测量的效率和智能化水平,因此智能化三坐标测量机是未来的发展趋势。智能化三坐标测量机根据CAD 模型自动生成测量方案[2],减少人力的干预,提高测量效率。
文献[3]按照测量点之间的最短距离原则,确定每个测量面内测量点的先后测量顺序,并按照此顺序来生成测量路径;文献[4]提出了平面、圆柱面和圆锥面上的测量点均匀分布方式和基于CMM 的检测路径规划;文献[5]根据常见机械零件的特征,阐述了一种最优路径测量规划方法;文献[6]针对一般表面的采样点分布不足,提出一种步长自适应再分的采样方法;文献[7]研究了零件模型的特征提取和识别,得出测量点的分布,形成有效的测量方案;文献[8]提出了一种基于蚁群算法测量棱镜物体的三坐标测量路径方法。 这此研究为测量加工系统的一体化提供了丰富的经验。
在此,根据以上所构建的良好基础和宝贵的思想,同时基于OpenCasCade 的边界表示法BRep(boundary representation),研究了三坐标测量机测量策略软件界面的规划和一般多边形平面、圆柱面和自由曲面的模型元素识别和测量点分布;根据不同的CAD 模型试验验证了软件系统的可行性。
1 IGES文件的读取和特征识别
IGES 是一种特定的文件结构的数据结构,且目前大部分CAD 系统软件都使用IGES 数据接口标准。 因此,不同的CAD 系统之间使用IGES 文件进行文件格式转换和文件共享十分方便。
1.1 IGES 规范
IGES 文件包括固定长ASCII 码、压缩的ASCII码和二进制等3 种形式。其中,固定长ASCII 码是最常见的,其IGES 文件每行有80 个字符,整个文件可以分为5 段:开始断、全局段、元素索引段、参数数据段和结束段[9]。
1.2 读取IGES 文件
三坐标测量机测量策略软件界面的规划通过开发环境Visual Studio 2010,软件整体界面如图1所示。 通过Opencascade 对CAD 模型数据进行读取的部分代码如下:

图1 三坐标测量机测量策略软件界面Fig.1 CMM measurement strategy software interface
2 CAD 模型的特征识别
CAD 模型中包含了零件详细的数据,但是不能在算法中直接使用, 需要通过边界表示法BRep 获取模型的几何信息和拓扑信息。 在BRep 中按照“体—面—环—边—点”的层次,记录构成模型的所有几何元素的几何信息及其相互连接的拓朴关系。针对一个模型,结构层次中“体—面—环—边”识别效果如图2 所示。 特征识别的大致过程如下:
步骤1 将IGES 格式的CAD 模型转换为需要的拓扑信息;
步骤2 基于每个拓扑实体几何特征确定其类型;
步骤3 不同的几何类型保存于不同的数据链表中,为后期的算法使用方便。

图2 对“体-面-环-边”的识别效果Fig.2 Result of identification for “body-face-loop-line”
3 曲面测量点分布策略
获得自由曲面表面的测量点分布,分为一般平面、圆柱圆柱面和复杂曲面等3 种方式进行研究。
3.1 一般平面
步骤1 在内存中新建测量点的数据结构栈。
步骤2 根据从CAD 模型中选取的表面获取其拓扑信息。 拓朴信息中包含了CAD 模型的顶点、边、面的连接关系,形成物体边界表示的“骨架”,并从拓扑信息中获得测量表面的顶点和环的几何信息。环是相接面上的边界部分,由有向边组成。环分为外环和内环,外环即面的最外层与相接面连接的部分,内环即面的内部与相接面连接的部分。
步骤3 求出顶点的相邻两条边的角平分线和平面的单位法向量。
步骤4 求出以顶点的相邻两条边中较短的一条边的一半为半径,顶点为圆心的圆面。
步骤5 步骤2 的角平分线和步骤3 的圆面所相交的点即为其中一个测量点,存入栈中,依次重复第2 个顶点,转至步骤3,直到所有的顶点相对应的测量点。
步骤6 求出所得测量点顶点是否在步骤1 所求的内环的外部,如果测量点在内环的内部(即所得测量点不在测量表面内),转至步骤4,同时减小步骤4 中半径为原来的1/2。 求出所有的测量点然后结束。
一般平面测量点分布原理如图3 所示。 根据顶点P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3),求 出测量点P2′(x2′,y2′,z2′)为
式中:n 为表面 的法 向量;θ1为的夹角;θ2为的夹角。
可以求得2 个点, 其中一个点在面外可以舍去,另外一个点即为所求的测量点。
3.2 圆柱圆锥面
在对圆柱面和圆锥面选取并确定参数时,由于OpenCasCade 中拓扑结构的关系, 只能选取完整参数表面的一部分,因此需要对选取的部分表面进行拼接[10],其过程如图4 所示。
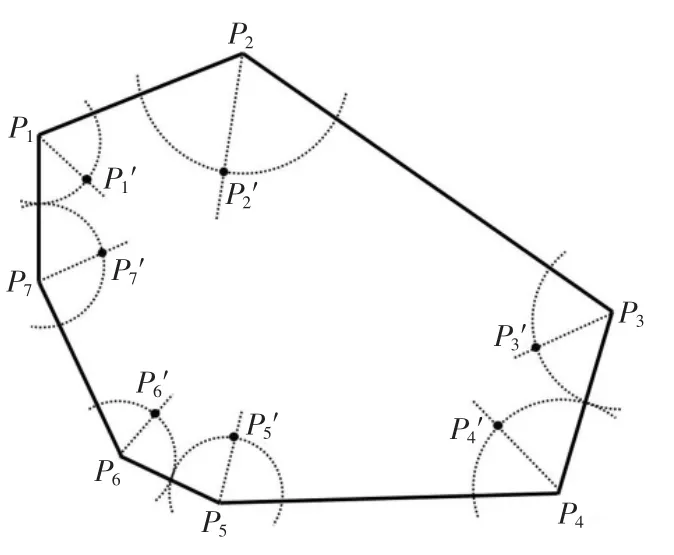
图3 一般平面测量点分布的原理Fig.3 Schematic of general plane peasurement point distribution
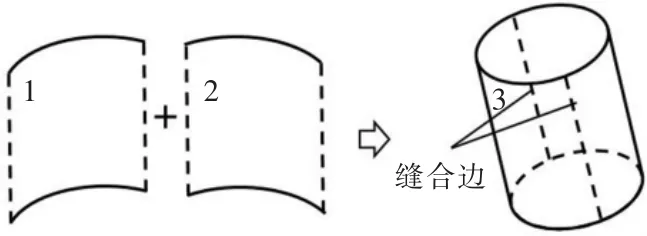
图4 圆柱面的拼接过程Fig.4 Process of cylindrical splicing
圆柱和圆锥的拼接步骤如下:
步骤1 选取与圆柱面垂直且相交的平面,计算其法向量;
步骤2 根据选取的表面1 和表面2 的拓扑结构进行遍历,获取其所有的顶点数据;
步骤3 步骤2 中所有的顶点依次与步骤1 中选取的平面中任意2 点 (保证3 点不在一条直线上),计算其3 点组成平面的法向量,如果与步骤1中平面的法向量平行即为圆柱体底面圆中的2 点;
步骤4 根据计算出顶点的位置关系, 构造出一个完整的圆柱面。
对于圆柱面和圆锥面中,测量圆的高度为
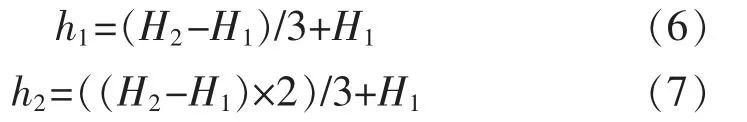
式中:H2和H1分别为圆柱圆锥面的上底面、下底面高度;h1和h2为测量点的高度。
分别在2 个圆上按照对称性在其上生成4 个测量点,这样在圆柱面或者圆锥面表面共有8 个测量点。
3.3 自由曲面
在几何造型内核OpenCascade 中, 采用参数表示法来表示参数曲面。参数曲面的表示是由参数u和v 组成的向量函数P(u,v)=(x(u,v),y(u,v),z(u,v)),其中:u∈[umin,umax],v∈[vmin,vmax]。参数u,v 表示uv平面上的一个矩形区域,当一个参数不变时,如v=v0,那么p(u,v0)为曲面上的一条曲线,即为等参线,如图5 所示。
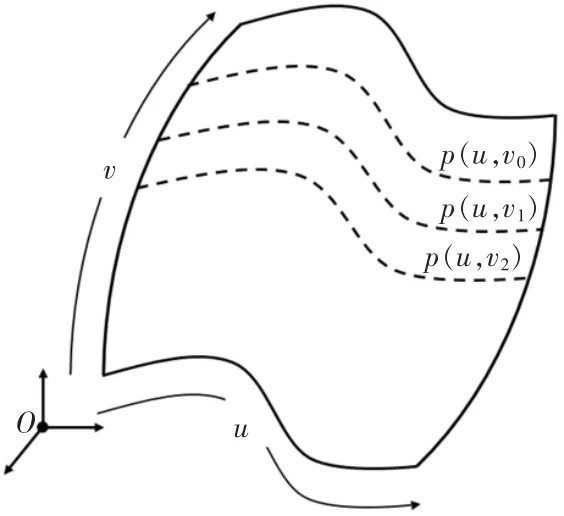
图5 自由曲面等参线Fig.5 Isoparametric line of free-form surface
对于曲面的测量,基于“面—线—点”的测量点分布的思路[11]。先求出曲面的等参线,再从等参线上根据曲率的变化求出测量点分布。 实现过程如下:
步骤1 在曲线p(u,v0)上设置测量的初始点p0(u0,v0)和测量点间距的固定值d;
步骤2 使u1=u0+d,同时所得点p1(u1,v0)为第2 个测量点;
步骤3 求出测量点p0和测量点p1在曲线p(u,v0)上曲率k0和k1的比值K,K=k1/k0,则
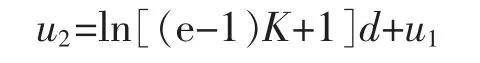
点p2(u2,v0)为第3 个测量点,直至u>umax。
步骤4 直到求出同等间距等参线测量点。
4 试验验证
为验证三坐标测量机测量策略软件中一般平面、圆柱面和一般参数曲面的模型识别和测量点分布的的可行性和有效性,在三坐标测量机测量策略软件中导入文件类型IGES 的不同CAD 模型;通过特征识别,获取每个CAD 模型中测量点的坐标值和每个测量点的单位法向量。 法向量在测量系统的重要性是由于一个三维表面包含正面和背面,如果正面朝外,则背面一定在整个模型的内部,三坐标测量机的测头只有通过正面的法向量方向去接触测量点。 三坐标测量机测量分布规划实例如图6 所示。
图6(a)展示了对一般平面的测量点分布和单位法向量的结果,测量点的数量为6;图6(b)展示了对圆柱面的测量点分布和单位法向量的结果,并且在求得测量点的过程中存取了3 个面的信息数据,测量点的数量为8;图6(c)展示了自由曲面的测量点分布和单位法向量的结果,测量点的数量为95。

图6 三坐标测量机测量分布规划实例Fig.6 Example of distribution planning for CMM measurement
5 结语
研发了基于CAD 模型的三坐标测量机测量点分布策略与CAD 系统的集成。 在三坐标测量机测量策略软件中,展示了CAD 模型元素的特征识别、基于顶点角平分线分布方案的一般多边形平面测量点分布策略、圆柱面的拼接和测量点分布策略和基于曲率变化的自由曲面测量点动态分布策略; 可以提高测量的质量和效率,为实际中CAD 模型测量提供理论基础。 实例验证了测量点分布规划的可行性和有效性。

